Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закрепление изученного материала.
Тэо-21 тора-21 11.02.2022 Тема урока: «Возрастание и убывание функции». Цель:
o образовательная: изучить достаточные условия возрастания и убывания функций, научить применять понятие производной для нахождению промежутков монотонности функции; · развивающая: развитие навыков самоконтроля, внимательности; развитие мыслительной деятельности учащихся; · воспитательная: воспитание точности, аккуратности, уважению к труду одноклассников, ответственности за результаты своего труда и труда одноклассника. Что называется производной функции f(x) в точке x0? Производной функции f '(x) в точке x0 называется предел разностного отношения при h→0, т.е. f '(x0)= Чему равны производные постоянной функции, линейной функции, степенной функции? Производная постоянной функции с'=0. Производная линейной функции (kx+b)'=k. Производная степенной функции (хр)'=р*хр-1, pϵR, x>0. Сформулируйте правило дифференцирования суммы. (f(x)+g(x))'=f '(x)+g '(x). Сформулируйте правило дифференцирования произведения. (f(x)*g(x))'=f '(x)*g(x)+f(x)*g '(x). Сформулируйте правило дифференцирования частного.
(sin x)'; (cos x)'; (ln x)'; (ex)'; (tg x)'; (ctg x)'; (ln|x|)'; (ax)'; ( (sin x)'= cos x (cos x)'= –sin x (ln x)'= (ex)'=ех (tg x)'= (ctg x)'=– (ln|x|)'= (ax)'=ахln a, a>0, a≠1 ( (xp)'=pxp-1, pϵR, x>0.
Изучение нового материала. С помощью производной можно находить промежутки монотонности функции. Условимся термин «промежуток» использовать для обозначения таких числовых множеств, как отрезок [a;b], интервал (a;b), полуинтервалы [a;b) и (a;b]. При этом точки a и b называют граничными точками, а все остальные точки интервала (a;b)-внутренними точками промежутка. Функция f(x) называется возрастающей на некотором промежутке, если большему значению аргумента соответствует большее значение функции, т.е. для любых точек x1 и x2 из этого промежутка, таких, что x2>x1, выполняется неравенство f(x2)>f(x1). (Слайд 3) Если для любых точек х1 и х2 данного промежутка, таких, что х2>x1, выполняется неравенство f(x2)<f(x1), то функция f(x) называется убывающей на этом промежутке. Промежутки возрастания и убывания функции называются промежутками монотонности этой функции. Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда если f'(x)>0 для всех xϵ(a;b), то функция f(x) возрастает на отрезке [a;b], а если f'(x)<0, то она убывает на этом отрезке. Применяя определение возрастающей (убывающей) функции трудно найти промежутки монотонности, поэтому мы будем изучать признаки монотонности функции, использующие понятие производной. При доказательстве теорем о достаточных условиях возрастания или убывания функции используется следующая теорема, которая называется теоремой Лагранжа. Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует точка, такая cϵ(a;b), что f(b)–f(a)=f'(c)(b–a). ( Запись в тетрадях: f(b)–f(a)=f'(c)(b–a).(1) Эта теорема доказывается в курсе высшей математик. Поясним геометрический смысл формулы (1). Проведем прямую l (рис.56 из учебника) через точки A(a, f(a)) и B(b, f(b)) графика функции y=f(x) и назовем эту прямую секущей. Угловой коэффициент k секущей l равен
Равенство (1) можно записать в виде
Из равенства (2) и (3) следует, что угловой коэффициент Таким образом, на интервале (a;b) найдется такая точка c, что касательная к графику функции y=f(x) в точке C(c; f(c)) параллельна секущей l. Давайте запишем алгоритм нахождения промежутков возрастания и убывания 1. Находим производную функции. 2. Находим, при каком значении х, производная функции равна нулю. 3. Находим промежутки, на которые найденная точка разбивает ось Ох, и находим значение производной функции в какой - нибудь точке каждого из интервалов. 4. Находим промежутки возрастания и убывания функции. Давайте рассмотрим функцию f(x)=2х2+4х-4. Сначала находим производную этой функции. f '(x)= (2х2+4х-4)'=4x+4. Затем производную f'(x) приравниваем к нулю и находим значение х. f '(x)=0, т.е. 4х+4=0; х=-1. После этого отмечаем значение х на числовой оси и выясняем какие знаки будут на интервалах.
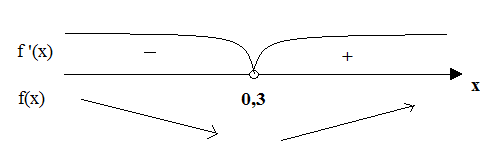
Делаем вывод: т.к. f '(x)>0 на интервале (-∞;-1), то функция f(x) - возрастает; а на интервале (-1; +∞) функция f(x) -убывает, т.к. f '(x)<0. Промежутки возрастания и убывания функции называются промежутками монотонности этой функции. При доказательстве теорем о достаточных условиях возрастания или убывания функции используется следующая теорема, которая называется теоремой Лагранжа. Прочитайте вслух первую теорему из учебника. Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует точка, такая cϵ(a;b), что f(b)–f(a)=f'(c)(b–a). Запись в тетрадях: f(b)–f(a)=f'(c)(b–a). Прочитайте нам вторую теорему. Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда если f'(x)>0 для всех xϵ(a;b), то функция f(x) возрастает на отрезке [a;b], а если f'(x)<0, то она убывает на этом отрезке. Какого вида функция f(x)=5x2-3x-1, является ли она сложной? Функция сложная, представляет собой сумму нескольких функций, значит найдем производные каждого из слагаемых f(x)=5x2-3x-1 f '(x)=(5x2-3x-1)'=(5x2)¢-(3x)¢-1¢=10x-3 Каков следующий шаг решения? Найдем ,при каком значении х, производная функции равна нулю: f '(x)=0; 10x-3=0; x=0,3.
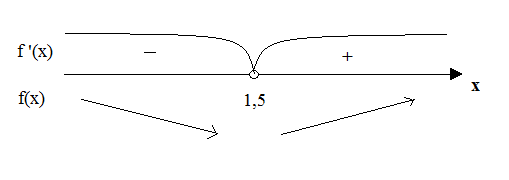
Определяем промежутки возрастания и убывания функции. Ответ: на интервале (-∞; 0,3) – функция f(x) – убывает, т.к. f '(x)<0; на интервале (0,3; +∞) – функция возрастает, т.к. f '(x)>0. Найти интервалы возрастания и убывания функции. (Запись в тетрадях). Решение: 1. f(x)=х2-3х+4 f '(x)=(х2-3х+4)'=2х-3 f '(x)=0; 2х-3 =0; х=1,5.
Ответ: на интервале (-∞; 1,5) – функция f(x) – убывает, т.к. f '(x)<0; на интервале (1,5; +∞) – функция возрастает, т.к. f '(x)>0.
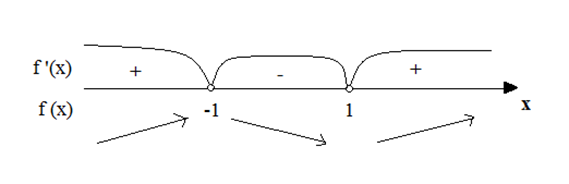
(Запись в тетрадях). 3) f(x)=х3-3х f '(x)=( х3-3х)'=3х2-3 f '(x)=0; 3х2-3=0; x1=-1; х2=1.
Ответ: на интервалах (-∞; -1) и (1; +∞) – функция f(x) – функция возрастает, т.к. f '(x)>0; на интервале (-1; 1) – функция убывает, т.к. f '(x)<0.
Домашнеее задание: Составить конспект. Выписать формулы Найти интервалы возрастания и убывания функции f(х) = Построить график функции f(х) = Найти наибольшее и наименьшее значения функции f(х)=
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 5; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.200.102 (0.008 с.) |
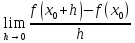 .
.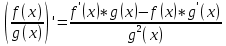 .Напишите производные элементарных функций.
.Напишите производные элементарных функций.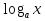 )'; (xp)'.
)'; (xp)'.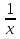 , х>0.
, х>0.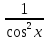 ,x≠
,x≠ 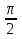 +kπ, kϵz.
+kπ, kϵz.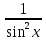 ,x≠kπ, kϵz.
,x≠kπ, kϵz.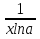 ,a>0, a≠1, x>0.
,a>0, a≠1, x>0.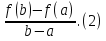
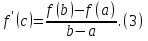
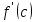 касательной к графику функции y=f(x) в точке C с абсциссой c равен угловому коэффициенту k секущей l.
касательной к графику функции y=f(x) в точке C с абсциссой c равен угловому коэффициенту k секущей l.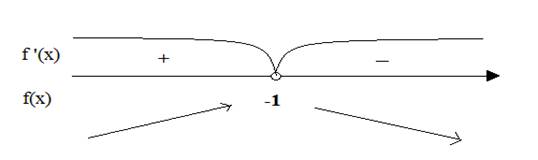
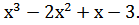
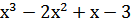 на отрезке
на отрезке