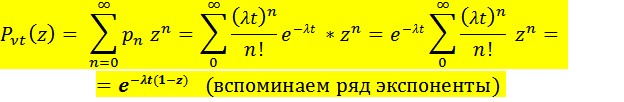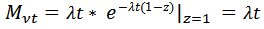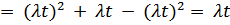Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тогда производящей функцией (пф) распределения св называетсяСодержание книги
Поиск на нашем сайте
Производящие функции Определение.Пусть Тогда производящей функцией (ПФ) распределения СВ называется
(2.16) Свойства ПФ: 1. 2. 3. 4. 5. Если 6. Если
То есть ПФ суммы случайного числа случайных величин - это ПФ числа слагаемых, а аргумент у нее не z, а ПФ каждого слагаемого (сложная функция) Следствия. Дифференцируя (2.22) нужное число раз и полагая
(2.17) (2.21)
Замечание. Если снять ограничение целочисленности, наложенное на величины
(2.25) Соотношения для математического ожидания и дисперсии остаются прежними. Рассмотрим примеры. Пример 2.4 (характеристики пуассоновского потока) На вход системы поступает пуассоновский поток заявок интенсивности Указание. Если входной поток событий обладает свойствами стационарности, ординарности и отсутствия последействия, то его называют пуассоновским потоком, так как распределение количества событий, произошедших в течение фиксированного интервала времени длины Решение.
По формуле (2.18 свойство 2 ПФ) получаем: По формуле (2.19) получаем: (цифры формул возможно сбились, проверьте!)
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 8; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.18 (0.006 с.) |

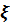 – неотрицательная целочисленная СВ, принимающая значения
– неотрицательная целочисленная СВ, принимающая значения 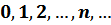 с вероятностями
с вероятностями 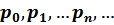 .
.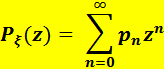
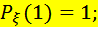
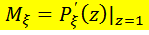
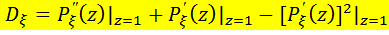
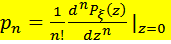
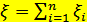 , где
, где 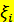 – независимые СВ, то
– независимые СВ, то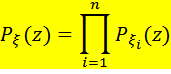 В частности, если
В частности, если 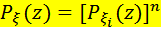
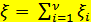 , где
, где 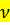 - целочисленная неотрицательная СВ,
- целочисленная неотрицательная СВ, 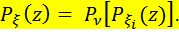
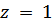 , получаем:
, получаем:
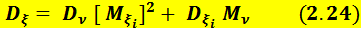
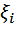 , (ξ - сумма случайного числа нецелочисленных СВ) ,то вместо (2.22) имеет место соотношение
, (ξ - сумма случайного числа нецелочисленных СВ) ,то вместо (2.22) имеет место соотношение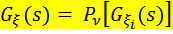
 . Обозначим
. Обозначим 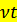 число заявок, поступающих за время
число заявок, поступающих за время 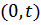 . Найти ПФ случайной величины
. Найти ПФ случайной величины 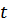 , (т.е. СВ
, (т.е. СВ  ), имеет распределение Пуассона:
), имеет распределение Пуассона: 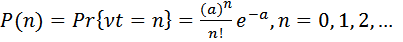 , где
, где 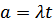 ,
,  – интенсивность потока (среднее число событий в единицу времени).
– интенсивность потока (среднее число событий в единицу времени).