
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действия над приближенными числамиСодержание книги
Поиск на нашем сайте
ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ Действительное число – это бесконечная десятичная дробь. Производить вычисления с бесконечными десятичными дробями неудобно, поэтому на практике пользуются приближенными значениями действительных чисел. Приближённые вычисления – это вычисления, в которых данные и результат (или по крайней мере только результат) являются числами, лишь приближённо представляющими истинные значения соответствующих величин. Приближённые вычисления возникают в связи с численным решением задач и обусловлены неточностями, которые присущи формулировке задачи и способам её решения. Общие правила и теорию методов приближённых вычислений принято называть численными методами. Например, для числа Приближение по недостатку и приближение по избытку называют иногда округлением числа. Пример: Имеем Погрешности Модуль разницы между точным числом x и его приближенным значением a называется абсолютной погрешностью данного приближенного числа. Da =| x - a | - погрешность приближения.
Отношение Da / a = da называется относительной погрешностью; последнюю часто выражают в процентах. 3,14 является приближенным значением числа p, погрешность его равна 0,00159..., абсолютную погрешность можно считать равной 0,0016, а относительную погрешность da равной 0,0016/3,14 = 0,00051 = 0,051%. Значащие цифры – этовсе цифры числа, начиная с 1-й слева, отличной от нуля, до последней, за правильность которой можно ручаться. Приближенные числа следует записывать, сохраняя только верные знаки.
Округление Обычно при округлении пользуются следующим правилом:если первая отбрасываемая цифра больше или равна 5, то последняя сохраняемая цифра увеличивается на единицу. При округлении сохраняются только верные знаки; лишние знаки отбрасываются по правилу округления.
Результат действий над приближёнными числами представляет собой также приближённое число. Число значащих цифр результата можно вычислить при помощи следующих правил:
1. При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных знаков, сколько их в приближённом данном с наименьшим числом десятичных знаков. 2. При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближённое данное с наименьшим числом значащих цифр. Почему же важно уметь находить приближенные значения чисел? Дело в том, что практически невозможно оперировать с бесконечными десятичными дробями и использовать их для измерения величин. На практике во многих случаях вместо точных значений берут приближения с заранее заданной точностью (погрешностью). Эта идея заложена и в калькуляторах, на дисплеях которых высвечивается конечная десятичная дробь, т.е приближение выводимого на экран числа (за редким исключением, когда выводимое число представляет собой конечную десятичную дробь, умещающуюся на экране).
|
|||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 11; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.28.66 (0.009 с.) |

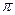 =3,141592… пользуются приближенным равенством
=3,141592… пользуются приближенным равенством 
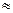 3,141 или
3,141 или 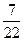 = 0,31818. Таким образом,
= 0,31818. Таким образом, 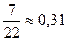 - это приближение по недостатку с точностью до 0,01;
- это приближение по недостатку с точностью до 0,01; 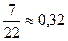 - это приближение по избытку с точностью до 0,01.
- это приближение по избытку с точностью до 0,01.


