Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перегрузка операций вызова функцийСодержание книги
Поиск на нашем сайте
Класс, в котором переопределен оператор вызова функции, называется функциональным классом. У такого класса не требуется наличие других полей и методов. Пример 1 class if_greater { Public int operator() (int a, int b) const { return a>b; } }; Объект данного функционального класса используется так, как если бы он был функцией. Пример 2 if_greater x; cout<< x(1, 5)<< endl; /* 0 */ cout << if _greater () (5, 1)<< endl; /* 1 */
Поскольку в классе определена операция вызова функции с двумя аргументами, то выражение x(1, 5) является допустимым, или это можно записать так: Пример 3 *operator()(1, 5) А во втором операторе вызова функции if_greater используется для вызова конструктор по умолчанию класса if_greater. Как и в предыдущем случае для этого объекта вызывается функция с двумя аргументами, записанными в круглые скобки. Операцию круглые скобки можно определить только как метод класса. Можно определить перегруженные операции вызова функции с разным количеством аргументов.
Перегрузка операций индексирования Операция индексирования обычно перегружается когда тип класса представляет множество значений, для которых индексирование имеет смысл. Операция индексирования должна возвращать ссылку на элемент, содержащийся во множестве. Пример 1 Пример перегрузки операции индексирования для класса Vect, предназначенного для хранения массива целых чисел и безопасной работы с ним. #include<iostream.h> #include<stdlib.h> Class Vect { public: explicit Vect (int n=10); Vect (const int a[], int n); /* инициализация массива */ ~Vect(){delete[] p;} int &operator[] (int i); void print(); private: int *p; int size; }; Vect::Vect(int n):size(n) { p=new int[size]; for (int i=0; i<size; i++) p[i]=a[i]; } /* перегрузка операции индексации */ int &Vect::operator[](int i) { if(i<0 || i>=size) { cout<<" Неверный индекс (i="<<i<<")"<<endl; cout<<"Завершение программы"<<endl; exit(0); } return p[i]; } Void Vect::Print() { for(int i=0; i<size; i++) cout<<p[i]<<" "; cout<< endl; } Int main() { int arr[10]={1,2,3,4,5,6,7,8,9,10}; Vect a(arr, 10); a Print(); cout<<a[5]<<endl; cout<<a[12]<<endl; return 0; } Результаты работы: 1 2 3 4 5 6 7 8 9 10 6 Неверный индекс (i=12) Завершение программы Перегруженная операция индексирования получает целый аргумент и проверяет, лежит ли его значение в пределах диапазона массива. Если лежит, то возвращается адрес элемента, что соответствует стандартной семантике операции индексирования. В данном примере конструктор с параметрами по умолчанию объявлен как explicit. Это сделано для того, чтобы он не являлся конструктором преобразования типа, который может быть вызван неявно. В данном случае explicit указывает на то, что этот конструктор будет вызываться явным образом.
Операцию индексирования можно определять только как метод класса.
Глава 11. Структуры данных Стек Со стеком определены только операции добавления и выборки элементов из вершины стека. При осуществлении выборки элемент исключается из стека. В стеке осуществляется принцип LIFO. Возможен также принцип FIFO. Стеки широко применяются в системном программировании при написании компиляторов и различных рекурсивных алгоритмов. Пример 1 Пример программы, которая формирует стек из пяти целых чисел, и выводит его на экран: #include <iostream> Struct Node { int d; Node *p; } Node *first(int d); void push(Node **top, int d); void pop(Node **top); Int main() { Node *top = first(1); for(int i=2; i<6; i++) push(&top, i); While(top) cout<<pop(&top)<<" "; return 0; } /* начальное формирование стека */ Node *first (int d) { Node *Pv = new Node; Pv->d=d; Pv->d=0; return Pv; } /* занесение в стек */ void push(Node **top, int d) { Node *Pv = new Node; Pv -> d = d; Pv -> p = *top; *top = Pv; } /* выборка из стека */ int pop(Node **top) { int temp = (*top) -> d; Node *Pv = *top; *top = (*top) -> p; delete Pv; return temp; } /* вывод: 5 4 3 2 1 */
Очереди Очередь – абстрактная структура данных, реализует принцип обслуживания FIFO. Это частный случай однонаправленного списка, добавление элементов в который выполняется в один конец, а выборка идет из другого конца. Таким образом, в структуре «очередь» определены две операции: добавление элементов и выборка. При выборке элемент из очереди исключается. В системном программировании очереди используются для диспетчеризации задач моделирования. Пример 1 Пример программы, реализующей линейную очередь из пяти элементов, выводя их на экран Struct Node { int d; Node *p; } Node *first(int d); void add(Node **pend, int d); int del(Node **pbeg); Int main() { Node *pbeg = first(1); Node *pend = pbeg; for(int i=2; i<6; i++) add (&pend, i); While(pbeg) cout<<del(&pbeg)<<" "; return 0; } /* начальное формирование очереди*/ Node *first(ind d)
{ Node *pv = new Node; pv -> d = 0; pv -> p = 0; return pv; } /* добавление в конец */ void add(Node **pend, int d) { Node *pv = new Node; pv -> d = d; pv -> p = 0; (*pend) -> p = pv; *pend = pv; } /* выборка */ int del(Node **pbeg) { int temp = (*pbeg) -> d; Node *pv = *pbeg; *pbeg = (*pbeg) -> p; delete pv; return temp; } Результат работы: 1 2 3 4 5
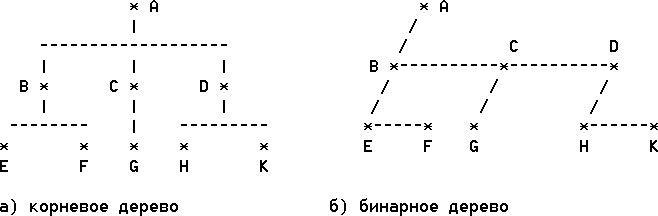
Деревья Понятие корневого дерева. В теории графов конечное корневое дерево формально определяется как непустое конечное множество узлов Т, таких что: существует один, специально выделенный узел, называемый корнем, а остальные узлы образуют попарно непересекающиеся подмножества множества узлов Т, каждое из которых является деревом. Это определение позволяет интерпретировать корневое дерево как рекурсивный объект, который содержит сам себя и определяется с помощью себя самого (т. е. дерево определяется в терминах дерева). Определение корневого дерева как определение любого рекурсивного объекта содержит базисную и рекурсивную части. Базисная часть, определяющая корень дерева, является нерекурсивным утверждением. Рекурсивная часть определения записана так, чтобы она редуцировалась (сводилась) к базе цепочкой повторных применений. В данном случае дерево с числом узлов n>1 индуктивно определяется через деревья с числом узлов меньше, чем n, пока не достигнут базисный шаг, где дерево состоит из единственного узла - корня. Рекурсивное определение корневого дерева позволяет более простым способом формализовать его структуру и алгоритмы обработки. Для неформального описания корневых деревьев часто используется генеалогическая терминология, согласно которой каждая ветвь отражает отношение потомок-предок между инцидентными ей узлами. Корень дерева – это узел, который не имеет предка. Узлы дерева, которые не имеют потомков называются листьями. Остальные узлы (не листья и не корень) называются разветвлениями. Следующий рисунок иллюстрирует классическое изображение корневого дерева средствами теории графов, где вершины и ребра графа представляют узлы и ветви дерева.
Рис. 1. Изображение корневого дерева в теории графов На этом рисунке заглавные буквы латинского алфавита обозначают узлы, а строчные- ветви корневого дерева. Конфигурация ветвей этого корневого дерева такова, что узел А является корнем, узлы В С и D- разветвлениями, а узлы E, F, G, H, и K - листьями. Следует отметить, что кроме классического изображения, принятого в теории графов, в области информационных технологий применяются альтернативные способы представления корневых деревьев. На следующем рисунке приведены 3 эквивалентных способа представления исходного корневого дерева: с помощью вложенных скобок (а), уступчатого списка (б) и десятичной системы Дьюи (в) соответственно:
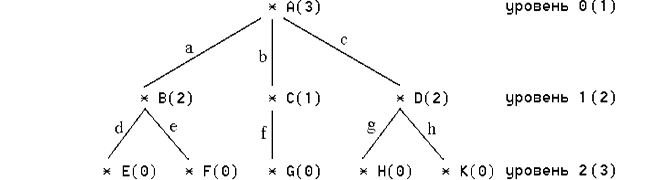
Рис. 2. Альтернативные способы представления корневого дерева Приведенные альтернативные способы представления корневых деревьев иллюстрируют возможности практического применения иерархических структур. Например, десятичная система Дьюи применяется в библиографии, а вложенные скобки - для получения полноскобочной записи при грамматическом разборе арифметических выражений. Важными метрическими характеристиками корневого дерева является степень и уровень узла. Степенью узла корневого дерева считается число поддеревьев, для которых он является корнем. Для рассмотренного примера корневого дерева: корень А имеет степень 3, степени разветвлений B и D - равны 2, а степень разветвления С равна 1. Степени остальных узлов равны 0, потому что они являются листьями, т. е. не имеют поддеревьев. Уровень узла корневого дерева определяется длиной пути, образованного чередующейся последовательностью узлов и ветвей, который соединяет его с корнем. Длина пути измеряется числом узлов в нем. Для рассмотренного примера корень А имеет уровень 1, разветвления B, C и D имеют уровень 2, а листья E, F, G, H и K - уровень 3.
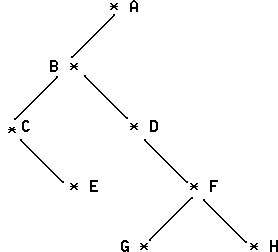
При измерении длины пути числом ветвей в нем, указанные уровни узлов надо уменьшить на 1. Обобщением понятия корневого дерева является понятие леса. Под лесом понимается упорядоченное множество непересекающихся корневых деревьев. Отражением близости этих понятий является простота преобразований дерева в лес и наоборот, леса в дерево. Исключение корня превращает дерево в лес. Наоборот, добавление одного узла превращает лес в дерево, где этот узел становится корнем. Чтобы подчеркнуть близость этих понятий, в некоторых работах для обозначения леса из N деревьев употребляют термин: дерево с N -кратным корнем. Понятие бинарного дерева. Важной разновидностью корневых деревьев является класс бинарных деревьев, где каждый узел может иметь не более 2-х потомков. В рекурсивном варианте определения бинарное дерево состоит из корня и 2-х бинарных поддеревьев: левого и правого, причем любое из них может быть пустым. Следующий рисунок иллюстрирует изображение бинарного дерева из 8-ми узлов A, B, C, D, E, F, G, H средствами теории графов.
Рис. 3. Изображение бинарного дерева в теории графов. Несмотря на иерархическую структуру, бинарные деревья не являются подмножеством множества деревьев. Например, на следующем рисунке показаны 2 различных бинарных дерева, которые эквивалентны как корневые деревья.
Рис. 4. Отличие корневых и бинарных деревьев Эти бинарные деревья различны по структуре, потому что корень первого из них имеет только левый потомок, а корень второго - только правый. Однако, как деревья они эквивалентны дереву из 2-х узлов А и В, которое и Несмотря на эти отличия бинарные деревья могут быть использованы для представления корневых деревьев. Возможность такого представления устанавливает следующее естественное соответствие между корневыми и бинарными деревьями. Левая ветвь каждого узла соединяет его с первым узлом следующего уровня, а правая - с другими узлами следующего уровня (братьями). Следующий рисунок демонстрирует естественное соответствие 3-х уровневого корневого дерева его бинарному представлению.
Рис. 5. Естественное соответствие между корневым и бинарным деревьями. Естественное соответствие между корневыми и бинарными деревьями имеет важное значение в области информационных технологий, где программирование обработки данных может быть более просто реализовано для бинарных деревьев. Классическим примером иерархической обработки данных являются алгоритмы поиска по бинарному дереву и прохождения бинарного дерева в различном порядке.
|
|||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.62.10 (0.013 с.) |


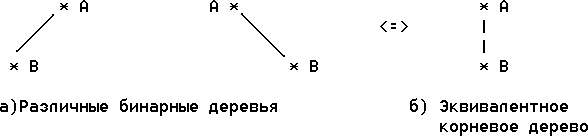 зображено на том же рисунке справа. В общем случае различие между корневым деревом и бинарным деревом состоит в том, что каждый узел корневого дерева может иметь произвольное число поддеревьев, в то время как любой узел бинарного дерева может иметь только 0, 1 или 2 поддерева и существует различие между левыми и правыми поддеревьями.
зображено на том же рисунке справа. В общем случае различие между корневым деревом и бинарным деревом состоит в том, что каждый узел корневого дерева может иметь произвольное число поддеревьев, в то время как любой узел бинарного дерева может иметь только 0, 1 или 2 поддерева и существует различие между левыми и правыми поддеревьями.