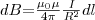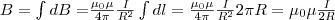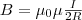Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрический заряд.Закон сохранения зарядаСодержание книги
Поиск на нашем сайте
Электрический заряд.Закон сохранения заряда Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.Электрический заряд обычно обозначается буквами q или Q.Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:Существует два рода электрических зарядов, условно названных положительными и отрицательными.Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд. Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения. Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной: q1 + q2 + q3 +... +qn = const. Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Напряженность электрического поля.Принцип суперпозиции Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля. E = F / q пр. Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд qпр, помещенный в рассматриваемую точку поля, к величине этого заряда. Понятие «пробный заряд» предполагает, что этот заряд не участвует в создании электрического поля и так мал, что не искажает его, т. е. не вызывает перераспределения в пространстве зарядов, создающих рассматриваемое поле. В системе СИ единицей напряженности служит 1 В / м, что эквивалентно 1 Н / Кл. Принцип суперпозиции. Напряжённость поля, создаваемого системой неподвижных точечных зарядов q1, q2, q3, ¼, qn, равна векторной сумме напряжённостей электрических полей, создаваемых каждым из этих зарядов в отдельности:
где ri – расстояние между зарядом qi и рассматриваемой точкой поля. Принцип суперпозиции, позволяет рассчитывать не только напряжённость поля системы точечных зарядов, но и напряженность поля в системах, где имеет место непрерывное распределение заряда. Заряд тела можно представить как сумму элементарных точечных зарядов dq. При этом, если заряд распределен с линейной плотностью t, то dq = t dl; если заряд распределен с поверхностной плотностью s, то dq = dl и dq = r dl, если заряд распределен с объёмной плотностью r. Проводники в электростатическом поле Явление разделения разноименных зарядов в проводнике, помещенном в электрическое поле, называется электростатической индукцией. При внесении в электрическое поле тела из проводника свободные заряды в нем приходят в движение. Перераспределение зарядов вызывает изменение электрического поля. Движение зарядов прекращается только тогда, когда напряженность электрического поля в проводнике становится равной нулю. Свободные заряды перестают перемещаться вдоль поверхности проводящего тела при достижении такого распределения, при котором вектор напряженности электрического поля в любой точке перпендикулярен поверхности тела. Поэтому в электрическом поле поверхность проводящего тела любой формы является эквипотенциальной поверхностью. Свойства конденсатора Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения. С точки зрения метода комплексных амплитуд конденсатор обладает комплексным импедансом
где При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью
Резонансная частота конденсатора равна
При Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:
где
Соединение конденсаторов
Рис.3
|
ЯВЛЕНие самоиндуции
При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение этого магнитного потока, в силузакона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.Это явление и называется самоиндукцией. Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока I: 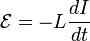 .
.
Энергия магнитного поля
Энергия магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, равна 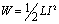 где I — сила тока в контуре. Вокруг проводника с током существует магнитное поле, которое обладает энергией.
где I — сила тока в контуре. Вокруг проводника с током существует магнитное поле, которое обладает энергией.
Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии.
В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.
Энергия магнитного поля равна собственной энергии тока.
Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.
25. Рассматривая действие магнитного поля на проводники с током и на движущиеся заряды, мы не интересовались процессами, происходящими в веществе. Свойства среды учитывались формально с помощью магнитной проницаемости m. Для того чтобы разобраться в магнитных свойствах сред и их влиянии на магнитную индукцию, необходимо рассмотреть действие магнитного поля на атомы и молекулы вещества.
Опыт показывает, что все вещества, помещенные в магнитное поле, намагничиваются. Рассмотрим причину этого явления с точки зрения строения атомов и молекул, положив в основу гипотезу Ампера, согласно которой в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах.
Для качественного объяснения магнитных явлений с достаточным приближением можно считать, что электрон движется в атоме по круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом (см. (109.2)) p m=IS n, модуль которого
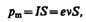
где I = en — сила тока, n — частота вращения электрона по орбите, S — площадь орбиты. Если электрон движется по часовой стрелке (рис. 187), то ток направлен против часовой стрелки и вектор р m (в соответствии с правилом правого винта) направлен перпендикулярно плоскости орбиты электрона, как указано на рисунке.
|
|
С другой стороны, движущийся по орбите электрон обладает механическим моментом импульса L e, модуль которого, согласно (19.1),
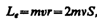
где v = 2pn, pr2 = S. Вектор L e (его направление также определяется по правилу правого винта) называется орбитальным механическим моментом электрона.
Из рис. 187 следует, что направления р m и L e, противоположны, поэтому, учитывая выражения (131.1) и (131.2), получим
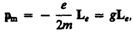
где величина
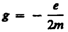
называется гиромагнитным отношением орбитальных моментов (общепринято писать со знаком «–», указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой орбиты, хотя для разных орбит значения v и r различны. Формула (131.4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит.
Экспериментальное определение гиромагнитного отношения проведено в опытах Эйнштейна и де Гааза* (1915), которые наблюдали поворот свободно подвешенного на тончайшей кварцевой нити железного стержня при его намагничении во внешнем магнитном поле (по обмотке соленоида пропускался переменный ток с частотой, равной частоте крутильных колебаний стержня). При исследовании вынужденных крутильных колебаний стержня определялось гиромагнитное отношение, которое оказалось равным –(e/m). Таким образом, знак носителей, обусловливающих молекулярные токи, совпадал со знаком заряда электрона, а гиромагнитное отношение оказалось в два раза бо2льшим, чем введенная ранее величина g (см. (131.4)). Для объяснения этого результата, имевшего большое значение для дальнейшего развития физики, было предположено, а впоследствии доказано, что кроме орбитальных моментов (см. (131.1) и (131.2)) электрон обладает собственным механическим моментом импульса L es, называемым спином. Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к целому ряду противоречий. В настоящее время установлено, что спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона L es, соответствует собственный (сотовый) магнитный момент р ms, пропорциональный L es и направленный в противоположную сторону:
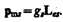
26. Парамагнетики — вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля. Парамагнетики относятся к слабомагнитным веществам, магнитная проницаемость незначительно отличается от единицы. µ≥1Атомы (молекулы или ионы) парамагнетика обладают собственными магнитными моментами, которые под действием внешних полей ориентируются по полю и тем самым создают результирующее поле, превышающее внешнее.
Диамагне́тики — вещества, намагничивающиеся против направления внешнего магнитного поля. В отсутствие внешнего магнитного поля диамагнетики немагнитны. Под действием внешнего магнитного поля каждый атом диамагнетика приобретает магнитный момент I (а каждый моль вещества — суммарный магнитный момент), пропорциональный магнитной индукции H и направленный навстречу полю. Поэтому магнитная восприимчивость χ = I/H у диамагнетиков всегда отрицательна. По абсолютной величине диамагнитная восприимчивость χ мала и слабо зависит как от напряжённости магнитного поля, так и от температуры.
Теорема Лармора: действие магнитного поля на электронную орбиту можно свести к сообщению этой орбите прецессии с угловой скоростью Ω. Прецессионное движение электронных орбит эквивалентно круговому микротоку. Так как этот микроток индуцирован внешним магжтным полем, то. согласно правилу Ленца, у атома появляется магнитный момент, направленный против внешнего поля.
Наведенные составляющие магнитных полей атомов складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле.
27. Закон Фарадея: э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
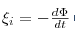
28.Магнитное поле бесконечного прямолинейного проводника с током и кругового витка с током
Правило Максвелла (правило буравчика)
Правило Максвелла позволяет определить направление вектора индукции (или линий индукции) магнитного поля тока: если ввинчивать буравчик по направлению тока в проводнике, то направление движения рукоятки укажет направление вектора индукции (линий индукции).
Примеры магнитных полей токов
Магнитное поле бесконечного прямолинейного проводника с током I:
H = (1/4p)*(2I/r)
B = (mm0/4p)*(2I/r)
где r - расстояние от проводника до точки расчета.
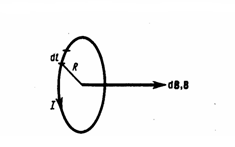
Магнитное поле на оси кругового витка радиуса R с током I на расстоянии h от центра:
H = (1/2) * (IR2) / (R2 + h2)3/2
B = (mm0/2)*(IR2) / (R2 + h2)3/2
Магнитное поле в центре кругового витка радиуса R с током I:
H = I/(2R)
B = mm0 I/(2R)
29.I уравнение Максвелла
Уравнения Максвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики.
1. Электрическое поле может быть как потенциальным (EQ), так и вихревым (EB), поэтому напряженность суммарного поля E = EQ + EB.
Так как циркуляция вектора EQ равна нулю
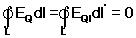
а циркуляция вектора EB определяется выражением
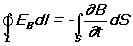
то циркуляция вектора напряженности суммарного поля
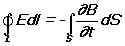
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
30. II уравнение Максвелла
2. Обобщенная теорема о циркуляции вектора H
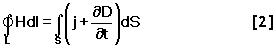
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):
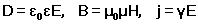
где ε0 и μ0 – соответственно электрическая и магнитная постоянная, ε и μ – соответственно диэлектрическая и магнитная проницаемость, γ – удельная проводимость вещества.
Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями.
Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных
31. Третье Максвелла уравнения выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим (магнитное поле порождается только токами):
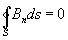 , (1, в)
, (1, в)
то есть поток вектора магнитной индукции через произвольную замкнутую поверхность S равен нулю.
Четвёртое Максвелла уравнения (обычно называемое Гаусса теоремой) представляет собой обобщение закона взаимодействия неподвижных электрических зарядов — Кулона закона:
 , (1, г)
, (1, г)
поверхность то есть поток вектора электрической индукции через произвольную замкнутую S определяется электрическим зарядом, находящимся внутри этой поверхности (в объёме V, ограниченном данной поверхностью).
Эффект Холла
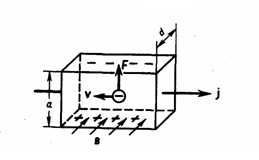
Эффект Холла — это возникновение в металле (или полупроводнике) с током плотностью j, который помещен в магнитное поле В, электрического поля в направлении, перпендикулярном В и j.
Металлическую пластинку с током плотностью j поместим в магнитное поле В, перпендикулярное j (рис. 1). При заданном направлении j скорость носителей тока в металле (в данном случае - электронов) направлена справа налево. На электроны действует сила Лоренца, направленная в данном случае вверх. Значит, у верхнего края пластинки создается повышенная концентрация электронов (отрицательно зарядится), а у нижнего — их недостаток (положительно зарядится). В результате этого между краями пластинки появится дополнительное поперечное электрическое поле, которое направленно снизу вверх. Когда напряженность ЕB данного поперечного поля достигнет величины, при которой его действие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Тогда
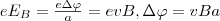
где Δφ — поперечная (холловская) разность потенциалов, а — ширина пластинки.
Учитывая, что сила тока I=jS=nevS (n — концентрация электронов, S — площадь поперечного сечения пластинки толщиной d, v — средняя скорость упорядоченного движения электронов), найдем
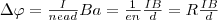 (1)
(1)
т. е. холловская поперечная разность потенциалов прямо пропорциональна магнитной индукции В, силе тока I и обратно пропорциональна толщине пластинки d. В формуле (1) R=1/(en) — постоянная Холла, которая зависит от вещества. Измеряя значение постоянной Холла можно: 1) найти концентрацию носителей тока в проводнике (при известных зарядах носителей и характере проводимости); 2) делать выводы о природе проводимости полупроводников, поскольку знаки постоянной Холла и знаки заряда е носителей тока совпадают. По этой причине эффект Холла наиболее эффективный метод изучения энергетического спектра носителей тока в металлах и полупроводниках. Он используется и для умножения постоянных токов в аналоговых вычислительных машинах, в измерительной технике (датчики Холла) и т. д.
Механические колебания.
Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат  около положения равновесия, принятого за начало координат. Тогда зависимость координаты
около положения равновесия, принятого за начало координат. Тогда зависимость координаты  от времени задаётся уравнением, аналогичным уравнению
от времени задаётся уравнением, аналогичным уравнению 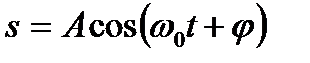 , где
, где  . Согласно выражениям
. Согласно выражениям  и
и 
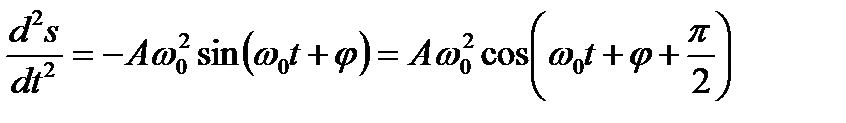 , скорость
, скорость  и ускорение
и ускорение 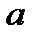 колеблющейся точки соответственно равны указанным выражениям (первая производная – скорость, вторая – ускорение). Сила
колеблющейся точки соответственно равны указанным выражениям (первая производная – скорость, вторая – ускорение). Сила 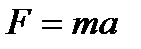 , действующая на колеблющуюся материальную точку массой
, действующая на колеблющуюся материальную точку массой 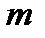 , с учётом вышеуказанных выражений, равна
, с учётом вышеуказанных выражений, равна 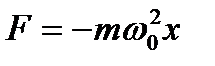 . Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена к противоположную сторону (к положению равновесия).
. Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена к противоположную сторону (к положению равновесия).
БИЕНИЕ
колебания с периодически меняющейся амплитудой, возникающие в результате наложения двух гармонических колебаний (См. Гармонические колебания) с несколько различными, но близкими частотами. Б. возникают вследствие того, что разность фаз между двумя колебаниями с различными частотами всё время изменяется так, что оба колебания оказываются в какой-то момент времени в фазе, через некоторое время — в противофазе, затем снова в фазе и т.д. Если А1 и А2 — амплитуды двух накладывающихся колебаний, то при одинаковых фазах колебаний амплитуда результирующего колебания достигает наибольшего значения A1 + A2, а когда фазы колебаний противоположны, амплитуда результирующего колебания падает до наименьшего значения A1 — A2. В простейшем случае, когда амплитуды обоих колебаний равны, их сумма достигает значения 2А при одинаковых фазах колебаний и падает до нуля, когда они противоположны по фазе (рис.). Результат наложения колебания можно записать в виде:
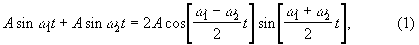
где ω1 и ω2 — соответственно угловые частоты двух накладывающихся гармонических колебаний (начальные фазы обоих колебаний полагаются равными нулю, т.к. они не играют роли в образовании Б.; играет роль только разность фаз между обоими колебаниями, которая всё время меняется от 0 до 2π).
Если ω1 и ω2 мало различаются, то в выражении (1) величину
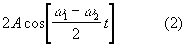
можно рассматривать как медленно меняющуюся амплитуду колебания
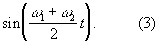
По физической природе
§ Механические (звук, вибрация)
§ Электромагнитные (свет, радиоволны, тепловые)
§ Смешанного типа — комбинации вышеперечисленных
Принцип Гюйгенса-Френеля
Принцип Гюйгенса — Френеля формулируется следующим образом: Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн. Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых.
49.Дифракция Френеля.
Дифракция Френеля представляет собой наблюдающуюся на небольшом расстоянии от препятствия дифракционную картину, при таких условиях, когда интерференционная картина изменяется благодаря границам экрана.
Приведём пример такой дифракции на круглом отверстии.
Через отверстие на одном экране проходит свет, и расходится вследствие дифракции, в то время как на другом экране фиксируется изображение. Из-за этого затемнённая область становится частично освещённой. А в области, которая должна была быть освещённой, интенсивность освещения колеблется, причём в виде концентрических колец.
Зная, что каждая точка на границе отверстия излучает сферическую волну, можем рассчитать дифракцию Френеля, учитывая, что она зависит от расстояния между экранами и от расположения источников света. При этом следует принять во внимание кривизну волнового фронта.
Существует такое выражение, как приближение Френеля, для которого существует условие применимости, хоть и довольно слабое:
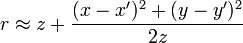 , усл.:
, усл.: 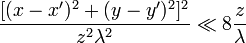 .
.
При верном определении фаз интерферирующих волн, можем записать формулу электрического поля для дифракции Френеля в точке (x,y,z):
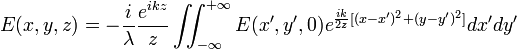 ;
;
Дифракция Френеля: 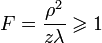 .
.
50.Дифракция Фраунгофера.
При дифракции Фраунгофера дифракционная картина наблюдается на значительном расстоянии от преграды либо отверстия.
При теоретическом рассмотрении явления берём такое расстояние, чтобы можно было пренебречь членами порядка 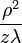 для разности фаз, где z — расстояние от отверстия или преграды до плоскости наблюдения, λ — длина волны излучения, а ρ — координата рассматриваемой точки в плоскости наблюдения полярной системы координат.
для разности фаз, где z — расстояние от отверстия или преграды до плоскости наблюдения, λ — длина волны излучения, а ρ — координата рассматриваемой точки в плоскости наблюдения полярной системы координат.
То есть, дифракция Фраунгофера наблюдается при 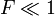 зон Френеля, причём волны, приходящие в точку, практически плоские. Поэтому можно сказать, что при дифракции Фраунгофера изображение объекта не искажается и меняет только размер и положение в пространстве.
зон Френеля, причём волны, приходящие в точку, практически плоские. Поэтому можно сказать, что при дифракции Фраунгофера изображение объекта не искажается и меняет только размер и положение в пространстве.
Запишем формулу дифракции: 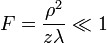 .
.
Интеграл дифракции Фраунгофера (в скалярном виде):
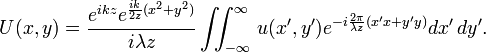
Практическое значение дифракционных явлений Фраунгофера заключается в действии по их принципу спектральных приборов, например таких, как дифракционные решётки, которые представляют собой часто расположенных на некоторой поверхности штрихов.
Электрический заряд.Закон сохранения заряда
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.Электрический заряд обычно обозначается буквами q или Q.Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:Существует два рода электрических зарядов, условно названных положительными и отрицательными.Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда.
В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной: q1 + q2 + q3 +... +qn = const.
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.
|
| Поделиться: |

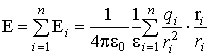
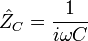 ,
,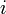 — мнимая единица,
— мнимая единица, 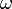 — частота[2] протекающего синусоидального тока,
— частота[2] протекающего синусоидального тока, 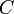 — ёмкость конденсатора. Отсюда также следует, что реактивное сопротивление конденсатора равно:
— ёмкость конденсатора. Отсюда также следует, что реактивное сопротивление конденсатора равно: 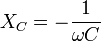 . Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).
. Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).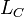 и сопротивлением потерь
и сопротивлением потерь 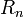 .
.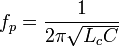
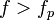 конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах
конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах 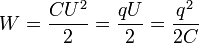
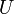 — напряжение (разность потенциалов), до которого заряжен конденсатор.
— напряжение (разность потенциалов), до которого заряжен конденсатор.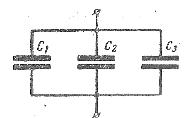 Рис. 1. Схема параллельного соединения конденсаторов
Общая емкость равнозначного (эквивалентного) конденсатора:
C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3,
т. е. при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов.
Последовательное соединение конденсаторов
При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны: Q1 = Q2 = Q3 = Q
Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды.
Рис. 1. Схема параллельного соединения конденсаторов
Общая емкость равнозначного (эквивалентного) конденсатора:
C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3,
т. е. при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов.
Последовательное соединение конденсаторов
При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны: Q1 = Q2 = Q3 = Q
Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды.
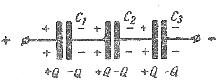 Схема последовательного соединения конденсаторов
Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3
Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.
Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.
Схема последовательного соединения конденсаторов
Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3
Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.
Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.
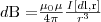 (1)
(1) 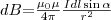 (2)
(2) 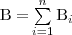 (3)
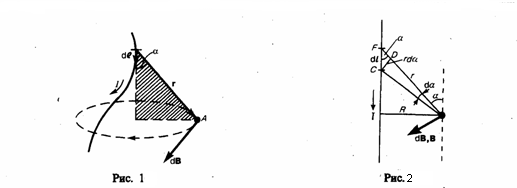
(3) 
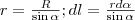
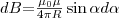 (4)
(4) 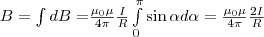
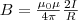 (5)
(5)