
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерпретация данных акустического каротажаСодержание книги
Поиск на нашем сайте
Характеристики упругости горных пород
Значения наиболее изученных характеристик упругости горных пород изменяются соответственно в пределах: v Р = 200 ÷ 8800 м/с, Е = (0,01 ÷ 2,35)∙1011 Па. По убыванию предельных значений скорости распространения упругих волн и модуля Юнга группы пород располагаются в ряд: магматические (v Р = 2520 ÷ 8770 м/с, Е= (0,1÷2,3)∙1011 Па), метаморфические (v Р =1450 ÷ 7600 м/с, Е =(0,05 ÷ 1,91)∙1011 Па), осадочные (v Р =300 ÷ 7600 м/с, Е =(0,01 ÷ 1,75)∙1011 Па). Наименее упругими являются осадочные породы. Особенно малые значения v Р или Е у них имеют высокопористые, малоплотные разности, а высокие значения этих величин характерны для низкопористых относительно плотных образцов песчаников, известняков, доломитов и других осадочных пород. Значений модуля сдвига G получено, относительно мало, и они нередко примерно вдвое меньше, чем соответствующие значения модулей Юнга. Значения коэффициента Пуассона ν пород изменяясь от 0,04 до 0,6, чаще всего находятся в пределах 0,18 ÷ 0,35. У преимущественно кварцевых пород, таких, как некоторые разности алевролитов, песчаников ν = 0,054 ÷ 0,15. Обнаружены также разности осадочных пород (глин, алевролитов, песчаников, каменной соли, угля), которым соответствуют ν = 0,4 ÷ 0,6. Такие высокие значения, по-видимому, относятся к очень низкопористым образцам, содержащим, много минералов с высокими значениями ν. В сцементированных осадочных породах (глинах, песчаниках, карбонатах) v Р изменяется от 2500 до 7300 м/с, v S − от 1500 до4200 м/с. В рыхлых несцементированныхпородах v Р снижается до 900÷2500 м/с, а в неуплотненных четвертичных осадках вблизи дневной поверхности до 200÷1500 м/с. Скорость поперечной волны в таких породах составляет несколько сотен метров в 1 с и ее не всегда удается зарегистрировать при АК.
Решение геологических задач
Значения скоростей распространения, амплитуд и эффективного затухания волн, регистрируемых при АК, определяются большим количеством факторов: литологическим составом пород, структурой порового пространства, коэффициентом пористости и проницаемости, характером насыщенности, наличием обсадной колонны, полнотой заполнения затрубного пространства цементом и степенью его сцепления с колонной и горными породами, свойствами жидкости в стволе скважины. Выявленные закономерности подвержены влиянию температуры и давления на глубине залегания исследуемых сред, интенсивности и частоты применяемых колебаний. При первичной интерпретации данных АК, путем прослеживания первой положительной фазы колебаний на ФКД по каждому измерительному зонду, получают кривые времени первого вступления T 1 и Т2 . Вычисляются интервальное время ΔТ распространения и к оэффициент затухания a амплитуды упругих волн на базе зонда S
Рис.14. Схема распространения упругих волн в скважине и их параметры.
Интерпретация данных акустического каротажа Акустические методы исследования разрезов скважин основаны на определении упругих свойств горных пород по данным наблюдений за распространением в них упругих волн. Многолетний опыт применения акустического каротажа показал его высокую информативность при решении широкого спектра задач, возникающих при исследовании нефтяных и газовых скважин на этапе разведки и разработки месторождений. В процессе развития каротажа определились четыре наиболее перспективных направления применения его данных: · Литологическое расчленение разрезов скважин, оценка пористости, трещиноватости и кавернозности пород; · Оценка характера насыщения пластов, определение зон вторичной трещиноватости при контроле за разработкой и интенсификацией добычи; · оценка технического состояния обсаженных скважин; · построение геоакустических моделей сред с целью интерпретации материалов сейсмической разведки. Эффективность решения большинства перечисленных выше задач определяется, в основном, качеством решения трех принципиальных проблем акустического каротажа: · выделение и идентификация информативных типов акустических волн в условиях их интерференции с регулярными волнами-помехами; · достоверное измерение кинематических и динамических параметров волн, в том числе в интервалах высокого затухания; · установление достоверных зависимостей между параметрами акустических волн и фильтрационно-емкостными свойствами коллекторов, их флюидонасыщенностью, свойствами и характеристиками элементов конструкции скважин и разработка на основе этих зависимостей эффективных алгоритмов решения обратных задач. Следует отметить, что две первые проблемы могут быть решены путем совершенствования аппаратуры, технологии измерений и интерпретации данных каротажа; решение третьей – это область теоретических и экспериментальных петрофизических исследований, а также математического и физического моделирования объектов исследования. Прогресс, достигнутый в последние годы в области акустических исследований скважин, обусловлен использованием цифровой аппаратуры и развитием современных способов обработки волновых полей.
Упругие волны: определения и условия распространения Если в ограниченной области среды в течение некоторого короткого времени действует внешняя возбуждающая сила, то в результате в этой области среды возникает деформация, и будет наблюдаться перемещение частиц среды во всех направлениях от точки приложения возбуждающей силы, т. е. возникнет периодический процесс последовательного распространения деформации, который называется упругой волной. Этот процесс сопровождающиеся переносом энергии упругой деформации без переноса вещества. Деформацией называют перемещение отдельных частиц среды относительно друг друга под действием внешних сил. Обратимые деформации, исчезающие после снятия нагрузки, называют упругими, в противном случае – неупругими. Среду, в которой нет перехода механической энергии колебаний в тепловую, называют идеально упругой. Горные породы в естественном залегании практически являются (по крайней мере, для тех напряжений, которые возникают при акустическом каротаже) упругими телами. Упругие деформации можно разделить на деформации растяжения (сжатия), вызывающие изменение объема частиц (без изменения формы), и деформации сдвига, обусловливающие изменение формы (без изменения объема). Поверхность, отделяющая в данный момент времени область среды, в которой волна уже вызвала колебания частиц, от области, где возмущения еще не наблюдаются, называется передним фронтом (или фронтом) волны. Линию, вдоль которой происходит распространение волны, в каждой своей точке образующую прямой угол с фронтом волны в соответствующий момент времени, называют лучом волны. В однородной изотропной безграничной твёрдой среде, обладающей упругостью объёма и формы, распространяются упругие волны двух типов: продольные Р и сдвиговые или поперечные S. По форме фронта волны они могут быть плоскими, сферическими и цилиндрическими. Форма фронта определяется отношением размеров источника излучения к длине волны l. Если размеры (линейные или радиальные) излучающей поверхности превышают длину волны во много раз, то волна плоская. Вдоль пути распространения поверхность фронта плоской волны не изменяется; амплитуды колебаний и энергия волны в идеально упругой среде не изменяются; геометрический коэффициент расхождения равен нулю. Фронт цилиндрической волны, сформированной источником, протяжённость которого много больше его диаметра, увеличивается с расстоянием пропорционально удалению r от источника; убывание амплитуд пропорционально r -1/2, убывание энергии – квадрату амплитуды. Размеры сферического излучателя много меньше длины волны; амплитуды волны убывают с удалением от источника пропорционально r –1, энергия – r –2. В приборах акустического каротажа размеры излучателей, по отношению к длине упругой волны в жидкости, находятся где-то в середине между цилиндрическим и сферическим. Принимается, что коэффициент убывания энергии находится в пределах от 3/2 до 2. Тип волны (продольная, поперечная и т.д.) определяется двумя характеристиками: траекторией колебаний частиц среды и скоростью v её распространения в данной среде, затронутых волновым процессом. Другие характеристики волны – частота f и частотный спектр колебаний, амплитуды А, энергия Е – весьма важны для её описания, особенно на фоне колебаний других волн, но не определяют физической сути волны. В жидкостях и твердых телах упругие колебания распространяются в виде продольной волны. Продольная волна несет с собой только деформации объема. Распространение продольной волны представляет собой процесс перемещения зон растяжения и сжатия по направлению распространения волны, при этом частицы среды совершают колебания около своего первоначального положения. В продольной волне направления колебаний частиц параллельны направлению её распространения. Кроме того, в твердом теле образуется поперечная волна, которая связана с деформациями формы. Процесс распространения поперечной волны сводится к скольжению слоев среды относительно друг друга, при этом частицы среды совершают колебания около своего первоначального положения в направлении, перпендикулярном направлению распространения волны. Жидкости не имеют формы, следовательно, невозможна ее деформация, т. е. поперечные волны, могут существовать только в твердых телах. В однородной изотропной безграничной среде все направления сдвиговых колебаний равноправны. Однако, если имеется ограничивающая безграничную среду поверхность или поверхность разрыва в среде, под углом к которым распространяется поперечная волна (применительно к исследованиям скважин это будут стенка скважины, границы литологических пластов, крупные трещины или совокупности трещин), то возникает вопрос о направлении колебаний частиц среды по отношению к этим поверхностям. Волну, в которой направление колебаний частиц перпендикулярно ограничивающей поверхности, называют вертикально поляризованной или SV-волной. Если колебания происходят в плоскости, параллельной границе раздела, то это горизонтально поляризованная волна SН. Поперечная SV-волна образуется при преломлении продольной (Р) волны на упомянутых поверхностях. Волну SН трудно возбудить таким образом, так как в падающей Р волне отсутствует компонента, перпендикулярная плоскости падения. В дальнейшем, если отсутствует специальная оговорка, будет идти речь о поперечной волне SV (или просто S) с вертикальной поляризацией Одной из важных характеристик кинематики упругой волны является скорость ее распространения. Эта скорость зависит от упругих свойств среды и типа волны. Для характеристики свойств идеально упругих однородных и изотропных сред обычно используется одна из следующих пар констант: модуль Юнга Е (модуль продольной упругости) и коэффициент Пуассона ν (коэффициент поперечного сжатия); модуль сдвига G (коэффициент Ламе) и модуль всестороннего (объемного) сжатия (растяжения) К. Если относительную объемную деформацию тела
то модуль Юнга будет коэффициентом пропорциональности между растягивающим (сжимающим) напряжением р X (или р Y и р Z) и соответствующей ему относительной линейной деформацией е X (или е Y и е Z):
Это выражение часто называют уравнением или законом Гука для линейных деформаций. Коэффициент Пуассона − отношение относительных линейных деформаций тела в направлении, поперечном действию напряжения, к относительной линейной деформации в продольном направлении: Для случая всестороннего равномерного сжатия твердого тела закон Гука принимает вид:
где Модуль сдвига Для идеально упругих изотропных горных пород скорости распространения продольных и поперечных волн можно выразить следующим образом:
где s п – плотность породы. Для идеально упругих сред Продольную и поперечную волны, распространяющиеся в изотропных безграничных средах без поверхностей раздела или при их присутствии, называют объёмными волнами. В неидеально упругих средах, к которым принадлежат даже самые плотные горные породы с малой пористостью, распространение упругих волн сопровождается поглощением их энергии вследствие проявлений вязкости (неидеальная упругость) и неидеального теплообмена. Распространение объёмных Р и S волн происходит с дисперсией фазовых скоростей. На частотах акустического каротажа значения дисперсии не превышают нескольких первых процентов и обычно ими пренебрегают вследствие их малости и невозможности определения. Величину, обратную скорости распространения упругой волны в породе, принято называть интервальным временем ∆T. Наряду со скоростью распространения важной характеристикой волнового процесса является длина волны λ (в м), представляющая собой пространственный период колебаний. Длина волны связана со скоростью v и частотой f колебаний λ= v ⁄ f. Длина волны определяет условия ее распространения: например, продольные и поперечные волны распространяются в телах, геометрические размеры которых, по крайней мере, в 3 раза превышают длину волны; в стержнях и трубах, диаметр которых меньше λ, продольные колебания распространяются в виде волны растяжения и т. п. Распространение упругих волн в горных породах сопровождается постепенным уменьшением их энергии вследствие физических процессов поглощения, рассеяния и геометрического расхождения. Поглощение вызвано эффектами внутреннего трения, теплопроводности и молекулярного поглощения среды и приводит к необратимому превращению энергии волны в другие виды энергии. При рассеянии энергия переходит в энергию волн других типов, возникающих под действием падающей волны. При АК регистрируют не энергию волн, а их амплитуды А,связанные с энергией выражением Е=2π2 s 2 f 2А2 (Дж/м3). Уменьшение амплитуды колебаний с увеличением расстояния от источника возбуждения до точки наблюдения для случая плоского фронта распространения упругой волны происходит по экспоненциальному закону
где A0, А – соответственно амплитуды колебаний вблизи источника возбуждения и точки наблюдения, ℓ – расстояние, пройденное волной, a – коэффициент поглощения (затухания) упругих волн. Коэффициент поглощения упругих волн a является показателем потери энергии волн в горных породах вследствие указанных выше физических процессов.
Наиболее распространенная единица измерения коэффициента поглощения – децибел на метр (дБ/м). В горных породах на частотах АК эффективное затухание продольной и поперечной волн вызвано в большей степени рассеянием, чем поглощением. Поэтому амплитуды и эффективное затухание используют для выделения в породах различных неоднородностей, в первую очередь трещин, каверн, границ пластов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 610; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.245.158 (0.008 с.) |

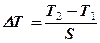 (мкс/м),
(мкс/м), 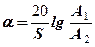 (дБ/м).
(дБ/м).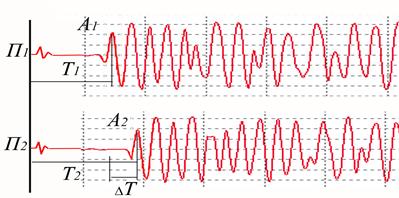
 представить в виде суммы относительных линейных деформаций по осям координат
представить в виде суммы относительных линейных деформаций по осям координат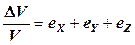 ,
,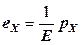 .
.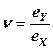 .
.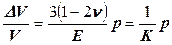 ,
,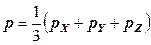 − среднее нормальное напряжение,
− среднее нормальное напряжение, 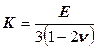 − модуль всестороннего сжатия (растяжения), определяющий пропорциональность между относительным объемным сжатием (растяжением)
− модуль всестороннего сжатия (растяжения), определяющий пропорциональность между относительным объемным сжатием (растяжением) 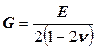 определяет пропорциональность между сдвиговым (касательным) напряжением и сдвиговой деформацией.
определяет пропорциональность между сдвиговым (касательным) напряжением и сдвиговой деформацией.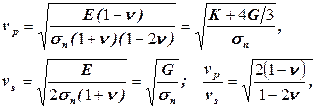
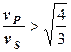 . Фазовые и групповые скорости продольной и поперечной волн в таких средах не зависят от частоты и амплитуд колебаний и формы фронта волны; дисперсия скоростей отсутствует.
. Фазовые и групповые скорости продольной и поперечной волн в таких средах не зависят от частоты и амплитуд колебаний и формы фронта волны; дисперсия скоростей отсутствует.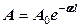 ,
,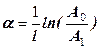 .
. 


