Тема: Динамические параметры потока в трубопроводе.

 

Цель работы: изучить существующие параметры, характеризующие динамическиепараметры потока в трубопроводе. Научиться определять значение этих параметров.

 

Общие сведения.

 

Жидкие и газообразные вещества обладают свойством изменения своей формы. Соответственно, воздействуя на них в замкнутых системах можно добиться перемещения потока вещества внутри системы. В зависимости от того как на них воздействовать возникают различные результаты перемещения вещества. Возникают медленные течения или быстрые - ламинарные (устоявшиеся) или турбулентные (с перемешиванием слоев). Каждый вид течения или режим обладает рядом свойств или параметров, которые математически характеризуют состояние потока. По ним можно смоделировать и понять, что происходит внутри замкнутой и закрытой системы. Поняв это, можно воздействовать на поток с целью его управления и получения необходимого режима перемещения.

 

В гидравлике существует ряд параметров характеризующих состояние потока.

Расход жидкости.

Расход воды — объём воды, протекающей через поперечное сечение трубопровода за

 

единицу времени. Измеряется в расходных единицах (м³/с). В промышленности расход воды (жидкости) измеряется расходомерами. Определяется

 

 

Q=W/t,

где Q - расход жидкости, м³/с,

 

W – объем перемещенной жидкости, за единицу времени, м³,

t – время, в течении которого был перемещен объем жидкости, с.

 

На поток жидкости в системе действует сила, заставляющая поток постоянно перемещаться, при этом его перемещение, расход во всех точках системы одинаков, это подтверждает уравнение неразрывности потока:

 

S 1 *V 1 =S 2 *V 2 =…=S i *V i =const,

где 1, 2, i – номер сечения в трубопроводе,

 

S1, S2, Si – значение площади сечений 1, 2, i, м²,

V1, V2, Vi – значение скорости потока в сечениях 1, 2, i, м²/с.

 

Произведение площади сечения и скорости потока в этом сечении, во всех сечениях потока одинаковы. Так как произведение скорости потока и площади его сечения является раходом жидкости, то соответственно расход жидкости в замкнутом трубопроводе во всех точках одинаковый.

 

Q= S*V,

где Q - расход жидкости, м³/с,

 

S – площадь сечения потока, м²,

V –скорость потока, м²/с.

 

Режимы течения жидкости.

 

Возможны два режима течения жидкости в трубах: ламинарный и турбулентный. Ламинарный режим течения, или просто ламинарное течение - это слоистое течение без

 

перемешивания жидкости и без пульсации (колебаний) скоростей и давлений.

 

В частном случае - при ламинарном течении жидкости в прямой трубе постоянного проходного сечения - все линии тока (траектории частиц) параллельны оси трубы и, следовательно, прямолинейны. В общем же случае ламинарного течения - форма линий тока определяется конфигурацией стенок, ограничивающих поток.

 

Турбулентное течение - это течение, сопровождающееся перемешиванием жидкости

 

и пульсациями скоростей и давлений. При турбулентном течении движение отдельных частиц является беспорядочным, а их траектории имеют разнообразный вид. Наряду с основным продольным движением частицы жидкости имеют и поперечные перемещения, что

 

и вызывает перемешивание жидкости.

По определенному соотношению величин - скорости течения потока V, диаметром трубы d,

 

и кинематической вязкостью текущей жидкостиv v, можно определить характеризующий режим течения жидкости в трубопроводе – число Рейнольдса (Re):

 

Re=V*d/ v,

 

Критическое значение этого параметра составляет Re кр =2320. То есть если расчетное значение числа Рейнольдса по имеющим условиям менее 2320, то режим движения жидкости ламинарный, если более 2320 то соответственно турбулентный. Соответственно критичным для перемещающегося потока жидкости с вязкостью v, в трубопроводе с диаметром d, является скорость. Чем скорость выше, тем более себя будет проявлять турбулентность.

 

Зону турбулентного движения принято разделять на несколько зон:

- переходная зона - не вполне развитый турбулентный поток (число Рейнольдса

 

находящемся в диапазоне от 2300 до 4000),

- турбулентный поток (число Рейнольдса от 4000 до 10000),

- далее зоны с значительными значениями числа Рейнольдса, например диапазоны

 

, более , и т. д.

 

Каждая зона характеризуется своей специфичностью, существованием ряда эмпирических зависимостей, влияния определенных параметров на значение и зависимость коэффициентов системы и т. д.

Гидравлические системы с такими значительными значениями числа Рейнольдса существую т в производстве и промышленности. Их контроль моделирование позволяет управлять режимами перемещения потоков веществ.

 

Физический смысл числа Рейнольдса заключается в том, что это число есть величина пропорциональная отношению сил инерции к силам трения, вызываемым вязкостью. Имеются в виду силы, действующие в потоке жидкости на те или иные ее объемы.

 

Число Рейнольдса имеет большое значение в гидравлике, так как является основным критерием гидродинамического подобия напорных потоков, т.е. подобия потоков несжимаемой жидкости, которое складывается из геометрического, кинематического и динамического подобия.

 

Напор потока.

 

Для произвольно выбранного сечения элементарной струйки идеальной жидкости уравнение Д. Бернулли имеет вид

H = z +	p	+	V 2	= const,
	γ		2 g

 

где z – геометрическая высота (вертикальная отметка положения) центра сечения струйки; p – давление в данном сечении струйки; V – скорость течения струйки в данном сечении; –удельный вес жидкости; g – ускорение свободного падения.

 

Сумма этих трёх слагаемых составляет полный напор струйки. Все три слагаемых могут изменяться, но их сумма (полный напор H) остаётся неизменной. Это справедливо только для идеальной среды (жидкости или газа) вследствие полного отсутствия у неё вязкости.

 

Все реальные жидкости обладают вязкостью, и поэтому вышеприведённое уравнение Бернулли для них требует корректировки.

 

Для двух произвольно выбранных сечений 1 и 2 потока реальной жидкости уравнение Бернулли в свёрнутом виде с учётом сил вязкости имеет вид:

 

H ₁= H ₂+ h _пот,

 

где Н ₁ и Η ₂ – полные напоры потока жидкости в сечениях 1 и 2; h _пот – суммарные потери напора между сечениями 1 и 2. Эти потери представляют собой необратимые затраты энергии (напора) потока жидкости на перемешивание жидкости, водовороты, завихрения и на преодоление сил вязкости (сил трения). Поэтому всегда напор потока реальной жидкости или газа по ходу течения уменьшается.

 

В развёрнутой форме уравнение Бернулли для вязкой жидкости имеет вид:

 

z +

p

+ α

V 1^2 ср

= z

+

p

2

+ α

V 2^2 cp

+ h

,

1

γ

^1 2 g

γ

2 g

1

2

2

ПОТ

где z ₁ и z ₂ – геометрические высоты центров сечений 1 и 2, м; p ₁ и p ₂ – давления в сечениях 1 и 2, Па; V 1ср и V 2ср – средние скорости в сечениях 1 и 2, м/с; ά 1 и ά 2 – коэффициенты Кориолиса;

 

g – удельный вес жидкости, Н/м³; g = 9,81 м/с² – ускорение свободного падения; h _пот – потери напора между сечениями 1 и 2, м.

Скоростной напор потока реальной жидкости, вычисленный по средней скорости, отличается от реального скоростного напора потока. Для компенсации этого различия вводят поправочный коэффициент кинетической энергии (коэффициент Кориолиса) ά, который вычисляют по формуле

∫ V ³ ds _.

^{α = S} _{V cp} 3 _s

 

Коэффициент Кориолиса представляет собой отношение действительной кинетической энергии потока жидкости к кинетической энергии потока, вычисленной по средней скорости потока. Величина коэффициента Кориолиса зависит от режима течения жидкости: при ламинарном режиме он равен двум, а при развитом турбулентном режиме он изменяется в пределах 1,05–1,02 и для упрощения расчётов его принимают равным единице.

 

С энергетической точки зрения, составляющие полного напора в уравнениях Бернулли представляют собой:

z – удельную, т.е. отнесённую к единице весового расхода жидкости, потенциальнуюэнергию положения. Её называют геометрическим (нивелирным) напором;

 

p / γ – удельную, т.е. отнесенную к единице весового расхода жидкости, энергию давления.Её называют пьезометрическим напором;

 

V ²/(2g) – удельную, т.е. отнесенную к единице весового расхода жидкости, кинетическуюэнергию. Её называют скоростным напором.

 

Геометрический и пьезометрический напоры в сумме составляют гидростатический напор,

т.е.

H _CT = z + p / γ.

 

Значение напора в точке трубопровода, можно определив, замерив ее величину. С помощью приборов измерения давления или пьезометра и т. д. Пьезометр наглядно покажет величину напора в замеряемой точке. Знание величины напора в заданных точках позволяет быстро определять величины потерь напора потока и контролировать их.

 

Если нет возможности замерить приборами и определить значение напора в заданной точке, то величину напора можно определить путем направления потока вертикально. Высота струи и даст значение напора в точке.

 

Подытожив вышесказанное можно выделить:

1. Расход жидкости во всех точках одинаков.

2. Сумма всех расходов жидкости в системе, равна значению расхода в начальной точке.

 

3. Величина напора жидкости уменьшается с отдалением от начальной точки системы – точки запитывания, в связи с увеличением потерь напора.

 

4. Расход жидкости, в системе с гидромашиной, в начальной точке равен значению подачи жидкости этого устройства.

 

5. Напор жидкости, в системе с гидромашиной, в начальной точке равен значению создаваемого напора жидкости этого устройства.

 

6. Значения величин в пунктах 5 и 6 являются паспортными данными гидромашины.

 

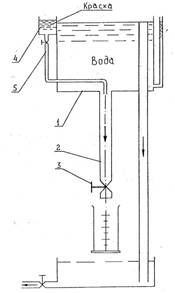
Для изучения и наглядности определения режимов потоков жидкостей используют следующую установку.

 

Рис. 3.1. Схема установки изучения режимов движения жидкости в трубопроводе.

1- емкость с жидкостью, 2. – стеклянная труба, 3- кран, 4 – сосуд с водным раствором краски,

5 – трубка для введения потока краски внутрь потока жидкости в стеклянной трубки.

 

Регулируя скорость потока краном 3, мы увеличиваем скорость истечения жидкости из емкости 1. Увеличивая степень открытия крана 3, мы увеличиваем степень турбулентности потока. Чернила подаваемые в стеклянную трубку 2, при ламинарном течении не перемешиваются с основной жидкостью. При турбулентном потоке, нет устоявшегося режима истечения и слои жидкости бурно перемешиваются, соответственно вода вся будет окрашена чернилами. Регулируя проходимость воды можно добиться переходных режимов и рассчитать критическое значение чисел Рейнольдса для переходных режимов.