
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа для заочного отделения.Содержание книги
Поиск на нашем сайте
Вариант № 2 ЗАДАНИЕ 1. 1. Три конденсатора можно соединить последовательно, параллельно и по схемам смешанного соединения. Сколько схем соединения можно построить из трех конденсаторов одинаковой емкости С и какая из них имеет наименьшую эквивалентную емкость? 2. Проводники характеризуются величинами сопротивления R и удельного сопротивления ρ. В чем состоят физическое свойство и различие этих величин? 3. В момент включения электроплитки яркость уже горящей электролампы, включенной в ту же сеть, немного уменьшается. Как объяснить это явление?
ЗДАНИЕ 2
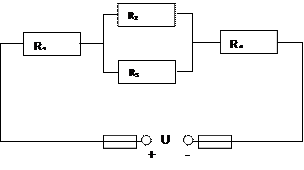
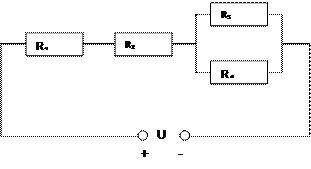
Цепь постоянного тока со смешанным соединением состоит из четырех резисторов. В зависимости от варианта заданы: схема цепи (по номеру рисунка), сопротивление резисторов R1, R2, R3, R4, напряжение U, ток I или мощность Р всей цепи. Определить: 1) эквивалентное сопротивление цепи Rэкв; 2) токи, проходящие через каждый резистор, I1, I2, I3, I4. Решение задачи проверить, применив первый закон Кирхгофа. Данные для своего варианта взять из таблицы.
Рис. 3 Рис. 4
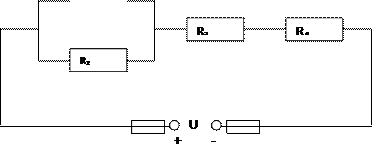
Определить силу тока в каждом элементе и напряжение на зажимах реостата, если Е1 =12 В, r1 = 1 Ом, Е2 = 6 В, r2 = 1,5 Ом и R = 20 Ом.
ЗАДАНИЕ 4.
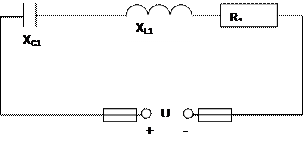
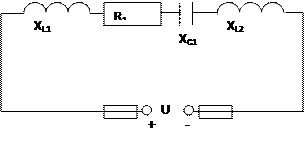
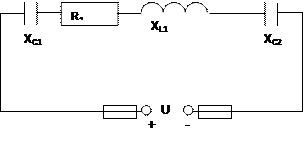
Для неразветвленной цепи переменного тока с активными, индуктивными и емкостными сопротивлениями определить величины, которые не должны в условиях задачи: 1) Z – полное сопротивление цепи, Ом; 2) I – ток цепи, А; 3) U – напряжение приложенное к цепи, В; 4) Φ – угол сдвига фаз между токами и напряжением; 5) S – полную, В∙А; Р – активную, Вт; Q – реактивную, вар, мощности цепи.
Построить в масштабе векторную диаграмму и кратко описать порядок ее построения, указав, в какую сторону и почему направлен каждый вектор. Числовые значения электрических величин, нужные для решения задачи, и номер рисунка даны в таблице. Проверить решение задачи, сравнивая значения приложенного напряжения U и угла сдвига фаз цепи φ, полученные расчетным путем или заданные в условиях, с результатами подсчета по векторной диаграмме. При расхождении найти ошибку. Рис. 0 Рис. 1
Рис. 2 Рис. 3
Контрольная работа для заочного отделения. Вариант № 3 ЗАДАНИЕ 1.
1. В какую сторону направлен постоянный электрический ток в металлическом проводнике относительно направления движения носителей заряда? 2. Как выражается в общем виде (формулой) при токе I напряжение на зажимах: а) электроприемника с сопротивлением R; с э.д.с. Е и внутренним сопротивлением r? б) источника электрической энергии с э.д.с. Е и внутренним сопротивлением r? 3. Почему уменьшаются потери энергии в трансформаторе, если его сердечник собирают из отдельных изолированных листов электротехнической стали?
ЗАДАНИЕ 2
Цепь постоянного тока со смешанным соединением состоит из четырех резисторов. В зависимости от варианта заданы: схема цепи (по номеру рисунка), сопротивление резисторов R1, R2, R3, R4, напряжение U, ток I или мощность Р всей цепи. Определить: 1) эквивалентное сопротивление цепи Rэкв; 2) токи, проходящие через каждый резистор, I1, I2, I3, I4. Решение задачи проверить, применив первый закон Кирхгофа. Данные для своего варианта взять из таблицы.
Рис. 3 Рис. 4
Два источника тока с э.д.с. 12 В и 8 В и внутренними сопротивлениями 4 Ом и 2 Ом, а также проводник сопротивлением 20 Ом соединены, как показано на рисунке. Определить силы тока в реостате и источниках тока.
ЗАДАНИЕ 4.
Для неразветвленной цепи переменного тока с активными, индуктивными и емкостными сопротивлениями определить величины, которые не должны в условиях задачи: 1) Z – полное сопротивление цепи, Ом; 2) I – ток цепи, А; 3) U – напряжение приложенное к цепи, В; 4) Φ – угол сдвига фаз между токами и напряжением; 5) S – полную, В∙А; Р – активную, Вт; Q – реактивную, вар, мощности цепи.
Построить в масштабе векторную диаграмму и кратко описать порядок ее построения, указав, в какую сторону и почему направлен каждый вектор. Числовые значения электрических величин, нужные для решения задачи, и номер рисунка даны в таблице. Проверить решение задачи, сравнивая значения приложенного напряжения U и угла сдвига фаз цепи φ, полученные расчетным путем или заданные в условиях, с результатами подсчета по векторной диаграмме. При расхождении найти ошибку. Рис. 0 Рис. 1
Рис. 2 Рис. 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.166.207 (0.006 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




 ЗАДАНИЕ 3.
ЗАДАНИЕ 3.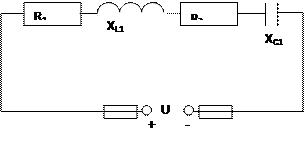
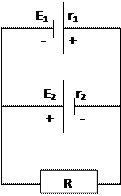 ЗАДАНИЕ 3.
ЗАДАНИЕ 3.


