
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выполнение арифметических операций
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами. Например, в десятичной системе числа записываются с помощью десяти всем хорошо известных цифр: 0, 1, 2 и т.д. Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных – не зависит. Самой распространенной из непозиционных систем счисления является римская. Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, т.е. в ней использовалось шестьдесят цифр. В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Наиболее распространенными в настоящее время позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная. Каждая позиционная система имеет определенный алфавит цифр и основание. В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения цифр соседних разрядов числа. Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских, цифр и имеет основание, равное 10, двоичная – две цифры и основание 2, восьмеричная – восемь цифр и основание 8, шестнадцатеричная – шестнадцать цифр (в качестве цифр используются и буквы латинского алфавита) и основание 16. Наиболее распространенной позиционной системой счисления является десятичная система. Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается трижды, причем самая правая обозначает пять единиц, вторая справа – пять десятков и, наконец, третья – пять сотен. Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.
Число в позиционных системах счисления записывается в виде суммы числового ряда степеней основания в данном случае 10), в качестве коэффициентов которых выступают цифры данного числа. В общем случае в десятичной системе запись числа А10, которое содержит n целых разрядов числа и m дробных разрядов числа, производится следующим образом: В двоичной системе основание равно 2, а алфавит состоит из двух цифр (0 и 1). Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1. В общем случае в двоичной системе запись числа А2, которое содержит n целых разрядов числа и m дробных разрядов числа, производится следующим образом: Возможно использование множества позиционных систем счисления, основание которых равно или больше 2. В системах счисления с основанием q (q-ичная система счисления) числа в развернутой форме записываются в виде суммы ряда степеней основания q с коэффициентами, в качестве которых выступают цифры 0, 1, q–1. Преобразование чисел, представленных в двоичной, восьмеричной и шестнадцатеричной системах счисления, в десятичную выполнить довольно легко. Для этого необходимо записать число в развернутой форме и вычислить его значение. Перевод чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную более сложен и может осуществляться различными способами. Алгоритм перевода целого десятичного числа в двоичное будет следующим: 1. Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор, пока не получим частное меньше делителя, т.е. меньше 2. 2. Получить искомое двоичное число, для чего записать полученные остатки в обратной последовательности. Алгоритм перевода десятичной дроби в двоичную будет следующим: 1. Последовательно выполнять умножение исходной десятичной дроби и получаемых дробей на основание системы (на 2) до тех пор, пока не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений.
2. Получить искомую двоичную дробь, записав полученные целые части произведения в прямой последовательности. Перевод чисел, содержащих и целую и дробную часть, производится в два этапа. Отдельно переводится по соответствующему алгоритму целая часть и отдельно – дробная. В итоговой записи полученного числа целая часть от дробной отделяется запятой.
Основные понятия и операции формальной логики. Логические выражения и их преобразование Логика – это наука о формах и способах мышления. Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира. Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны. Мышление всегда осуществляется в каких-то формах. Основными формами мышления являются понятие, суждение и умозаключение. Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта. Понятие имеет две стороны: содержание и объем. Содержание понятия составляет совокупность существенных признаков объекта. Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других объектов. Объем понятия определяется совокупностью предметов, на которые оно распространяется. Свое понимание окружающего мира человек формулирует в форме высказываний (суждений, утверждений). Высказывание строится на основе понятий и по форме является повествовательным предложением. Высказывания могут быть выражены не только с помощью естественных языков, но и с помощью формальных языков. Об объектах можно судить верно или неверно, т.е. высказывание может быть истинным или ложным. Истинным будет высказывание, в котором связь понятий правильно отражает свойства и отношения реальных вещей. Ложным высказывание будет в том случае, когда оно не соответствует реальной действительности. Конечно, иногда истинность того или иного высказывания является относительной. Истинность высказываний может зависеть от взглядов людей, от конкретных обстоятельств и т.д. Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними. Высказывание может быть либо истинно, либо ложно. Высказывание не может быть выражено повелительным или вопросительным предложением, т.к. оценка их истинности или ложности невозможна. На основании простых высказываний могут быть построены составные высказывания. Если истинность или ложность простых высказываний устанавливается в результате соглашения на основании здравого смысла, то истинность или ложность составных высказываний вычисляется с помощью использования алгебры высказываний. Умозаключения позволяют на основе известных фактов, выраженных в форме суждений, получать заключение, т.е. новое знание. Примером умозаключений могут быть геометрические доказательства. Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение. Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда, если умозаключение проводится в соответствии с правилами формальной логики, то оно будет истинным. В противном случае, можно придти к ложному умозаключению.
Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание. В алгебре высказываний суждениям (простым высказываниям) ставятся в соответствие логические переменные, обозначаемые заглавными буквами латинского алфавита; высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения «истина» (1) и «ложь» (0); над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания. Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не». Объединение двух (или нескольких) высказываний в одно с помощью союза «и» называется операцией логического умножения или конъюнкцией. Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны входящие в него простые высказывания. Функция логического умножения может принимать лишь два значения «истина» (1) и «ложь» (0). Значение логической функции можно определить с помощью таблицы истинности данной функции:
Объединение двух (или нескольких) высказываний с помощью союза «или» называется операцией логического сложения или дизъюнкцией. Составное высказывание, образованное в результате логического сложения (дизъюнкции), истины но тогда, когда истинно хотя бы одно из входящих в него простых высказываний. Значение логической функции можно определить с помощью таблицы истинности данной функции:
Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным. Таблица истинности функции логического отрицания:
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую войдут логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составных высказываний в виде логических выражений на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними. При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий. Во-первых, необходимо определить количество строк в таблице истинности, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных n, то: Количество строк = 2n. Во-вторых, необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций. В-третьих, необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести возможные наборы значений исходных логических переменных. В-четвертых, необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности. Теперь мы можем определить значение логической функции для любого набора значений логических переменных. Логические выражения, у которых таблицы истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=». Для доказательства равносильности необходимо составить таблицы истинности для левой и правой частей равенства, затем сравнить полученные результаты. Законы логики отражают наиболее важные закономерности логического мышления. Закон тождества. Всякое высказывание тождественно самому себе: Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным. Если высказывание А – истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно. Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение истина. Закон двойного отрицания. Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание. Кроме логических законов, важное значение для выполнения преобразований логических выражений имеют правила алгебраических преобразований. Правило коммутативности. В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения. Правило ассоциативности. Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять. Правило дистрибутивности. В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 40; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.6.75 (0.016 с.) |
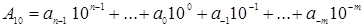 .
.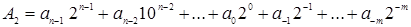 .
.



