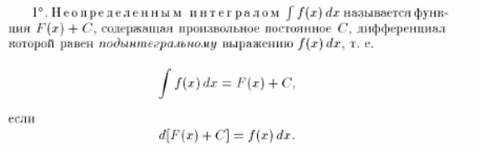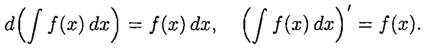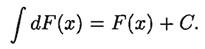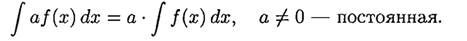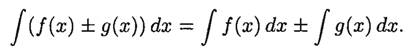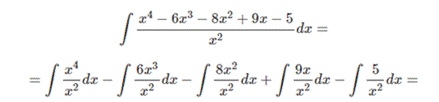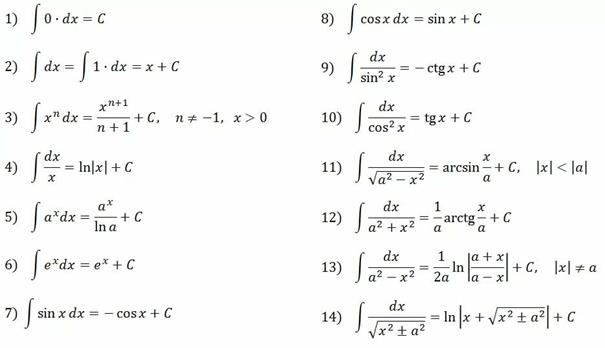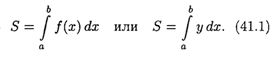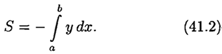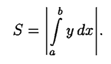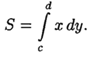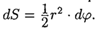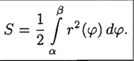Неопределенный интеграл. Основные свойства.

Неопределенный интеграл. Основные свойства.

 

Первообразная. Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство F′(x) = f(x) для любого х из заданного промежутка.

Неопределенный интеграл. Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается ʃ f(x)dx = F(x) + C

Отыскивание неопределенного интеграла называют интегрированием функции.

 

Таблица интегралов:

Свойства неопределенного интеграла:

1. Дифференциал от неопределенного интеграла равен подынте­гральному выражению, а производная неопределенного интеграла рав­на подынтегральной функции:

 

2. Неопределенный интеграл от дифференциала некоторой функ­ции равен сумме этой функции и произвольной постоянной:

3. Постоянный множитель можно выносить за знак интеграла:

4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций:

Методы интегрирования: метод разложения.

Формула метода разложения интегралов имеет вид:

Стоит отметить, что функции f1(x) и f2(x) подбирают таким образом, чтобы интегралы от них брались непосредственно.(это значит, что   в интеграле присутствуют табличные элементарные функции, либо функции, сводящиеся к таким путём элементарных преобразований.)

ПРИМЕР:

Методы интегрирования: метод разложения, интегрирование по частям.

Интегрирование по частям для неопределенных интегралов.

Пусть u = u(x) и v = v(x) – функции, имеющие непрерывные производные. Тогда d(uv) = udv + vdu. Интегрируя это равенство, получим

∫ d(uv)= ∫ udv + ∫ vdu.

Полученная формула называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла ∫ udv к вычислению интеграла ∫ vdu.

Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей u и dv; затем, после нахождения v и du, используется формула интегрирования по частям.

 

Типы интегралов, которые можно вычислять методом интегрирования по частям:

1) ∫ P(x) e^kx dx, ∫P(x)sinkx dx, ∫P(x)coskx dx.

P(x) – многочлен, k – число. Удобно положить u=P(x), а за dv обозначить остальные сомножители.

 

2) ∫ P(x)arcsinx dx, ∫ P(x)arccosx dx, ∫ P(x)lnx dx, ∫P(x)arctgx dx, ∫ P(x)arcctgx dx.

Удобно положить P(x)dx=dv, а за u обозначить остальные сомножители.

 

3) ∫ e^(ax)sinbx dx, ∫ e^(ax)coskx dx, где a и b – числа. За u можно принять функцию u = e^ax.

Метод разложения. (см. билет №2)

Таблица простейших интегралов.

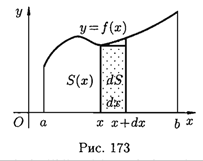
Прямоугольные координаты

Площадь криволинейной трапеции, расположенной «выше» оси абсцисс (f(х)⩾ 0), равна соответствующему определенному интегралу:

Пусть криволинейная трапеция ограничена линиями у = f(x)⩾ 0, х = а, х =b, y = 0 (см. рис.173). Для нахождения площади S этой трапеции проделаем следующие операции:

1. Возьмем произвольное х ϵ [а; Ь] и будем считать, что S=S(х).

2. Дадим аргументу х приращение Δх = dx (х + Δх ϵ [а; Ь]). Функция S = S(х) получит приращение ΔS, представляющее собой площадь «элементарной криволинейной трапеции» (на рисунке она выделена).

Дифференциал площади dS есть главная часть приращения ΔS при Δх → 0, и, очевидно, он равен площади прямоугольника с основанием dx и высотой у: dS = у*dx.

3. Интегрируя полученное равенство в пределах от х = а до х = b, получаем:

Отметим, что если криволинейная трапеция расположена «ниже» оси Ох (f(х) < 0), то ее площадь может быть найдена по формуле

Формулы (41.1) и (41.2) можно объединить в одну:

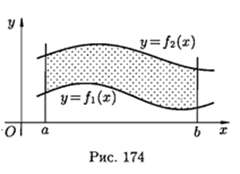
Площадь фигуры, ограниченной кривыми у = f₁(x) и y= f₂(x), прямыми x = а и х = b (при условии f₂(x) ⩾ f₁(x)) (см. рис. 174), можно найти по формуле

Если плоская фигура имеет «сложную» форму (см. рис. 175), то прямыми, параллельными оси Оу, ее следует разбить на части так, чтобы можно было бы применить уже известные формулы.

Если криволинейная трапеция ограничена прямыми у = с и у = d, осью Оу и непрерывной кривой х = ϕ(у)⩾ 0 (см. рис. 176), то ее площадь находится по формуле

И, наконец, если криволинейная трапеция ограничена кривой, заданной параметрически

прямыми х = α и х = β и осью Ох, то площадь ее находится по формуле

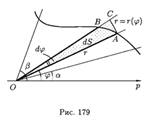
где α и β определяются из равенств х(α) = а и х(β) = b.

Полярные координаты

Найдем площадь S криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией r = r(ϕ) и двумя лучами ϕ= α и ϕ= β (α <β), где r и ϕ- полярные координаты (см. рис. 179).

1. Будем считать часть искомой площади S как функцию угла ϕ, т. е. S=S(ϕ), где α ≤ϕ ≤β (если ϕ= α, то S(α) = 0, если ϕ= β, то S(β) = S).

2. Если текущий полярный угол ϕ получит приращение Δϕ= dϕ, то приращение площади ΔS равно площади «элементарного криволинейного сектора» ОАВ.

Дифференциал dS представляет собой главную часть приращения ΔS при dϕ→0 и равен площади кругового сектора ОАС (на рисунке она заштрихована) радиуса r с центральным углом dϕ. Поэтому

3. Интегрируя полученное равенство в пределах от ϕ= α до ϕ= β, получим искомую площадь

Произведение матриц.

Т.е. элемент i-й строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k–го столбца матрицы В.

Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А*Е=Е А=А, где А-квадратная матрица, Е- единичная матрица того же размера.

Матрицы А и В называются перестановычными, если АВ=ВА.

Если, конечно, написанные суммы и произведения матриц имеют смысл.

Для операции транспонирования верны свойства:

Умножение матрицы на число

Произведением матрицы А(m*n)=на число к называется матрица В(m*n)= такая, что. Записывают В=к*А

Неопределенный интеграл. Основные свойства.

 

Первообразная. Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство F′(x) = f(x) для любого х из заданного промежутка.

Неопределенный интеграл. Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается ʃ f(x)dx = F(x) + C

Отыскивание неопределенного интеграла называют интегрированием функции.

 

Таблица интегралов:

Свойства неопределенного интеграла:

1. Дифференциал от неопределенного интеграла равен подынте­гральному выражению, а производная неопределенного интеграла рав­на подынтегральной функции:

 

2. Неопределенный интеграл от дифференциала некоторой функ­ции равен сумме этой функции и произвольной постоянной:

3. Постоянный множитель можно выносить за знак интеграла:

4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций: