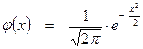Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка статистических гипотезСодержание книги
Поиск на нашем сайте Рассмотрим гипотезу о том, что генеральная совокупность, из которой извлечена выборка, распределена по нормальному закону. Назовём эту гипотезу нулевой и проверим её с помощью критерия χ2 Пирсона. Для этого сравним эмпирические частоты ni (полученные в результате проведённого опыта) и теоретические частоты niT, вычисленные в предположении нормального закона распределения. Если эмпирические частоты сильно отличаются от теоретических, то проверяемую гипотезу следует отвергнуть, в противном случае – принять. Для проверки нулевой гипотезы в качестве критерия, который характеризовал бы степень расхождения между эмпирическими и теоретическими частотами, рассмотрим случайную величину По таблице χ2 Пирсона (приложение 2) находят критическое значение χ2, которое зависит от двух параметров k и α, где α – уровень значимости, а k – число степеней свободы. Число степеней свободы находится по формуле k = m – r – 1, где m – число интервалов в распределении выборки, r – число параметров распределения (для нормального распределения r = 2, для показательного распределения r = 1, для равномерного r = 2 и т.д.). После нахождения критического значения χ2 из таблицы, необходимо сравнить это значение с наблюдаемым
Проверим выполнимость нормального распределения для выборки примера 1.
Из приведённых в примере 1 расчётов М = 13,2, ϭ = 1,9, тогда Число степеней свободы k = m – r – 1 = 6 – 2 – 1 = 3, уровень значимости возьмём α = 0,05 и по таблице (приложение 2) найдём критическое χ2 (0,05; 3) = 7,8. 7,8 < 7,889 => гипотеза о нормальном распределении не подтверждается. Пример расчетной задачи Известны данные о пределе текучести у 50 марок стали (кг/мм2): 71 77 76 76 47 36 50 49 62 40 106 109 109 110 111 68 88 141 136 129 126 96 100 95 118 107 120 114 113 123 94 84 73 107 94 107 99 100 104 88 84 94 142 98 77 88 94 76 84 125 Построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) медиану; б) моду; в) среднее арифметическое; г) дисперсию; д) среднее квадратичное отклонение. Проверить гипотезу о нормальном распределении выборки, используя метод χ2 Пирсона. РЕШЕНИЕ 1. Среди данных определим самое маленькое значение и самое большое: xmin = 36, xmax = 142. 2. Вычислим ширину интервалов статистического распределения h:
3.Составим статистическое распределение:
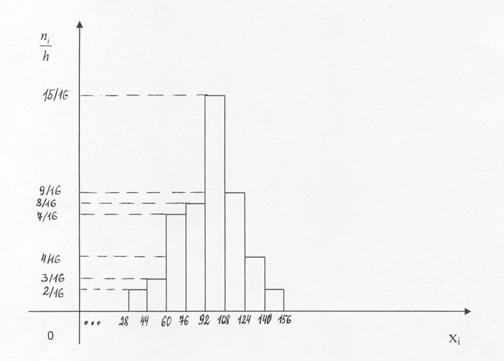
4. Построим полигон и гистограмму полученного статистического распределения.
5. Найдём основные математические характеристики: а) Мода М0 = 100, т.к. это значение x’i соответствует наибольшей частоте ni = 15. б) Медиана Ме = в) Среднее арифметическое М:
г) Дисперсия
д) Среднее квадратическое отклонение
6. Проверим гипотезу о нормальном распределении выборки. М = 95, ϭ = 26, h = 16, n = 50 => Составим таблицу:
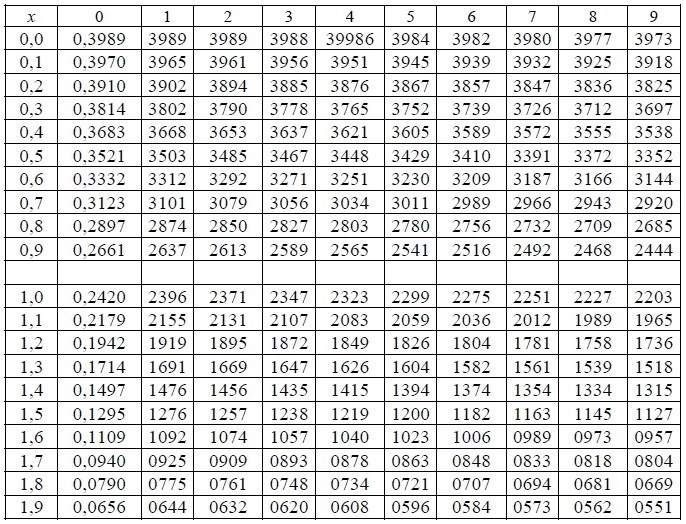
u 1 = Заполняя четвёртый столбец таблицы, φ(ui) находим по таблице значений дифференциальной функции Лапласа, используя приложение 1. Число степеней свободы k = m – 3 = 8 – 3 = 5, где m – это число интервалов в полученном распределении нашей выборки. По уровню значимости α = 0,05 и числу степеней свободы из таблицы критических точек распределения Пирсона «хи-квадрат» (приложение 2) находим значение χ2 = 11, 07. Сравниваем значения
ОТВЕТ: а) М0 = 100; б) Ме = 92; в) М =95; г) D = 680,36; д) Контрольная работа Вариант 0 Известны данные о посевных площадях картофеля (тыс. гектаров) по районам Курганской области:
Построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) медиану; б) моду; в) среднее арифметическое; г) дисперсию; д) среднее квадратичное отклонение. Проверить гипотезу о нормальном распределении выборки, используя метод χ2 Пирсона.
Вариант 1 На 10 мая 1982 года по районам Пермской области было посеяно яровых культур (в процентах к площади):
Построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) медиану; б) моду; в) среднее арифметическое; г) дисперсию; д) среднее квадратичное отклонение. Проверить гипотезу о нормальном распределении выборки, используя метод χ2 Пирсона.
Вариант 2 При сверлении отверстий одним и тем же сверлом и последующем измерении диаметров, получены следующие данные (в мм):
Построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) медиану; б) моду; в) среднее арифметическое; г) дисперсию; д) среднее квадратичное отклонение. Проверить гипотезу о нормальном распределении выборки, используя метод χ2 Пирсона.
Вариант 3 Имеются данные о размерах основных фондов (в млн. руб.) 30 предприятий:
Построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) медиану; б) моду; в) среднее арифметическое; г) дисперсию; д) среднее квадратичное отклонение. Проверить гипотезу о нормальном распределении выборки, используя метод χ2 Пирсона.
Вариант 4 Имеются данные интервалов между разрядами нейрона зрительной коры кролика в м/сек:
Построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) медиану; б) моду; в) среднее арифметическое; г) дисперсию; д) среднее квадратичное отклонение. Проверить гипотезу о нормальном распределении выборки, используя метод χ2 Пирсона.
Вариант 5 Имеются данные о величине латентного периода (в сек.) механического ответа при даче светового сигнала в первом предъявлении:
Построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) медиану; б) моду; в) среднее арифметическое; г) дисперсию; д) среднее квадратичное отклонение. Проверить гипотезу о нормальном распределении выборки, используя метод χ2 Пирсона.
Вариант 6 Имеются данные измерения длины плеча (в мм) мухоловки пеструшки на 5-й день жизни:
Построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) медиану; б) моду; в) среднее арифметическое; г) дисперсию; д) среднее квадратичное отклонение. Проверить гипотезу о нормальном распределении выборки, используя метод χ2 Пирсона.
Вариант 7 Имеются данные измерения (в сек.) скорости механического ответа при комплексном свето-звуко-тактильном раздражении:
Построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) медиану; б) моду; в) среднее арифметическое; г) дисперсию; д) среднее квадратичное отклонение. Проверить гипотезу о нормальном распределении выборки, используя метод χ2 Пирсона.
Вариант 8 Имеются данные измерения величин интенсивности порогового раздражения глаз при длительности дачи света в 0,002 сек:
Построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) медиану; б) моду; в) среднее арифметическое; г) дисперсию; д) среднее квадратичное отклонение. Проверить гипотезу о нормальном распределении выборки, используя метод χ2 Пирсона.
Вариант 9 Имеются данные измерения латентных периодов механического ответа (в сек.) при даче светового сигнала во втором предъявлении:
Построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) медиану; б) моду; в) среднее арифметическое; г) дисперсию; д) среднее квадратичное отклонение. Проверить гипотезу о нормальном распределении выборки, используя метод χ2 Пирсона.
Вопросы к экзамену 1. Понятие о статистической совокупности, выборке. Статистическое распределение выборки. 2. Полигон и гистограмма. Эмпирическая функция распределения. 3. Характеристики эмпирического распределения (мода, медиана, средняя выборочная, среднее квадратическое отклонение) и их вычисление. 4. Оценки параметров генеральной совокупности по её выборке. Точность оценки параметров. 5. Проверка статистических гипотез. Сравнение эмпирических распределений с нормальным и другими теоретическими распределениями. 6. Понятие о корреляционной зависимости, о функции регрессии, о линиях регрессии.
Примеры тестовых заданий на проверку теоретических знаний 1. Ломаная, которая соединяет точки с координатами а) гистограммой; б) полигоном; в) медианой; г) модой. 2. Совокупность прямоугольников, основаниями которых являются интервалы значений наблюдаемой величины, а высотой величина а) гистограммой; б) полигоном; в) медианой; г) модой. 3. Значение наблюдаемого признака, который встречается чаще всего, т.е. обладает наибольшей частотой называется … а) гистограммой; б) полигоном; в) медианой; г) модой. 4. Значение наблюдаемого признака, которое находится посередине статистического распределения выборки или совокупности, называется … а) гистограммой; б) полигоном; в) медианой; г) модой. 5. Среднее арифметическое статистического распределения вычисляется по формуле: а) σ = 6. Среднее квадратическое отклонение статистического распределения вычисляется по формуле … а) σ = 7. Некоторая совокупность объектов, которые являются однородными по структуре и изучаются по одному и тому же качественному или количественному признаку, называется... а) генеральной статистической совокупностью; б) выборкой; в) модой; г) медианой. 8. Для изучения свойств всей генеральной совокупности чаще всего выбирают лишь часть объектов, эта часть называется … а) генеральной статистической совокупностью; б) выборкой; в) модой; г) медианой. 9. Если выделить некоторые количественные или качественные признаки для конкретной выборки и провести изучение выборки по выделенным признакам, то их значение принято называть … а) вариантой; б) выборкой; в) модой; г) медианой. 10. Метод χ2 проверки гипотезы о нормальном законе распределения выборки носит имя … а) Колмогорова; б) Пирсона; б) Фишера; г) Стьюдента Литература 1. Баврин И. И. Высшая математика. – М.: Издательский центр «Академия», 2002. 2. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие – 12-е изд., переаб. – М.: Высшее образование, 2006. 3. Ильин В. А. Высшая математика. – М.: Проспект, 2002. 4. Ильин В. А., Куркина А. В. Высшая математика. – М., 2004. 5. Лобоцкая Н. Л. Основы высшей математики. – Минск: Высшая школа, 1978. 6. Маркович Э. С. Курс высшей математики с элементами теории вероятностей и математической статистики. – М.: Высшая школа, 1982. 7. Суходольский Г. В. Основы математической статистики для психологов.
Приложение 1 Таблица значений функции
Таблица критических точек распределения Пирсона «хи-квадрат»
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

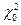 =
= 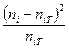 . Критерий Пирсона позволяет ответить на вопрос, объяснимы ли расхождения между частотами только случайными факторами, например, связанные с ограниченным числом наблюдений, или это связано с неправильным выбором теоретического закона распределения. Но, как и любой другой критерий, он не доказывает справедливости гипотезы, а лишь устанавливает её согласие или не согласие с экспериментальными данными на принятом уровне значимости. Обычно уровень значимости выбирают α = 0,05, или 0, 01, или 0,1. То есть, с вероятностью 0,95 (или 0,99, или 0,9) можно гарантировать принятие или опровержение гипотезы.
. Критерий Пирсона позволяет ответить на вопрос, объяснимы ли расхождения между частотами только случайными факторами, например, связанные с ограниченным числом наблюдений, или это связано с неправильным выбором теоретического закона распределения. Но, как и любой другой критерий, он не доказывает справедливости гипотезы, а лишь устанавливает её согласие или не согласие с экспериментальными данными на принятом уровне значимости. Обычно уровень значимости выбирают α = 0,05, или 0, 01, или 0,1. То есть, с вероятностью 0,95 (или 0,99, или 0,9) можно гарантировать принятие или опровержение гипотезы.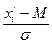
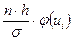
 . Значения четвёртого столбца находим по таблице значений функции Лапласа (приложение 1).
. Значения четвёртого столбца находим по таблице значений функции Лапласа (приложение 1).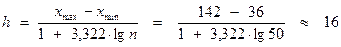 , n – объём выборки, т.е. количество измерений данных по условию задачи.
, n – объём выборки, т.е. количество измерений данных по условию задачи.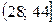
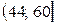
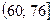
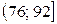
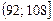
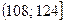
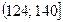
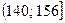
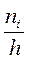
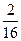
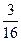
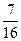
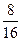
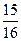
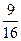
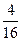
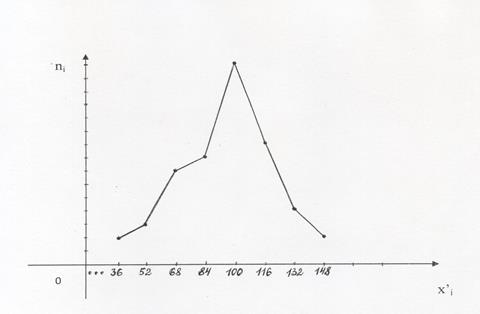
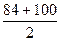 = 92, т.к. количество интервалов в распределении чётное (k = 8), то в качестве медианы берём среднее арифметическое двух центральных значений x’i.
= 92, т.к. количество интервалов в распределении чётное (k = 8), то в качестве медианы берём среднее арифметическое двух центральных значений x’i.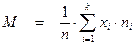
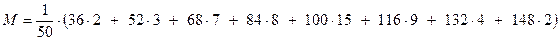 =
= 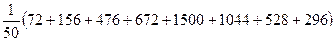 =
= 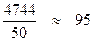
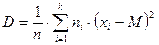
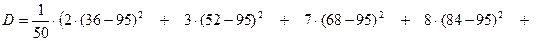
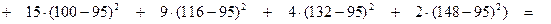
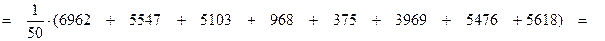
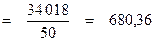 ;
; 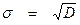
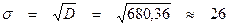
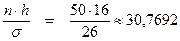
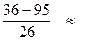 - 2,27; u 2 =
- 2,27; u 2 = 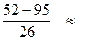 - 1,65; u 3 =
- 1,65; u 3 = 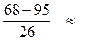 - 1,04 и т.д.
- 1,04 и т.д. 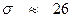
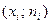 или
или 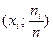 называется …
называется …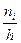 или
или 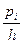 , называется …
, называется …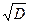 =
= 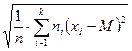 ; б) n =
; б) n = 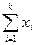 ; в) М =
; в) М = 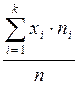 ; г) P(A) =
; г) P(A) = 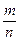 .
.