Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как формируются силы, определяющие величину скорости звенаи направление его движения.Содержание книги
Поиск на нашем сайте Скорости и ускорения ведомых звеньев механизма могут быть определены методами планов, кинематических диаграмм и аналитическими. Во всех случаях в качестве исходных должны быть известны: схема механизма при определенном положении ведущего звена, его скорость и ускорение. Метод планов. Построение планов скоростей и ускорений проводится на основе последовательного составления векторных уравнений для всех групп, входящих в механизм, начиная с ведущего звена. Для определения полной картины скоростей любого звена, входящего в группу, достаточно знать линейные скорости двух точек этого звена или линейную скорость одной точки и угловую скорость звена. Так как скорости конечных элементов звеньев групп известны, то необходимо выбрать общую для двух звеньев точку и записать два уравнения для определения скорости этой точки. Для групп первого, второго и четвертого видов это постоянная точка — центр средней вращательной пары группы, для других — мгновенная точка на одном звене, совпадающая в данный момент с центром конечной вращательной пары другого звена.
В качестве примера рассмотрим построение планов скоростей и ускорений группы второго класса второго вида. План скоростей. В этой группе (рис. 2.3, а) полагаем, что скорости примыкающих звеньев 1 и 4 заданы. Следовательно, скорость точки В2, принадлежащей звену 2, равна скорости точки Blt принадлежащей звену 1, т. е.
Рассмотрим движение звена 2 относительно звена 1. Эти звенья образуют вращательную пару, поэтому на основании теоремы о сложении скоростей в сложном движении скорость точки С на звене 2 складывается из скорости
где vCB = Теперь определим скорость точки С, отнеся ее к третьему звену. Звено 3 образует со звеном 4 поступательную пару, поэтому скорость точки С3 можно представить как сумму двух скоростей: скорости Vc4 точки С4, совпадающей с точкой С3 и принадлежащей среде переноса (в данном случае примыкающему звену 4), и скорости точки С3 относительно точки С4 в поступательном движении I звена 3 относительно звена 4 — Vc3c4, т. е.
Точку С4 расположим на плоскости, жестко связанной со звеном 4. Зная закон движения этого звена, можно найти мгновенный центр вращения (МЦВ) и при известных расстоянии его от точки С4 и угловой скорости ω4 определить величину и направление скорости этой точки. Систему уравнений (2.6) и (2.7) решим графически в выбранном масштабе
Далее из полюса р0 плана скоростей параллельно вектору Vc4 (рис. 2.3, а) откладываем отрезок
а направление ее определится мысленным переносом вектора относительной скорости Vcb — отрезка bc плана скоростей в точку С на плане положения группы. Пользуясь планом скоростей, можно найти скорость любой точки на звене. Скорость точки S на втором звене определится из условия представления сложного движения звена 2 как поступательного со скоростью VB и вращательного вокруг точки В, а также как поступательного со скоростью Vc и вращательного вокруг точки С:
Решая эту систему графически, определяют точку s — конец вектора Из построения следует, что треугольник csb на плане скоростей подобен треугольнику CSB на плане положений группы и повернут относительно него на 90°. Правильность построения определяется одинаковым порядком букв при обходе контура звена и контура относительных скоростей на плане скоростей в одном и том же направлении. План ускорений. Исходными данными для построения плана ускорений являются план положения группы, план скоростей (рис. 2.3, а, б) и ускорения звеньев, примыкающих к данной группе. При построении плана ускорений полностью применимы рассуждения, использованные при решении задачи об отыскании скоростей звеньев. Ускорение точки В2 известно, так как она совпадает с точкой В1 т. е. Для нахождения ускорения любой точки звеньев 2 и 3 дополнительно надо знать ускорение хотя бы одной точки на каждом из этих звеньев. В качестве такой точки следует использовать центр шарнира С, являющийся общей точкой для звеньев 2 и 3. Рассматривая вращательное движение звена 2 вокруг точки В и поступательное — звена 3 относительно звена 4, записываем следующие векторные уравнения:
Систему уравнений решим графически. На чертеже (рис. 2.3, б) обозначим полюс плана ускорений рa и выберем масштаб построения плана Откладываем от полюса ра параллельно вектору ускорения ав отрезок pab =
Из точки b плана ускорений проводим линию действия ускорения Из точки п перпендикулярно к отрезку bп проводим линию действия тангенциального ускорения
Пересечение линий действия Из плана ускорения получим также величины и направления векторов относительных ускорений Угловое ускорение звена 2 определится по формуле
Направление ε2 устанавливается путем мысленного переноса вектора пс в точку С и определения направления вращения звена 2 вокруг точки В под влиянием этого вектора. Пользуясь планом ускорений, можно найти ускорение любой точки на звене 2 и 3. Например, требуется определить ускорение точки S на звене 2. На основании известного положения о подобии фигур звена и плана относительных ускорений строим на отрезке bc плана ускорений треугольник csb, подобный треугольнику CSB на звене 2, соблюдая при этом одинаковую последовательность расположения букв при обходе контуров этих треугольников в одном направлении. Соединяя полученную в результате построения точку s с полюсом ра, получаем отрезок pas, определяющий в масштабе ускорение точки S: Метод кинематических диаграмм. В тех случаях, когда необходимо установить законы изменения скоростей и ускорений за определенный промежуток времени движения звена, применяют метод кинематических диаграмм, который базируется на графическом дифференцировании и интегрировании. Используя график движения ведомого звена по времени s = s(t) или
При выполнении графического дифференцирования можно оперировать не только касательными, но и хордами, проводить которые удобнее (рис. 2.4). Тогда значение средней скорости на элементарном участке пути может быть выражено в виде где Δs и Δt — элементарные перемещение и время; а — угол, образованный хордой и осью абсцисс графика s = s (t). На участках графика (рис. 2.4, а), соответствующих делениям по оси абсцисс, заменяем кривую отрезками прямой. Приняв полученную ломаную линию за график пути, строим соответствующий ему график скорости. Для этого слева от начала координат на расстоянии
Для построения графика скорости v = v (t) следует полученные отрезки отложить параллельно оси ординат нового графика в серединах соответствующих участков и соединить полученные точки плавной кривой. Построение графика ускорений по известному графику скорости следует проводить в таком же порядке, как и описанное выше построение графика скорости по известному графику пути. В общем случае при дифференцировании графика v = v(t) получают только тангенциальную составляющую ускорения, так как Рис.. Кинематические диаграммы Обозначив через На полюсное расстояние, можно по аналогии с определением масштаба графика скорости получить масштаб графика ускорения
График перемещений по известному графику скорости или график скорости при заданном графике ускорения можно построить с помощью графического интегрирования. При интегрировании построение производят в порядке, обратном тому, какой принят при дифференцировании. На отдельных участках графика v = v (t) принимается постоянная средняя скорость (штриховые линии). Величины отрезков, определяющих скорости, сносятся на ось ординат. Точ Графическое интегрирование: а – график скорости; б – график перемещений Аналитический метод. Этот метод позволяет определять скорости и ускорения с более высокой точностью. Обычно применяют метод последовательного дифференцирования функции перемещения точки, скорость и ускорение которой необходимо определить. Функцию перемещения s = s (t) или s = s (φ) можно получить из геометрических соображений, как, например, это сделано для кривошипно-ползунного механизма — формула (2.5), а ее скорость и ускорение — путем дифференцирования уравнений (2.3). Дифференцируя уравнения (2.3) по обобщенной координате φ1 (углу поворота ведущего звена), получают не истинную угловую скорость, а безразмерную величину
Определим значение и подставим его в первое уравнение, с учетом формулы (2.4) получим значение
При вторичном дифференцировании уравнений (2.3) с использованием понятия аналога углового ускорения, представляющего вторую производную по углу поворота ведущего звена
Из уравнения (2.19) получим значение Получив значения угловых скоростей и ускорений, можно определить скорость и ускорение любой точки звеньев механизма. В тех случаях, когда
Раскладывая в ряд радикал, входящий в формулу (2.20) по биному Ньютона и ограничиваясь его первыми двумя членами, получим
После дифференцирования скорость Vc и ускорение
Пример. Построить план скоростей и ускорений механизма поперечно-строгального станка (рис. 2. 6,а), у которого В результате структурного анализа устанавливаем в механизме наличие группы пятого вида — звенья 4 (ползун) и 5 (резцовая головка), образующие кинематические пары D4, Е (внешние), D5 (внутреннюю), и третьего вида — звенья 2 (ползун) и 3 (кулиса), образующие кинематические пары В2, С (внешние), В3 (внутреннюю). Для отыскания скоростей звеньев 2 и 3 определяем скорость общей точки на этих двух звеньях, совпадающей с центром вращательной пары. Такой точкой будет точка В3 на звене 3, совпадающая в данный момент с точкой В2. Скорость точки В2 , являющейся общей для ведущего звена (палец кривошипа) и звена 2 (внешняя пара), определяем из условия Скорость точки С, принадлежащей стойке, равна нулю. Скорость точки В3 звена 3 определим через известные скорости точек звеньев, примыкающих к звену 3, — точки В2 на звене 2 и точки С на звене 0: Выбираем масштаб плана скоростей Угловая скорость
Рис. Кинематический анализ механизма поперечно-строгального станка Скорость центра вращательной пары D4, являющейся внешней для группы 4 —5, равна скорости точки D3 звена 3. Из подобия плана относительных скоростей плану звена
Скорость точки Do на стойке равна нулю;
Через точки d4 и d0 плана скоростей проводим линию действия скорости
На основании аналогичных рассуждений строится план ускорений механизма. Векторные уравнения для определения ускорения точки В3 имеют вид
Ускорение точки В2 как совпадающей с точкой В1 пальца кривошипа
Откладываем в выбранном масштабе Величины нормального ускорения
Эти ускорения в виде соответствующих отрезков
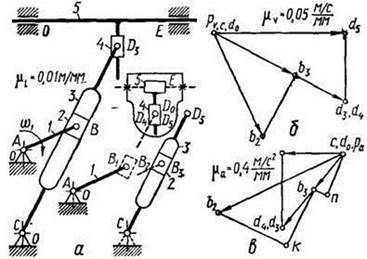
Угловое ускорение третьего звена по формуле, аналогичной формуле (2.13), Из подобия плана относительных ускорений плану звена определим ускорение
и в масштабе Для определения ускорения
Кориолисовы ускорения На пересечении указанных линий определится положение точки d5, и, следовательно, полное ускорение
|
||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.5 (0.048 с.) |

 При составлении векторных уравнений следует четко установить точки, скорости которых используются как скорости в переносном движении. Если звенья группы образуют поступательные кинематические пары, то необходимо использовать точки, принадлежащие направляющим звеньям.
При составлении векторных уравнений следует четко установить точки, скорости которых используются как скорости в переносном движении. Если звенья группы образуют поступательные кинематические пары, то необходимо использовать точки, принадлежащие направляющим звеньям.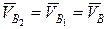 . Угловая скорость звена 3, образующего поступательную пару со звеном 4, равна заданной угловой скорости звена 4, т. е.
. Угловая скорость звена 3, образующего поступательную пару со звеном 4, равна заданной угловой скорости звена 4, т. е. 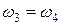 . Следовательно, для отыскания скоростей второго звена достаточно определить, кроме известной скорости точки В, скорость еще одной точки, а для третьего звена, кроме известной угловой скорости
. Следовательно, для отыскания скоростей второго звена достаточно определить, кроме известной скорости точки В, скорость еще одной точки, а для третьего звена, кроме известной угловой скорости 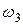 , также скорость какой-либо одной точки. Для решения этой задачи следует рассмотреть движение общей для этих двух звеньев точки С — центра средней вращательной пары.
, также скорость какой-либо одной точки. Для решения этой задачи следует рассмотреть движение общей для этих двух звеньев точки С — центра средней вращательной пары.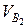 переносного (поступательного) движения звена со скоростью vB и скорости
переносного (поступательного) движения звена со скоростью vB и скорости 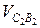 относительного (вращательного) движения звена 2 вокруг точки В:
относительного (вращательного) движения звена 2 вокруг точки В: (2.6)
(2.6) .
.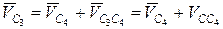 . (2.7)
. (2.7) на плане скоростей (рис. 2.3, б). Откладываем от полюса рv параллельно вектору скорости точки В отрезок рvc4 =
на плане скоростей (рис. 2.3, б). Откладываем от полюса рv параллельно вектору скорости точки В отрезок рvc4 = 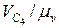 (мм) и через конец этого отрезка проводим прямую, являющуюся линией действия вектора vСB. Эта прямая перпендикулярна к линии ВС.
(мм) и через конец этого отрезка проводим прямую, являющуюся линией действия вектора vСB. Эта прямая перпендикулярна к линии ВС.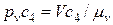 (мм). Через конец этого отрезка (точку C4) проводим прямую, параллельную направляющей поступательной пары D, являющейся линией действия вектора относительной поступательной скорости
(мм). Через конец этого отрезка (точку C4) проводим прямую, параллельную направляющей поступательной пары D, являющейся линией действия вектора относительной поступательной скорости 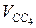 .Так как
.Так как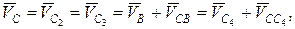 векторные суммы определяются точкой пересечения линий действия относительных скоростей. Точку пересечения этих линий обозначим С, абсолютная скорость точки С определится из условия
векторные суммы определяются точкой пересечения линий действия относительных скоростей. Точку пересечения этих линий обозначим С, абсолютная скорость точки С определится из условия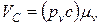 . Из плана скоростей получим также величины и направления векторов относительных скоростей: вращательной Vcb — отрезок bc и поступательной
. Из плана скоростей получим также величины и направления векторов относительных скоростей: вращательной Vcb — отрезок bc и поступательной 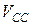 — отрезок с4с. Угловая скорость второго звена
— отрезок с4с. Угловая скорость второго звена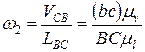 , (2.8)
, (2.8)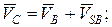
 . (2.9)
. (2.9)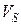 .
.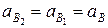 , угловое ускорение звена 3 известно, так как оно образует со звеном 4 поступательную пару, т. е. ε3 = ε4.
, угловое ускорение звена 3 известно, так как оно образует со звеном 4 поступательную пару, т. е. ε3 = ε4.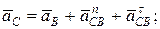
 (2.10)
(2.10)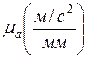 .
.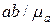 (мм). Нормальное ускорение
(мм). Нормальное ускорение 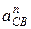 точки С в относительном движении направлено от точки С вдоль звена 2 к точке В; величину его, исходя из построенного плана скоростей, определим по формуле
точки С в относительном движении направлено от точки С вдоль звена 2 к точке В; величину его, исходя из построенного плана скоростей, определим по формуле . (2.11)
. (2.11)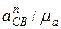 .
.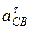 .Далее из полюса ра проводим линию параллельно известному направлению ускорения
.Далее из полюса ра проводим линию параллельно известному направлению ускорения  , () и откладываем отрезок
, () и откладываем отрезок 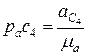 . Ускорение Кориолиса (поворотное ускорение)
. Ускорение Кориолиса (поворотное ускорение) откладываем на плане ускорения в виде отрезка c4k =
откладываем на плане ускорения в виде отрезка c4k = 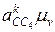 (мм). Направление указанного отрезка определяется путем поворота вектора относительной скорости с4с на 90° в сторону вращения среды поворота — звена 4. Из точки k проводим линию действия ускорения a'cc4, параллельную направляющей поступательной пары, т. е. перпендикулярно к вектору ускорений
(мм). Направление указанного отрезка определяется путем поворота вектора относительной скорости с4с на 90° в сторону вращения среды поворота — звена 4. Из точки k проводим линию действия ускорения a'cc4, параллельную направляющей поступательной пары, т. е. перпендикулярно к вектору ускорений 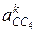 .
.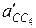 , определит положение точки с.
, определит положение точки с.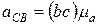 (м/с2) и
(м/с2) и  (м/с2).
(м/с2). (2.13)
(2.13) .
.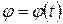 , определяют скорость как первую производную пути по времени:
, определяют скорость как первую производную пути по времени: 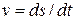 , или
, или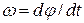 . Производные пропорциональны тангенсу угла наклона касательной в точках кривой графика перемещений.
. Производные пропорциональны тангенсу угла наклона касательной в точках кривой графика перемещений.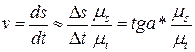 , (2.14)
, (2.14)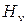 отметим точку
отметим точку 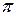 , именуемую полюсом. Из полюса проводим лучи, параллельные хордам, которые на оси ординат отсекут отрезки 01'; 021 и т. д. Полученные отрезки пропорциональны тангенсам соответствующих углов а, для пятого участка, например,
, именуемую полюсом. Из полюса проводим лучи, параллельные хордам, которые на оси ординат отсекут отрезки 01'; 021 и т. д. Полученные отрезки пропорциональны тангенсам соответствующих углов а, для пятого участка, например, 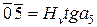 . Он представляет собой среднюю скорость движения ведомого звена в пределах рассматриваемого участка в масштабе
. Он представляет собой среднюю скорость движения ведомого звена в пределах рассматриваемого участка в масштабе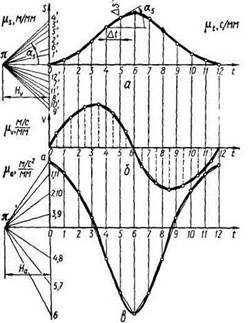
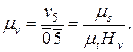 (2.15)
(2.15)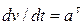 . Для случая прямолинейного движения тангенциальная составляющая равна полному ускорению.
. Для случая прямолинейного движения тангенциальная составляющая равна полному ускорению. (2.16)
(2.16)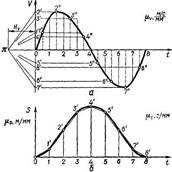 ки на оси ординат (например /', 2' и т. д.) лучами соединяются с полюсом
ки на оси ординат (например /', 2' и т. д.) лучами соединяются с полюсом 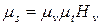 .
.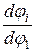 , получившую название аналога угловой скорости. Связь между аналогом скорости и действительной угловой скоростью i -ro звена определится из соотношения
, получившую название аналога угловой скорости. Связь между аналогом скорости и действительной угловой скоростью i -ro звена определится из соотношения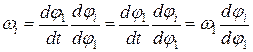 , т. е. угловая скорость i -го звена
, т. е. угловая скорость i -го звена  равна произведению угловой скорости ведущего звена
равна произведению угловой скорости ведущего звена  на аналог скорости. Продифференцировав уравнения (2.3) и подставив значение аналога скорости, получаем уравнения для определения угловой скорости шатуна
на аналог скорости. Продифференцировав уравнения (2.3) и подставив значение аналога скорости, получаем уравнения для определения угловой скорости шатуна 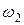 (рис. 2.2) и относительной скорости звена 3 —
(рис. 2.2) и относительной скорости звена 3 — 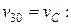
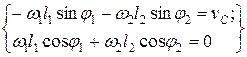 (2.17)
(2.17)
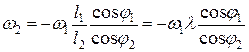
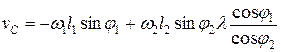 =
= 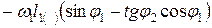 . (2.18)
. (2.18)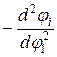 , можно определить действительное ускорение i -ro звена, умножив аналог углового ускорения на квадрат угловой скорости ведущего звена
, можно определить действительное ускорение i -ro звена, умножив аналог углового ускорения на квадрат угловой скорости ведущего звена 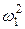 . При этом принимая, что
. При этом принимая, что 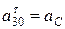 :
: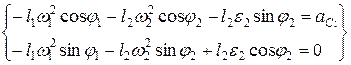 (2.19)
(2.19)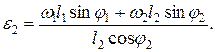
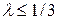 , пользуются приближенными формулами при определении перемещения, скорости и ускорения ползуна. При этом перемещение ползуна Sс измеряем от мертвого положения Со (рис. 2.2): Sc =
, пользуются приближенными формулами при определении перемещения, скорости и ускорения ползуна. При этом перемещение ползуна Sс измеряем от мертвого положения Со (рис. 2.2): Sc = 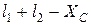 , или с учетом (2.5) получим
, или с учетом (2.5) получим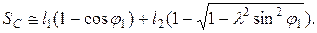 (2.20)
(2.20)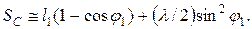 ( 2.21 )
( 2.21 )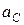 определяют по формулам:
определяют по формулам: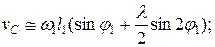 (2.22)
(2.22) (2.24)
(2.24)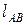 = 0,1 м; lCD = 0,3 м; lАС = 0,125 м при
= 0,1 м; lCD = 0,3 м; lАС = 0,125 м при 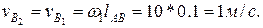
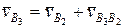 ;
; 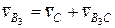 .. D4
.. D4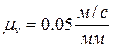 . Скорость
. Скорость 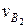 откладываем от полюса
откладываем от полюса 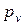 (рис.2.6, б) в виде отрезка pvb2 = 1/0,05 = 20 мм, перпендикулярного к кривошипу 1. Скорость vс = 0 определяется точкой, совпадающей с полюсом рv. Через точки b2 и с проводим соответственно линии действия скоростей
(рис.2.6, б) в виде отрезка pvb2 = 1/0,05 = 20 мм, перпендикулярного к кривошипу 1. Скорость vс = 0 определяется точкой, совпадающей с полюсом рv. Через точки b2 и с проводим соответственно линии действия скоростей 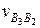 — параллельно звену 3 (кулисе) и
— параллельно звену 3 (кулисе) и 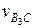 — перпендикулярно к кулисе. Пересечение линий действия скоростей
— перпендикулярно к кулисе. Пересечение линий действия скоростей  и относительных
и относительных 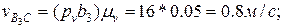
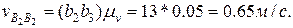
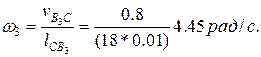
 Определяем скорости звеньев группы пятого вида. Аналогично предыдущему выбираем на звене точку D5, совпадающую с центром вращательной пары D4. Скорость точки D5 определим через известные скорости точек звеньев, примыкающих к звену 5: точки D4 на звене 4 и Do на звене 0.
Определяем скорости звеньев группы пятого вида. Аналогично предыдущему выбираем на звене точку D5, совпадающую с центром вращательной пары D4. Скорость точки D5 определим через известные скорости точек звеньев, примыкающих к звену 5: точки D4 на звене 4 и Do на звене 0.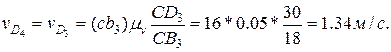
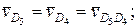

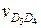 параллельно направляющей поступательной пары 4 — 5 и
параллельно направляющей поступательной пары 4 — 5 и 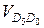 — параллельно направляющей поступательной пары 5 — 6 до их пересечения в точке D5. Абсолютная скорость точки D5
— параллельно направляющей поступательной пары 5 — 6 до их пересечения в точке D5. Абсолютная скорость точки D5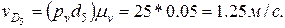
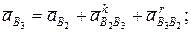
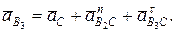
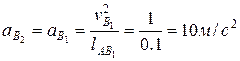 /
/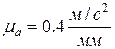 параллельно кривошипу 1 в направлении от точки В1 до А (рис. 2.6, b) в виде отрезка
параллельно кривошипу 1 в направлении от точки В1 до А (рис. 2.6, b) в виде отрезка  . Ускорение точки С ac = 0, следовательно, точка с б удет находиться в полюсе плана ускорений рa.
. Ускорение точки С ac = 0, следовательно, точка с б удет находиться в полюсе плана ускорений рa.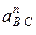 и кориолисова
и кориолисова  определим по формулам, аналогичным формулам (2.11) и (2.12), пользуясь планом скоростей (рис. 2.6, б):
определим по формулам, аналогичным формулам (2.11) и (2.12), пользуясь планом скоростей (рис. 2.6, б):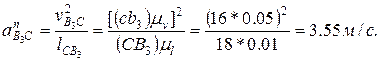
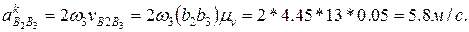
 и
и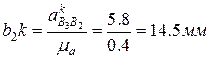 откладываем на плане ускорений: первый от точки с параллельно звену 3 в направлении от точки В3 к точке С; направление второго отрезка определится поворотом вектора относительной скорости
откладываем на плане ускорений: первый от точки с параллельно звену 3 в направлении от точки В3 к точке С; направление второго отрезка определится поворотом вектора относительной скорости 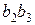 вокруг своего начала (точки b2) в сторону направления вращения кулисы 3 (среды переноса). Через точки п и k проводим перпендикулярно к отрезкам сп и b2k линии действия ускорения
вокруг своего начала (точки b2) в сторону направления вращения кулисы 3 (среды переноса). Через точки п и k проводим перпендикулярно к отрезкам сп и b2k линии действия ускорения 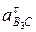 и
и 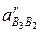 .Пересечение этих линий даст точку b3, определяющую конец вектора ускорения точки
.Пересечение этих линий даст точку b3, определяющую конец вектора ускорения точки 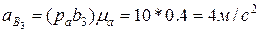 .
.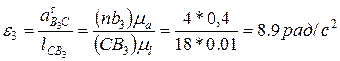 . Направление его можно установить, как указано ранее.
. Направление его можно установить, как указано ранее.
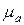 откладываем его в виде отрезка
откладываем его в виде отрезка 
 точки D5 составим векторные уравнения:
точки D5 составим векторные уравнения: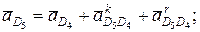

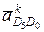 и
и 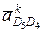 равны нулю вследствие того, что угловые скорости среды переноса w5 и w0 равны нулю. Поэтому через точки d4 и d0 (находящиеся в полюсе ра) проводим линии действия относительных ускорений
равны нулю вследствие того, что угловые скорости среды переноса w5 и w0 равны нулю. Поэтому через точки d4 и d0 (находящиеся в полюсе ра) проводим линии действия относительных ускорений 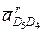 и
и  параллельно направляющим поступательных пар, образованных звеньями 4 — 5 и 5 — 0 соответственно.
параллельно направляющим поступательных пар, образованных звеньями 4 — 5 и 5 — 0 соответственно.