Связность и симплициальные комплексы

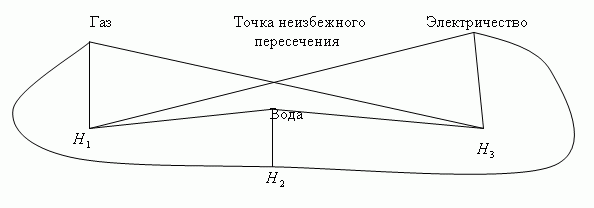
Приближенно симплициальный комплекс состоит из множества вершин X и множества симплексов Y, образованных из этих вершин в соответствии с заданным бинарным отношением.Симплициальный комплекс образован множеством симплексов Y, связанных через общие грани, т.е. через общие вершины. Например, можно положить Y = X = {птицы, лисы, насекомые, травы, антилопы}. При этом отношение таково: симплекс состоит из всех вершин, таких, что X_j является жертвой Y_i. Таким образом, Y_i = «птицы» — 1-симплекс, состоящий из вершин «насекомые» и «травы», y₂ = «лисы» — 1-симплекс, состоящий из вершин «птицы» и «насекомые» и т.д. Отметим, что n-симплекс состоит из n+1 вершин и его размер на единицу меньше числа вершин.

Вообще говоря, p — симплекс представляется выпуклым многогранником с вершинами в эвклидовом пространстве, а комплекс K_y(X,L) совокупностью таких многогранников в эвклидовом пространстве E. Хотя размерность наверняка не превышает суммы размерностей всех симплексов из K_y(X,L), однако поскольку многие симплексы имеют общие грани, то размерность на самом деле окажется меньше. В действительности можно показать, что если dim[K_y(X,L)] = n, то 7 a 1 = 2⋅n + 1. Так, если dim[K_y(X,L)] = 1, то наибольший порядок есть p = 1, поэтому можно ожидать, что трехмерного пространства E₃ будет достаточно, чтобы геометрически представить произвольный комплекс размерности 1. Это можно проиллюстрировать следующим образом: на плоскости (E₂) надо соединить непересекающимися линиями три дома H₁, H₂ и H₃ с источником газа, воды и электроэнергии. Неразрешимость поставленной задачи иллюстрирует наше утверждение. Задача графически изображена на рис.7.5, а ее решение в E₃ показано на рис.7.6.

Рис.7.5 — Проблема пересечений в E₂

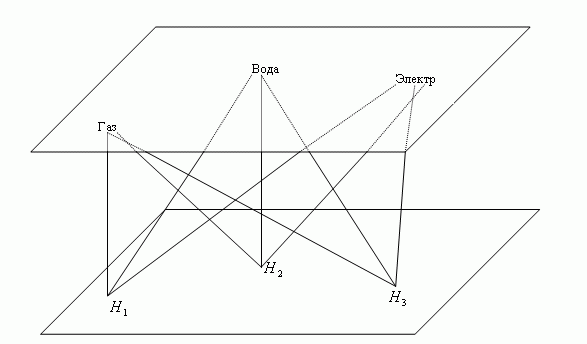
Рис.7.6 — Решение проблемы пересечений в E₂

Основываясь на геометрической интуиции, можно изучать многомерную связную структуру комплекса K_y(X,L) различными способами с привлечением алгебраических методов. В связи с этим рассмотрим некоторые важные понятия.

Q — связность

Это понятие связано с изучением цепочек связи, таких, что каждый симплекс в цепи имеет общую вершину с соседними симплексами, q = 0, 1, 2,..., dim[К-1]. Геометрически эти цепи содержат достаточно много локальной информации относительно того, каким образом симплексы, составляющие комплекс, связаны друг с другом. Если представить себе,что мы можем «видеть» только в пространстве размерности 7. 0 q (скажем с помощью специальных очков), то, рассматривая комплекс K_y(X,L) мы увидим, что он распадается на несколько несвязанных элементов. Подобное геометрическое представление порождает алгебраическую теорию q-связности, позволяющую гораздо лучше понять процессы обмена информацией внутри комплекса.

Эксцентриситет

Для того, чтобы понять каким образом отдельные симплексы «вложены» в комплекс, вводится понятие эксцентриситета. Это понятие отражает как относительную важность данного симплекса для комплекса в целом (через его размерность), так и его значимость как связующего звена (через максимальное число его вершин, принадлежащих также любому другому симплексу). Другими словами, эксцентриситет позволяет увидеть и оценить, насколько «плотно» каждый симплекс вложен в комплекс.

Образ

Как мы уже отмечали в предыдущих лекциях для описания динамики системы необходимо ввести отображение каждого симплекса из K_y(X,L) П: G_i->k i = 0, 1... dim[K] r = 1, 2... card[K] в соответствующее числовое поле: Образ П отражает динамические изменения, происходящие в комплексе со временем. Поскольку каждый симплекс 7 s 4i 0 обладает характеристической геометрической размерностью, то же справедливо и для связанных с ним численных величин. Следует иметь в виду, что геометрическая структура налагает различные ограничения на изменение образа, т.е. на динамику системы.

Гомотопия

Вопрос о том, насколько «близким» является данный симплекс (цепь) к другому симплексу (цепи), представляет как теоретический, так и прикладной интерес. Если ввести понятие 1 гомотопия 0, то можно получить ответ не только на этот вопрос, но и на вопрос о том, можно ли непрерывным преобразованием трансформировать одну цепь в другую, не нарушая геометрии системы. Так, например, кривые А и A^* на торе (см.рис.2.9) являются гомотопными, а кривые В и B^* нет, поскольку наличие «дырки» в центре не позволяет непрерывно деформировать В в B^*. Аналогичные понятия могут быть введены и для комплекса и не исключено, что они могут быть полезными при анализе его структуры. Хотя с чисто математической точки зрения изложенные геометрические понятия совершенно элементарны, они все же дают весьма подробную информацию, необходимую для понимания статической геометрии данного бинарного отношения и возможной динамики соответствующей ему связной структуры.

Рис.7.7 — Гомотопия на торе