
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функциональная схема вычислительного устройстваСодержание книги
Поиск на нашем сайте
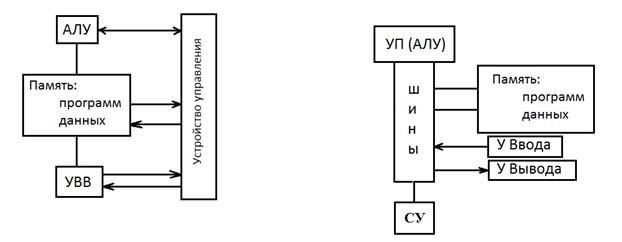
Для упрощения процесса программирования в 1945 году был создан первый компьютер с устройством хранения информации – оперативной памятью. К работе был привлечён Джон Фон Нейман, сформулировавший принципы построения вычислительных устройств, согласно которым для работы необходимы: 1) арифметико-логическое устройство (процессор); 2) память (программ и данных); 3) устройство для ввода/вывода информации. На рисунке изображена схема построения ВЧТ. АЛУ – арифметико-логическое устройство; П – память (ПП - память программ, ПД – память данных); УВВ – устройство ввода-вывода; Ш - шины (шины адресов, шины данных); СУ - система управления.
Шина представляет собой набор из n (число разряда проводов), объединенных по функциональному назначению. По шине данных передаются только данные. На шине адреса устанавливаются только номер ячейки памяти либо порта, с которым производится обмен данными. По шине управления передаются служебные сигналы, сопрягающие процессы обмена данными и прочие процессы (запросы прерываний, работа схем прямого доступа к памяти и т.д.).
Формы представления данных в вычислительных системах Шина данных – параллельное определённое включение проводов. Каждый из проводов может быть в одном из 2-х состояний. Каждый разряд имеет свой вес, или показатель степени (2n), n – номер разряда.
deс – обозначение десятичного кода; hex – обозначение шестнадцатеричного кода. Двоичная система Двоичный код – активное значение в одном разряде может принимать только 2 значения: «0» или «1». Максимальное число, которое может быть записано с помощью 1 байта = 256 Системы исчисления Система исчисления — символический метод записи чисел, представление чисел с помощью письменных знаков. Системы исчисления подразделяются на позиционные, непозиционные и смешанные. В вычислительной технике нашли применение позиционные системы исчисления. Позиционная система исчисления - система исчисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда). Позиционная система счисления определяется целым числом D>1, называемым основанием системы счисления. Система счисления с основанием D также называется
В вычислительных устройствах для записи заданных значений применяют двоично-десятичное кодирование десятичных цифр (Binary-Coded Decimal), при этом для одной двоично-десятичной цифры отводится четыре двоичных разряда (двоичная тетрада). Также используется шестнадцатеричная система исчислений, в которой для записи одного значения аналогично используют 4 разряда. Если суммарное значение превышает 9, то используются буквы латинского алфавита A-F. При объединении 4-х разрядов в один знак получим младший и старший разряд. dec → bin, hex При переводе числа из десятичной системы счисления в произвольную применяется метод последовательного деления deс-числа на основание произвольной системы. Остаток от деления записывается как младший бит, а частное (если оно не равно 0) вновь подвергается делению на основание произвольной системы. Каждый следующий остаток записывается в разряд нового числа в направлении от младшего разряда к старшему. dec ← bin, hex Для перевода числа в десятичную систему счисления из произвольной необходимо представить его в виде суммы произведений степеней основания произвольной системы счисления на соответствующие цифры в разрядах числа произвольной системы. bin → hex Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой из вышеприведённой таблицы перевода. Таблица и правила перевода чисел из одной системы исчисления в другую
Dec |
Hex | ||||||||
| 8 | 4 | 2 | 1 | |||||||
| 8 | 4 | 2 | 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 1 | 1 | 1 | |||||
| 0 | 0 | 1 | 0 | 2 | 2 | |||||
| 0 | 0 | 1 | 1 | 3 | 3 | |||||
| 0 | 1 | 0 | 0 | 4 | 4 | |||||
| 0 | 1 | 0 | 1 | 5 | 5 | |||||
| 0 | 1 | 1 | 0 | 6 | 6 | |||||
| 0 | 1 | 1 | 1 | 7 | 7 | |||||
| 1 | 0 | 0 | 0 | 8 | 8 | |||||
| 1 | 0 | 0 | 1 | 9 | 9 | |||||
| 1 | 0 | 1 | 0 | 10 | A | |||||
| 1 | 0 | 1 | 1 | 11 | B | |||||
| 1 | 1 | 0 | 0 | 12 | C | |||||
| 1 | 1 | 0 | 1 | 13 | D | |||||
| 1 | 1 | 1 | 0 | 14 | E | |||||
| 1 | 1 | 1 | 1 | 15 | F |
Общий принцип:
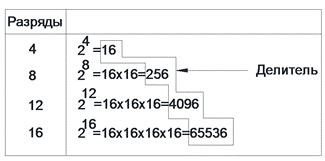
1. Берется число хххх делится на подходящий делитель, так, чтобы был не нулевой результат;
2. Результат умножается на делитель;
3. Из хххх вычитается результат операции 2;
4. С остатком выполняются аналогичные операции с 1 по 4;
5. Последний остаток (<16) в младшие разряды.
bin ← hex
|
|
Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из вышеприведённой таблицы перевода.
Пример:
Запишем 100deс:
|
Dec
| D 7 | D 6 | D 5 | D 4 | D 3 | D 2 | D 1 | 0 |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 | |
| → bin | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| → hex | 100/16= 6, остаток 4 | |||||||
Так, 100dec = 01100100bin = 64hex.
Запишем 55hex:
|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 | |
| → bin | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| → de с | 5 · 20 + 5 · 24 = 85 dec | |||||||
Так, 55hex = 01010101bin = 85dec.
Запишем 0A34hex:
|
| 2 15 | 2 14 | 2 13 | 2 12 | 2 11 | 2 10 | 2 9 | 2 8 | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 | |
| hex | 0 | A | 3 | 4 | ||||||||||||
| → bin | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| → de с | 0·212 + A·28 + 3·24 + 4·20 = 2612 dec | |||||||||||||||
Так, 0A34hex = 0000101000110100bin = 2612 dec.
- 1 разряд - это 1 бит информации;
- 8 разрядов = 1 байт;
- 8 разрядов и более составляют слово.
Допустим, есть переменная А.
Для хранения 1 байта она должна иметь символьный тип char:
char 55
0x55, // hex
0 1010101 b // bin
Если переменная имеет более 56 цифр, то она должна иметь целочисленный тип int или longint:
int // 0÷216 = 65535
longint // 0÷232 = 4294967296
Переменные вещественных чисел описываются типами float или double float (точность последнего в два раза больше первого и составляет 15 значащих цифр). Float позволяет хранить 4 байта информации, тогда как double float – 8 байт.
В большинстве случаев тип double float является наиболее удобным: ограниченной точности чисел float во многих случаях попросту недостаточно. Причина, по которой тип float все ещё используется, - экономия памяти при хранении, что важно при работе с большими массивами вещественных чисел.
|
| Поделиться: |

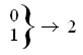 bin – обозначение двоичного кода;
bin – обозначение двоичного кода;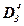
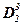
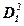
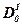
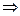 64hex
64hex


