
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
V. Знакомство с новым материаломСодержание книги
Поиск на нашем сайте
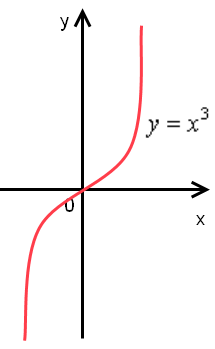
Рассказ учителя с показом презентации Учитель: Вы знакомы с функциями y = x, y = x2, y = x3и т.д. Все эти функции являются частным случаем степенной функции, т.е. функции y = xn, где х - независимая переменная, а n–натуральное число. Рассмотрим свойства степенной функции в частном порядке:
Учитель: Кто попробует вспомнить свойства этой функции:
VI. Физкультминутка
Здоровье - это не все, что надо человеку,но если его нет, то человеку уже ничего не надо. Поэтому мы сейчас вспомним о нашем здоровье и проведём физкультминутку. VII. Работа с учебником 1. № 138 (а, б) - устно а) f(3,7) < f(4,2) б) f(-5,2) > f(-6,5) 2. №139 (в, г) VIII. Подготовка к ГИА А сейчас мы с вами выполним задание из демоверсии ГИА
IX. Самостоятельная работа учащихся Выполнение тестового задания (Приложение) X. Домашнее задание П.8 № 140,141, по повторению №156 XI. Рефлексия Недаром говорится: лицо – зеркало души. Вот это мы сейчас и проверим. Меня интересует настроение, с которым вы заканчиваете урок. График какой функции похож на выражение ваших губ, отображающих настроение на уроке.
Студент _____________ ______________ подпись Ф.И.О Руководитель практикой ___________ __________ ______________ оценка подпись Ф.И.О Дата
План – конспект урока по геометрии в 9 классе по теме: «Теорема косинусов» Цель урока: Развитие у учащихся пространственного воображения и логического мышления путем изучения теоремы косинусов и применения этих знаний при решении задач вычислительного и конструктивного характера. Задачи урока: 1. Обучающая: отрабатывать применение данной теоремы при решении задач, совершенствовать навыки решения задач; 2. Развивающая: развитие познавательной активности, творческих способностей, мышления, умения анализировать и обобщать, переносить знания из одной ситуации в другую; 3. Воспитательная: воспитание чувства ответственности каждого учащегося, интереса к предмету с привлечением мультимедийных возможностей компьютера и элементов занимательности; 4. Методическая: показать применение методов дифференцированной работы при решении задач. Оборудование: мультимедийный проектор, презентация на тему «Теорема косинусов», набор карточек. Формы работы учащихся: фронтальная, индивидуальная, самостоятельная в режиме самоконтроля и взаимоконтроля. Тип урока: урок ознакомления с новым материалом Ход урока 1.Организационный момент. Проверка готовности рабочего места к уроку (приветствие, проверка готовности к уроку, рабочих тетрадей, письменных принадлежностей). 2.Актуализация опорных знаний. Сообщение темы, цели и задач урока. Мотивация учебной деятельности. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний Этап подготовки к восприятию нового материала. (Фронтальная работа с классом) 1. Повторение. (Ученица1 у доски). Рассказ о косинусе угла: определение;значения косинусов некоторых углов от от 0о до 90о свойство косинусов равных углов; свойство косинусов смежных углов; свойство косинусов углов, значения которых увеличиваются от 0о до 90о. (Ученица 2). Слайд 2
(Ученица 3) Используя четырехзначные математические таблицы Брадиса, найдите 1) cos25о; 2) угол
2.Изучение нового материала.(Использую слайды из презентации «Теорема косинусов».) Историческая справка: Впервые теорема косинусов была доказана учёным –математиком аль-Бируни (973-1048 г.г.). С помощью данной теоремы и теоремы синусов можно будет полностью решить задачу: «Решить треугольник», т.е. как зная одни из основных элементов треугольника (их 6: 3 угла и 3 стороны), найти другие. Слайд. Теорема. В каждом треугольнике квадрат любой стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Дано:
В)если – тупой. Слайд 6. Доказательство проведите самостоятельно. Работа с учебником 1. Прочитайте доказательство теоремы в учебнике стр.161. Основные задачи – следствия из теоремы косинусов 1. Нахождение третьей стороны треугольника. Слайд 7.
2. СЛЕДСТВИЕ 1. Нахождение углов треугольника. Слайд 8. Найдите наибольший угол треугольника, если известны все его стороны. Запишите соответствующие формулы – следствия из теоремы косинусов
3. СЛЕДСТВИЕ 2.Определение вида треугольника, зная его стороны (cлайд 9). Задание: определите вид треугольника с заданными сторонами, вычислив предварительно косинус наибольшего угла:
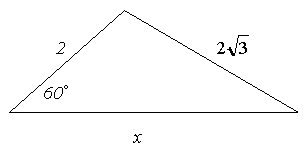
Как можно ответить на этот вопрос без вычисления косинуса наибольшего угла? ВЫВОД. Пусть с – наибольшая сторона 3. Закрепление материала. Решение задач Динамическая пауза(упражнение для глаз и мышц шеи) 1. Работа в парах. Задачи по готовым чертежам. Чертежи проектируются при помощи проектора. При решении задач учащиеся каждый раз проговаривают формулировку теоремы. Задача 1
Ответ: Задача 2
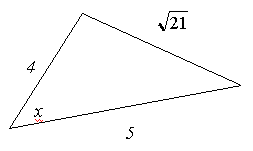
Ответ: 4. Задача 3
Ответ: 60°. 4.Проверка усвоенного материала проводится в форме тестирования. Проводится тест 1. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то эта сторона лежит против: а) тупого угла 2. В а) угла А 3. Треугольник со сторонами 5, 6 и 7 см: а) остроугольный 4. Если в а) АВ 5. Если квадрат стороны треугольника больше суммы квадратов двух других его сторон, то эта сторона лежит против: а) острого угла Самопроверка. Ответы:
5.Итоги урока Оценка работы учащихся. Дать анализ и оценку успешности достижения цели и наметить перспективу последующей работы. 7.Домашняя работа:выучить доказательство теоремы косинусов и решить задачи (выданы каждому – индивидуально) 8. Рефлексия Студент _____________ ______________ подпись Ф.И.О Руководитель практикой ________ _____________ ______________ оценка подпись Ф.И.О Дата
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 88; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.87.168 (0.006 с.) |



 Приложение.
Приложение. 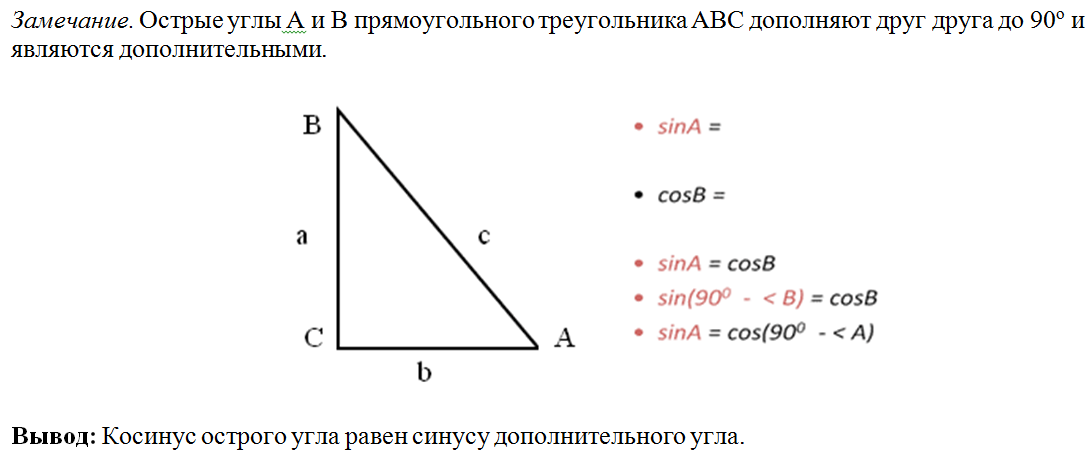
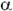 , если cos
, если cos 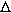 АВС АВ = с, АС = b, ВС = а
АВС АВ = с, АС = b, ВС = а 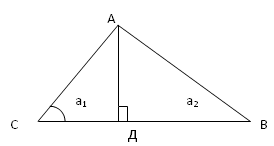 Пусть АД – высота, АД = h. Из
Пусть АД – высота, АД = h. Из 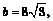 с = 7.
с = 7. 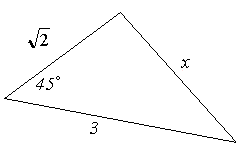
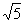 .
.
 АВС известны длины сторон АВ и ВС. Чтобы найти сторону АС, необходимо знать величину:
АВС известны длины сторон АВ и ВС. Чтобы найти сторону АС, необходимо знать величину: А=48°;
А=48°; 


