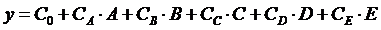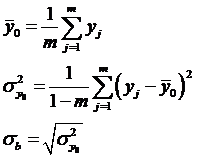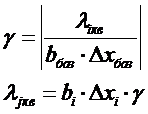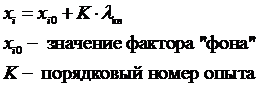Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейное приближение и коэффициенты регрессииСодержание книги
Поиск на нашем сайте
Выполнив 8 опытов и получив значение параметра оптимизации необходимо обработать результаты. Для этого следует вычислить коэффициенты регрессии для каждого фактора, используя формулу:
Иными словами, необходимо умножить значение уровня фактора в опыте на значение параметра в этом опыте и сложить получившиеся значения для каждого фактора. На выходе получатся коэффициенты регрессии, из которых составляется уравнение регрессии вида:
При составлении уравнения регрессии следует помнить, что значения коэффициентов не берутся по модулю, поэтому если коэффициент отрицательный, то и в уравнении будет соответственно вычитание. На основе уравнения регрессии можно сделать вывод о вкладе каждого фактора в значение выходного параметра. Чем больше модуль коэффициента, тем большее влияние соответствующий фактор оказывает на выходной параметр. Если перед коэффициентом стоит знак «+», то это означает, что с увеличением значения фактора параметр возрастает. В том случае, если перед коэффициентом стоит знак «-» - фактор оказывает негативное влияние на выходной параметр и снижение его значения увеличит конечный выход. Короче говоря, прямая и обратная зависимость. Оценка значимости коэффициентов регрессии Оценку ошибки эксперимента начинают с вычисления дисперсии воспроизводимости параметра оптимизации. Параллельно с экспериментами следует провести m опытов (3 – 4) в режиме «фона». Полученные данные следует обработать с помощью формул:
Коэффициенты регрессии считаются значимыми (при 5%-ом уровне значимости) если:
Значимость коэффициентов регрессии указывает на необходимость изменения значений факторов эксперимента. В том случае, если коэффициент незначимый – соответствующее ему значение фактора эксперимента не изменяется, так как не оказывает практически никакого эффекта на выходной параметр. Его значение принимаю фоновым и считают фиксированным. Этап движения по градиенту Для движения по градиенту необходимо изменять значения факторов Xi в соответствии с их коэффициентами регрессии. Для этого следует произвести следующие действия: 1. Для всех i-ых факторов вычислить произведение bi и Dxi. Фактор, у которого абсолютное значение этого произведения является максимальным, принимается как базовый; 2. Для базового фактора произвольно выбирается величина шага крутого восхождения liкв; 3. Вычислить шаги крутого восхождения для остальных факторов, коэффициенты регрессии которых значимы. Для этого следует воспользоваться формулами:
4. Все значения шагов крутого восхождения берутся с соответствующими им знаками коэффициентов регрессии. После определения шагов крутого восхождения для всех факторов планируют серию опытов, в которых факторы принимают значения:
Для простоты работы следует составить таблицу:
При выборе шага базового фактора следует учитывать, что в процессе исполнения опытов его значение должно выйти за пределы определения, прописанного в самом начале. Реализацию плана крутого восхождения следует начинать с тех опытов, условия которых выходят за область эксперимента (в этапе линейного приближения) хотя бы по одному из факторов. При движении по градиенту может встретиться случай, что до достижения оптимума один из варьируемых факторов окажется у границы своей области определения. Тогда такой фактор фиксируется в этой точке и в дальнейшем не варьируется. Определение оптимума Наилучшее значение параметра оптимизации нередко и является решением задачи. Однако чаще этапы линейного приближения и движения по градиенту необходимо повторять по несколько раз. После первого движения по градиенту в точке наилучшего значения параметра оптимизации вновь ставят линейное приближение, то есть принимают за «фон» нового эксперимента. По результатам этого эксперимента вновь выполняют крутое восхождение.
ВОПРОС №4. КУЛЬТИВИРОВАНИЕ КЛЕТОК И ТКАНЕЙ РАСТЕНИЙ, ЖИВОТНЫХ И ЧЕЛОВЕКА Методы клеточной биологии находят всё большее распространение в различных областях современных фундаментальных и прикладных исследований. Одним из наиболее используемых является метод культивирования клеток растений, животных и человека, получивший широкое распространение во второй половине XX века. В настоящее время можно культивировать клетки практически всех тканей и органов человека, животных и растений. Культивирование клетки становится основой современных наукоемких технологий в биотехнологии и медицине. Например, в биотехнологии - получение биологически активных веществ, вакцин, диагностикумов, клеток-продуцентов; в медицине – заместительная клеточная терапия, позволяющая восстанавливать поврежденные ткани путем трансплантации нормальных здоровых клеток человека, выращенных in vitro. Открытие принципа гибридомной техники привело к получению в 1975 году моноклональных антител из гибридомных клеток. В перспективе с помощью метода культивирования клеток и тканей животных может быть налажено производство мышечной и других тканей, которые планируется использовать в мясной промышленности вместо сырья, получаемого в результате убоя сельскохозяйственных животных. Клеточные культуры человека и животных делятся на первичные, то есть растущие ограниченное время и постоянные (трансформированные, перевиваемые) клеточные линии (культуры), растущие неограниченно долго. Для получения первичных культур удобнее всего использовать эмбриональные ткани – кожно-мышечную, почечную, легочную и другие после предварительной дезагрегации кусочков тканей с помощью фермента трипсин. Эмбриональные клетки обладают выраженной пролиферативной активностью вне организма и характеризуются стабильностью генома. Трансформированные клеточные линии (перевиваемые культуры) интенсивно используются для фундаментальных и прикладных исследований. Во многих учреждениях, где проводятся исследования с использованием культивируемых клеток, существуют коллекции стандартных эталонных клеточных линий, позволяющие проводить исследования и производить вакцины и другие биологически активные вещества, используя клеточный материал со строго охарактеризованными свойствами. Явным преимуществом трансформированных (перевиваемых) культур перед первичными является не только неограниченный срок культивирования; они свободны от вирусов и микроорганизмов. Перевиваемая культура, однако, не лишена недостатков. Трансформация клеток затрагивает кариотип и изменяет свойства клеток, причем не исключено приобретение клетками онкогенных свойств. Поэтому для производства вакцин всё же используют первичные культуры тканей.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.200.93 (0.007 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

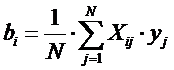 , где Xij – значение i-ого фактора в j-ом опыте (+1 или -1), yj – значение параметра оптимизации в j-ом опыте.
, где Xij – значение i-ого фактора в j-ом опыте (+1 или -1), yj – значение параметра оптимизации в j-ом опыте.