
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Учебный модуль Дифференциальное исчисление.Стр 1 из 3Следующая ⇒
Учебный модуль Дифференциальное исчисление. Тема Дифференциальное исчисление функции одной переменной ЛЕКЦИЯ 1. Определение производной. Правила дифференцирования. Пусть задана некоторая функция y = f (x). Выберем в области определения функции два произвольных значения аргумента х и х 1. Обозначим за Dх разность между двумя значениями аргумента D х = х 1 – х, (т.е х 1 = х +D х). Замечание. D х может быть как больше нуля, если х 1 > х, так именьше нуля, если х 1 < х. Вычислим значения функции в этих точках y = f (x) и y 1= f (x 1). Приращением функции D f (x) называется разность между двумя значениями функции D f (x) = f (x 1) - f (x) = y 1 – y или D f (x) = f (х + D x) – f (x). Если при D х ® 0 существует конечный предел отношения приращения функции к вызвавшему его приращению аргумента, то функция f (x) называется дифференцируемой в точке х, а значение предела называется производной от функции f (x) в точке х и обозначается
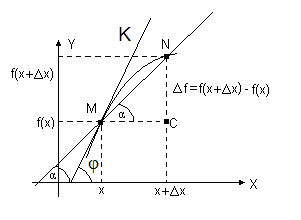
Производная – это функция от того же аргумента, что и f (x). Операция вычисления производной называется дифференцированием функции. Геометрический смысл производной. Если изобразить на рисунке график функции f (x), отметить точки х и х 1 = х + D х, то МС = D х, NC = D f (x). Величина отношения
равна тангенсу угла наклона секущей MN к оси абсцисс (см. рис.1.1). Если Dх ® 0, то точка N стремится по графику функции к точке M, секущая MN стремится занять положение касательной МК к графику функции f (x) в точке M, угол наклона секущей α стремится к углу наклона касательной φ. Сравнивая формулы (1.1) и (1.2) мы можем сказать, что значение производной f ¢(x) в точке х равно тангенсу угла наклона касательной к графику y = f (x) в точке М с координатами (х, f (x)). Уравнение касательной в точке М
уравнение нормали
Рис. 1.1. Геометрический смысл производной
В механике производная от пути по времени есть скорость Правила дифференцирования. На практике функции дифференцируют с помощью ряда правил и формул.
Производная постоянной С равна нулю (C)` = 0 (1.3) Производная линейной комбинации функций f 1 (x) и f 2(x) у (х) = с1f1 (x) +c2f2 (x), (1.4) где с1 и c2 произвольные постоянные, равна линейной комбинации производных у ¢(x) = (с1f1 (x) +c2f2 (x)) ¢ = с1f1 ¢ (x) +c2f2 ¢ (x). (1.5) Следствие. Постоянный множитель С можно вынести за знак производной (С у (x)) ¢= С у ¢(x). Производная произведения функций у (x) = f (x) у (x)’ = (f (x)g(x))¢ = f ¢(x)·ּ g (x) + f (x)·ּg ¢(x). (1.6) Правило можно обобщить на случай производной произведения n функций (f 1(x) = f 1(x)¢ Производная частного двух функций у (x) = f (x)/ g (x) вычисляется по правилу
(1.7)
Таблица производных основных элементарных функций
Примеры. 1. (6 sin x - 2 ln x)¢ = (6 sin x)¢ - (2 ln x)¢ = 6 (sin x)¢ - 2 (ln x)¢ = 6 cos x - 2. (lnx∙cosx)' =
3.
Правила дифференцирования
Дифференцирование сложной функции. Пусть дифференцируемая функция g (x) является аргументами другой функции f (x). В этом случае говорят о сложной функции у (x) = f (g (x)) или суперпозиции функций f и g. Вычислим производную сложной функции. Найдем приращение функции D у (x). Для этого выберем в области определения функции два произвольных значения аргумента х и х 1 = x + D x. Вычислим соответствующие значения функции g (x + D x) и g (x) и найдем ее приращение D g (x) = g (x + D x) - g (x) Аналогично найдем значения функции f (g (x + D x)) и f (g (x)). Тогда
D f = f (g (x +D x)) – f (g (x)) = f (g (x) + D g (x)) – f (g (x)). (1.8)
Подставим выражение (1.8) в (1.1). Умножим и разделим на D g (x) и сгруппируем сомножители. Тогда производная сложной функции
В компактной форме производную от сложной функции можно записать так
Иначе, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Пример. у = ln (sin (x 2)). Эта сложная функция состоит из следующих отдельных функций: f = ln g, g = sin h, h = x 2. При этом
Тогда Пример. Пользуясь формулами дифференцирования, найти производные следующих функций:
Решение. 1.
2. Производная сложной функции имеет вид
Теорема Ролля Пусть функция у = f (x): 1. непрерывна на отрезке [a, b], 2. дифференцируема во всех внутренних точках отрезка, т. е. в интервале (a,b), 3. f (а) = f (b). Тогда внутри отрезка (a, b) существует по крайней мере одна точка Замечание. Точка с является корнем производной. Если f(а) = f(b) =0, то теорема формулируется так: между корнями функции лежит корень производной.
Формула Лагранжа (формула конечных приращений). Пусть функция у = f (x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках отрезка, т. е. в интервале (a,b), то внутри отрезка существует по крайней мере одна точка с a < c < b в которой справедливо равенство: полное приращение функции равно производной, вычисленной в точке с, умноженной на длину промежутка f (b) - f (а) = f `(c)(b - а). (7.18)
В точке с касательная параллельна секущей MN (см. рис. 7.4).
Рис. 2.1. Геометрический смысл формулы конечных приращений.
Правило Лопиталя. Пусть функции f (x) и g (x) на отрезке [a,b] удовлетворяют условию теоремы Коши и f (с) = g (с) = 0 (a < c < b), то, если существует предел отношения производных при х →с, то существует и предел отношения функций в этой точке, причем
Замечание. Правило Лопиталя можно применять и для раскрытия неопределенностей типа Коротко полученную формулу читают так: предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует.
Если производные
Пример. Вычислить предел Решение. Так как е-х = 1/ех, то предел можно преобразовать к виду
ЛЕКЦИЯ 3. Приложение производных к исследованию функций. Использование производных позволяет прояснить многие особенности в поведении функций. Наиболее важными особенностями функций являются интервалы монотонности и точки экстремумов функций. Если функция относится к классу дифференцируемых монотонных функций, то ее производная сохраняет знак на интервале монотонности, причем возрастающая функция имеет положительную производную, а убывающая – отрицательную. Действительно, если Δх > 0, то так как
то знак производной совпадает со знаком приращения функции. Для возрастающих функций
Δf(x) > 0
для убывающих функций
Δf(x) < 0 Необходимые условия возрастания и убывания функций: если дифференцируемая на интервале Достаточные условия: если функция Функция имеет локальный максимум (минимум) в точке х 0, если она определена как в точке х 0, так и в окрестности этой точки, и значение функции в точке х 0 больше (меньше), чем ее значения во всех соседних точках: т. е.
f (х 0) > f (x) в точках максимума
f (х 0) < f (x) в точках минимума
для всех х из окрестности точки х 0.
Минимумы и максимумы функции объединены единым понятием – экстремумы. До точки максимума функция возрастает, следовательно, ее производная положительна
f `(x) > 0
после точки максимума – убывает, производная отрицательна
f `(x) < 0.
Для точки минимума первоначально функция убывает
f `(x) < 0,
а потом возрастает
f `(x)>0).
В самих точках экстремумов производная или равна нулю (обычный экстремум) или не существует (острый экстремум). На рис. 3.1 функция имеет экстремумы в точках х1, х2 и х3, причем в точке х1 – острый максимум, а в точках х2 и х3 обычный минимум и максимум. Тем самым, в точках экстремумов функции производная равна нулю или не существует (необходимое условие экстремума) и меняет знак с «+» на «-» в точках максимумов и с «-» на «+» в точках минимумов (достаточные условия экстремума).
Рис. 3.1. Экстремумы функции Точки, в которых производная равна нулю, называются стационарными точками. Не все стационарные точки являются точками экстремумов. В стационарных точках надо проверять достаточное условие экстремума. Замечание. Не надо путать наибольшее и наименьшее значение и экстремумы. Экстремум достигается всегда внутри промежутка, а наибольшее и наименьшее значения могут достигаться и в точках экстремумов, и на границах промежутка, и в точках разрыва. На рис. 3.1 точка х3 является точкой максимума и в ней также достигается наибольшее значение, наименьшее значение достигается в точке а, т.е. на границе промежутка.
Функция называется выпуклой (выпуклость вверх) на интервале (a,b), если график функции лежит под любой касательной в каждой точке интервала, на всем интервале выпуклости вторая производная отрицательна f ``(x) < 0. Функция называется вогнутой (выпуклость вниз) на интервале (a,b), если график функции лежит над любой касательной в каждой точке интервала, на всем интервале вогнутости вторая производная положительна f ``(x) > 0. Следовательно, в точках экстремумов вторая производная имеет определенный знак (достаточное условие экстремума по второй производной): в точках максимумов f ``(x 0) < 0, в точках минимумов f ``(x0) > 0. Достаточное условие существования точек перегиба. Если вторая производная
Рис. 3.2. Выпуклость и вогнутость кривой. Точка перегиба. Пример: y = x 2 e- x y `= 0 если x = 0 или x = 2, это стационарные точки. y ``= (2 x e- x – x 2e- x ))’ = 2e-x - 2 x e-x – 2 x e-x + x 2 e-x = e-x(2 - 4 x + x 2); y``= 0 если x1,2 =2 это точки перегиба y``(0) = 2 > 0, следовательно, в точке х = 0 минимум, y``(2) = -2e-2 < 0, следовательно в точке х = 2 максимум.
Асимптоты графика функции. Построение графика функции значительно облегчается, если знать его асимптоты. Понятие асимптоты рассматривалось при изучении формы гиперболы (в теме «кривые второго порядка»). Определение: асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис. 3.3).
Асимптоты могут быть вертикальными, наклонными и горизонтальными. Горизонтальная асимптота – это частный случай наклонной асимптоты. Прямая Действительно, в этом случае непосредственно из рисунка 3.3 видно, что расстояние точки
Прямая y = kx + b называется наклонной асимптотой для функции f (x), если при х→∞ расстояние от переменной точки графика функции М до прямой стремится к нулю (рис. 3.4). При этом
Рис. 3.4. Наклонная асимптота Если хотя бы один из пределов k и b не существует или равен бесконечности, то кривая В частности, если Замечание: Асимптоты графика функции Пример. y = x e-x.
Прямая у = 0 является горизонтальной асимптотой. Учебный модуль Дифференциальное исчисление.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.153.69 (0.095 с.) |
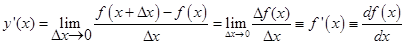
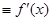 (1.1)
(1.1)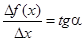 (1.2)
(1.2)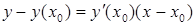 ,
,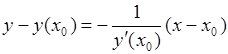 ,
,
 . Если функция
. Если функция  описывает какой-либо физический процесс, то производная y ’ есть скорость протекания этого процесса. В этом состоит физический смысл производной.
описывает какой-либо физический процесс, то производная y ’ есть скорость протекания этого процесса. В этом состоит физический смысл производной. g (x) вычисляется по правилу: произведение производной от первой функции на неизменную вторую плюс произведение производной от второй функции на неизменную первую
g (x) вычисляется по правилу: произведение производной от первой функции на неизменную вторую плюс произведение производной от второй функции на неизменную первую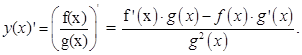
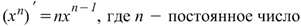 Производная степенной функции
Производная степенной функции
 Производная степенной функции
Производная степенной функции
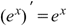 Производная экспоненциальной функции
Производная экспоненциальной функции
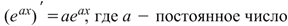 Производная экспоненты
Производная экспоненты
 Производная сложной экспоненциальной функции
Производная сложной экспоненциальной функции
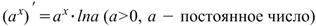 Производная экспоненциальной функции
Производная экспоненциальной функции
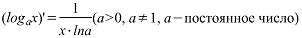 Производная логарифмической функции
Производная логарифмической функции
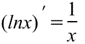 Производная натурального логарифма
Производная натурального логарифма
 Производная натурального логарифма функции
Производная натурального логарифма функции
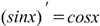 Производная синуса
Производная синуса
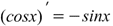 Производная косинуса
Производная косинуса
 Производная арксинуса
Производная арксинуса
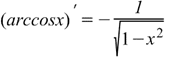 Производная арккосинуса
Производная арккосинуса
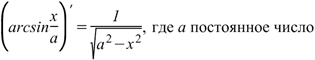 Производная арксинуса
Производная арксинуса
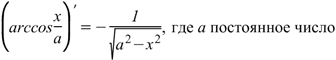 Производная арккосинуса
Производная арккосинуса
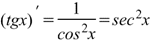 Производная тангенса
Производная тангенса
 Производная котангенса
Производная котангенса
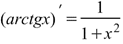 Производная арктангенса
Производная арктангенса
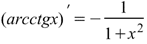 Производная арккотангенса
Производная арккотангенса
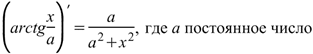 Производная арктангенса
Производная арктангенса
 Производная арккотангенса
Производная арккотангенса

 ∙cosx - lnx∙sinx
∙cosx - lnx∙sinx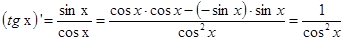
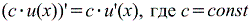
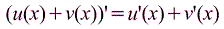


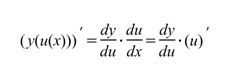
 g (x + D x) = g (x) + D g (x).
g (x + D x) = g (x) + D g (x). (1.9)
(1.9) (1.10)
(1.10)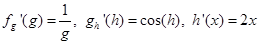
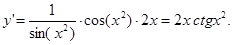
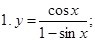

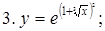

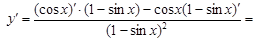
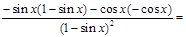
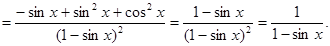
 есть сложная функция
есть сложная функция 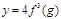 , где
, где 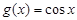 .
.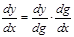 . Следовательно,
. Следовательно, .
.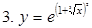 - сложная функция
- сложная функция 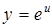 , где
, где 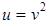 , а
, а  ,
, .
.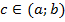 , в которой производная обращается в ноль – f `(c) = 0.
, в которой производная обращается в ноль – f `(c) = 0.



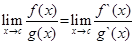 (2.1)
(2.1) .
.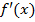 и
и 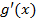 удовлетворяют тем же условиям, что и функции
удовлетворяют тем же условиям, что и функции 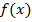 и
и 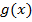 , теорему (2.1) можно применить ещё раз:
, теорему (2.1) можно применить ещё раз: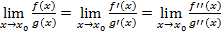 . (2.2)
. (2.2)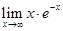 .
.
 .
.



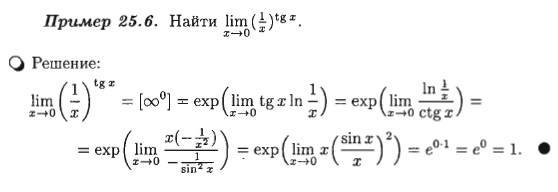
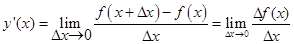
 f `(x) > 0,
f `(x) > 0, функция
функция  возрастает (убывает), то
возрастает (убывает), то  .
.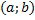 и
и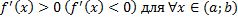 , то эта функция возрастает (убывает) на интервале
, то эта функция возрастает (убывает) на интервале 
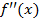 при переходе через точку
при переходе через точку 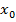 , в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой
, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой 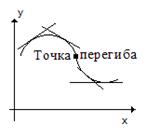
 y `= 2 x e- x - x 2 e- x = x e- x (2 – x);
y `= 2 x e- x - x 2 e- x = x e- x (2 – x); ,
,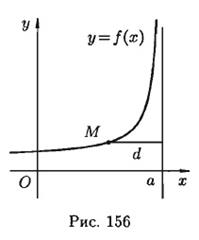 Рис. 3.3.
Рис. 3.3.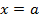 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции 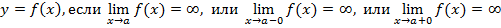 .
.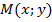 кривой от прямой
кривой от прямой 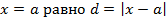 . Если
. Если 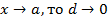 . Согласно определению асимптоты, прямая
. Согласно определению асимптоты, прямая 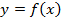 . Для отыскания вертикальных асимптот нужно найти те значения x, вблизи которых функция
. Для отыскания вертикальных асимптот нужно найти те значения x, вблизи которых функция 

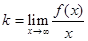 ,
, 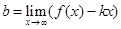 .
.
 . Поэтому
. Поэтому 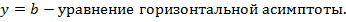
 могут быть разными. Поэтому при нахождении пределов k и b следует отдельно рассматривать случай, когда
могут быть разными. Поэтому при нахождении пределов k и b следует отдельно рассматривать случай, когда 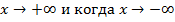 .
.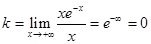 ,
,  .
.


