Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка гармонической функции. Гармонический анализ.Содержание книги Поиск на нашем сайте
Вопросы. 1.Приведите примеры физиологических кривых, полученных в результате исследований человека, которые можно при определенных условиях обрабатывать с помощью 1,2,3 и опишите, что это за условия. 2. Написать основные характеристики а). случайных величин; б). случайной функции; с). случайного процесса.
Методы первой категории - Эмпирическое распознавание Человеческий мозг справляется с задачей обнаружения микроорганизмов на изображениях более чем успешно. Попробуем использовать принципы, которыми руководствуется мозг при решении задачи распознавания. Попытку можно разделить на два метода или направления: методы распознавания "сверху-вниз" основанные на знаниях и методы распознавания "снизу-вверх" основанные на особенностях. Распознавание "сверху-вниз" означает построение некоторого набора правил, которым должен отвечать фрагмент изображения, для того чтобы быть признанным микроорганизмом. Этот набор правил является попыткой формализовать эмпирические знания о том, как именно выглядит микроорганизм на изображениях и чем руководствуется человек при принятии решения микроорганизм он видит или нет. Довольно легко построить набор простых и очевидных свойств изображения микроорганизма. Опираясь на эти свойства, можно построить алгоритм проверяющий их наличие на фрагменте изображения. К этому же семейству методик можно также отнести распознавание с помощью шаблонов, заданных разработчиком. Обнаружение микроорганизмов с помощью шаблона заключается в проверке каждой из областей изображения на соответствие заданному шаблону. Распознавание "снизу-вверх" использует инвариантные свойства изображений микроорганизмов, опираясь на предположение, что раз человек может без усилий распознать микроорагнизм на изображении независимо от его ориентации, условий освещения и индивидуальных особенностей, то должны существовать некоторые признаки присутствия микроорганизмов на изображений, инвариантные относительно условий съемки. Алгоритм работы методов распознавания "снизу-вверх" может быть кратко описан следующим образом: 1 Обнаружение элементов и особенностей (features), которые характерны для изображения микроорганизма;
2 Анализ обнаруженных особенностей, вынесение решения о количестве и расположении микроорганизмов; Моделирование класса изображений микроорганизмов с помощью Метода Главных Компонент (Principal Components Analysis, PCA) Метод главных компонент [12] применяется для снижения размерности пространства признаков, не приводя к существенной потере информативности тренировочного набора объектов. Применение метода главных компонент к набору векторов линейного пространства Rn, позволяет перейти к такому базису пространства, что основная дисперсия набора будет направлена вдоль нескольких первых осей базиса, называемых главными осями (или главными компонентами). Таким образом, основная изменчивость векторов тренировочного набора представляется несколькими главными компонентами, и появляется возможность, отбросив оставшиеся (менее существенные), перейти к пространству существенно меньшей размерности. Натянутое на полученные таким образом главные оси подпространство размерности m << n является оптимальным среди всех пространств размерности m в том смысле, что наилучшим образом (с наименьшей ошибкой) описывает тренировочный набор изображений. В приложении к задаче обнаружения микроорганизмов, МГК обычно применяется следующим образом. После вычисления главных осей тренировочного набора изображений микроорганизмов, вектор признаков тестового изображения проецируется на подпространство, образованное главными осями. Вычисляются две величины: расстояние от проекции тестового вектора до среднего вектора тренировочного набора - Distance in Feature Space (DIFS), и расстояние от тестового вектора до его проекции в подпространство главных компонент - Distance From Feature Space (DFFS). Исходя из этих расстояний выносится решение о принадлежности тестового изображения классу изображений микроорганизмов [13]. Моделирование класса изображений «лиц» с помощью Факторного анализа (Factor Analysis, FA) Факторный анализ (ФА) [15], как и многие методы анализа многомерных данных, опирается на гипотезу о том, что наблюдаемые переменные являются косвенными проявления относительно небольшого числа неких скрытых факторов. ФА, таким образом, это совокупность моделей и методов ориентированных на выявление и анализ скрытых (латентных) зависимостей между наблюдаемыми переменными. В контексте задач распознавания, наблюдаемыми переменными обычно являются признаки объектов. Факторный анализ можно рассматривать как обобщение метода главных компонент.
Цель ФА в контексте задачи обнаружения микроорганизмов - получить модель изображения микроорганизмов (с обозримым числом параметров), с помощью, которой можно провести оценку близости тестового изображения к изображению микроорганизмов [16]. 1.2.3 Проблема сбора контпримеров для тренировки классификаторов Методы, использующие МГК и ФА требуют для тренировки классификатора только набора положительных случаев распознавания (изображений микроорганизмов), им не требуются контрпримеры (изображения без микроорганизмов). Методы описанные ниже нуждаются также и в контрпримерах, что поднимает еще одну проблему - как найти репрезентативный набор изображений "не микроорганизма" для успешной тренировки классификатора? В работе [17] предложено решение этой проблемы методом самонастройки - он заключается в постепенном формировании набора контпримеров, по результатам проводимых тестов. На первом шаге для тренировки классификатора используется небольшого тренировочного набора изображений-контрпримеров. Затем производится тестирование на некоторой случайной выборке из базы данных изображений. Все изображения, в ходе теста ошибочно распознанные, как микроорганизмы, добавляются в набор контпримеров и тренировка повторяется. Линейный Дискриминантный Анализ (Linear Discriminate Analysis, LDA) Линейный Дискриминантный Анализ [14], в отличие от МГК и ФА не ставит своей целью найти подпространство меньшей размерности, наилучшим образом описывающее набор тренировочных изображений. Его задача состоит в поиске проекции в пространство, в котором разница между классами объектов максимальна. Это требование формулируется как получение максимально компактных кластеров, соответствующих различным классам, удаленных на максимально возможное расстояние. С помощью ЛДА удается получить подпространство небольшой размерности, в котором кластеры изображений микроорганизмов и "не микроорганизмов" пересекаются минимально. Производить классификацию в таком пространстве значительно проще [ 16 ]. Литература [1] M. H. Yang, D. J. Kriegman, N. Ahuja, " Detecting faces in images: A survey," IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 24, no. 1, pp. 34-58, Jan. 2002. [2] E. Hjelmas and B.K. Low, " Face detection: A survey," Journal of Computer Vision and Image Understanding, vol. 83, pp. 236-274, 2001. [3] G. Yang and T. S. Huang, " Human Face Detection in Complex Background," Pattern Recognition, vol. 27, no. 1, pp. 53-63, 1994. [4] C. Kotropoulos and I. Pitas, " Rule-Based Face Detection in Frontal Views," Proc. Int'l Conf. Acoustics, Speech and Signal Processing, vol. 4, pp. 2537-2540, 1997. [5] T. Sakai, M. Nagao, and S. Fujibayashi, "Line Extraction and Pattern Detection in a Photograph," Pattern Recognition, vol. 1, pp. 233-248, 1969. [6] I. Craw, H. Ellis, and J. Lishman, "Automatic Extraction of Face Features," Pattern Recognition Letters, vol. 5, pp. 183-187, 1987. [7] V. Govindaraju, " Locating Human Faces in Photographs," Int'l J. Computer Vision, vol. 19, no. 2, pp. 129-146, 1996. [8] K. Sobottka and I. Pitas, " A novel method for automatic face segmentation, facial feature extraction and tracking," Signal Processing: Image Communication, Vol. 12, No. 3, pp. 263-281, June, 1998. [9] F. Smeraldi, O. Carmona, and J. Big.un, " Saccadic search with Gabor features applied to eye detection and real-time head tracking," Image Vision Comput. 18, pp. 323-329, 2000. [10] M. C. Burl and P. Perona, " Recognition of planar object classes," in IEEE Proc. of Int. Conf. on Computer Vision and Pattern Recognition, 6, 1996. [11] L. C. De Silva, K. Aizawa, and M. Hatori, " Detection and tracking of facial features by using a facial feature model and deformable circular template," IEICE Trans. Inform. Systems E78-D(9), pp. 1195-1207, 1995.
[12] " "Метод главных компонент," Цифровая библиотека лаборатории компьютерной графики и мультимедиа при факультете ВМиК МГУ, http://library.graphicon.ru/catalog/19. [13] B. Moghaddam and A. Pentland, " Probabilistic visual learning for object representation," IEEE Trans. Pattern Anal. Mach. Intell. 19(1), pp. 696-710, 1997. [14] "Линейный дискриминантный анализ," Цифровая библиотека лаборатории компьютерной графики и мультимедиа при факультете ВМиК МГУ, http://library.graphicon.ru/catalog/184. [15] "Факторный анализ," Цифровая библиотека лаборатории компьютерной графики и мультимедиа при факультете ВМиК МГУ, http://library.graphicon.ru/catalog/217. [16] M.-H. Yang, N. Ahuja, and D. Kriegman, " Face Detection Using Multimodal Density Models," Computer Vision and Image Understanding (CVIU), vol. 84, no. 2, pp. 264-284, 2001. [17] K.-K. Sung and T. Poggio, " Example-Based Learning for View- Based Human Face Detection," IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 20, no. 1, pp. 39-51, Jan. 1998. [18] "Метод опорных векторов," Цифровая библиотека лаборатории компьютерной графики и мультимедиа при факультете ВМиК МГУ, http://library.graphicon.ru/catalog/217. [19] K.-R. Muller, S. Mika, G. Ratsch, K. Tsuda, and B. Scholkopf. " An introduction to kernel-based learning algorithms," IEEE Transactions on Neural Networks, 12(2), pp. 181-201, 2001. [20] Jochen Maydt and Rainer Lienhart. " Face Detection with Support Vector Machines and a Very Large Set of Linear Features," IEEE ICME 2002, Lousanne, Switzerland, pp. xx-yy, Aug. 2002 [21] D. Roth, M.-H. Yang, and N. Ahuja, " A SNoW-based face detector," in Advances in Neural Information Processing Systems 12 (NIPS 12), MIT Press, Cambridge, MA, pp. 855-861, 2000. [22] D. Roth, " The SNoW Learning Architecture," Technical Report UIUCDCS-R-99-2102, UIUC Computer Science Department, 1999. [23] N. Littlestone, " Learning Quickly when Irrelevant Attributes Abound: A New Linear-Threshold Algorithm," Machine Learning, vol. 2, pp. 285-318, 1988. [24] . 3.P. Juell and R. Marsh, " A hierarchical neural network for human face detection," Pattern Recog. 29, pp. 781-787, 1996. [25] S.-H. Lin, S.-Y. Kung, and L.-J. Lin, " Face recognition/detection by probabilistic decision-based neural network," IEEE Trans. Neural Networks 8, pp. 114-132., 1997 [26] H. A. Rowley, S. Baluja, and T. Kanade, " Neural network-based face detection," IEEE Trans. Pattern Anal. Mach. Intell. 20, pp. 23-38., January 1998 [27] Л.Р. Рабинер, " Скрытые марковские модели и их применение в избранных приложениях при распознавании речи: Обзор," Труды ИИЭР, т. 77, Номер 2, февраль 1989. [28] S. Marchand-Maillet and B. Merialdo, " Pseudo two-dimensional hidden markov models for face detection in colour images," in Proceedings Second International Conference on Audio- and Video-based Biometric Person Authentication (AVBPA), 1999. [29] G.J.Edwards, C.J.Taylor, T.F.Cootes, " Interpreting Face Images using Active Appearance Models," Int. Conf. on Face and Gesture Recognition 1998. pp. 300-30, 1998.
Вопросы: 1.На какие две части возможные для реализации процесса распознавания можно разделить процесс распознавания образа в медицине? 2. Банки и классы признаков в системе распознавания образа. Связь и различия. 3. Требования, предъявляемые к базе знаний в системе распознавания образа биообъекта?
4.Почему так не просто сделать то, что может определить взгляд микробиолога? Вопросы по самостоятельной части. .1. Кратко обосновать применимость представленных в части для самостоятельной проработки методов в системе распознавания образа биообъекта. 2. Достоинство и недостатки методов первой и второй категории. 3. Из методов, перечисленных в конце абзаца при самостоятельной проработке выбрать только те, которые можно реализовать при анализе образа микроорганизма на МКС Вопросы. 1.Приведите примеры физиологических кривых, полученных в результате исследований человека, которые можно при определенных условиях обрабатывать с помощью 1,2,3 и опишите, что это за условия. 2. Написать основные характеристики а). случайных величин; б). случайной функции; с). случайного процесса.
Обработка гармонической функции. Гармонический анализ. Любая периодическая функция f(t) с периодом Tможет быть представлена в виде суммы синусов и косинусов от аргумента nt (так называемый ряд Фурье), где n - целое положительное число, t - время, =2/T - угловая частота.
Компоненты ряда Фурье называются гармониками. Любая четная функция может быть разложена в ряд Фурье, состоящий из косинусов, а любая нечетная функция раскладывается в ряд из синусов. Случайная функция – функция, которая в результате опыта может принять тот или иной неизвестный заранее конкретный вид. Обычно аргументом случайной функции (с.ф.) является время, тогда с.ф. называют случайным процессом (с.п.). С.ф. непрерывно изменяющегося аргумента t называется такая с.в., распределение которой зависит не только от аргумента t=t1, но и от того, какие частные значения принимала эта величина при других значениях данного аргумента t=t2. Эти с.в. корреляционно связаны между собой и тем больше, чем ближе одни к другим значения аргументов. В пределе при интервале между двумя значениями аргумента, стремящемся к нулю, коэффициент корреляции равен единице:
т.е. t1 и t1+Dt1 при Dt1®0 связаны линейной зависимостью. С.ф. принимает в результате одного опыта бесчисленное (в общем случае несчетное) множество значений – по одному для каждого значения аргумента или для каждой совокупности значений аргументов. Эта функция имеет одно вполне определенное значение для каждого момента времени. Результат измерения непрерывно изменяющейся величины является такой с.в., которая в каждом данном опыте представляет собой определенную функцию времени. С.ф. можно также рассматривать как бесконечную совокупность с.в., зависящую от одного или нескольких непрерывно изменяющихся параметров t. Каждому данному значению параметра t соответствует одна с.в Xt. Вместе все с.в. Xt определяют с.ф. X(t). Эти с.в. корреляционно связаны между собой и тем сильнее, чем ближе друг к другу. Элементарная с.ф. – это произведение обычной с.в. Х на некоторую С.ф.
Реализация с.ф. X(t) – описывается уравнением x=f1(t) при t=t1 и уравнением x=f2(t) при t=t2. Вообще функции x=f1(t) и x=f2(t) – различные функции. Но эти функции тождественны и линейны тем более, чем более (t1®t2) t1 ближе к t2. Одномерная плотность вероятности с.ф. p(x,t) – зависит от х и от параметра t. Двумерная плотность вероятности p(x1,x2;t1,t2) – совместный закон распределения значений X(t1) и X(t2) с. ф. X(t) при двух произвольных значениях t и t¢ аргумента t.
В общем случае функция X(t) характеризуется большим числом n-мерных законов распределения М.о. с.ф. X(t) - неслучайная функция
Аналогично и дисперсия - неслучайная функция. Степень зависимости с.в. для различных значений аргумента характеризуется автокорреляционной функцией. Автокорреляционная функция с.ф. X(t) - неслучайная функция двух аргументов Kx(ti,tj), которая при каждой паре значений ti, tj равна корреляционному моменту соответствующих ординат с.ф. (при i=j корреляционная функция (к.ф.) обращается в дисперсию с.ф.);
где Автокорреляционная функция - совокупность м.о. произведений отклонений двух ординат с.ф. Автокорреляционная функция характеризует степень изменчивости с.ф. при изменении аргумента. На рис. видно, что зависимость между значениями с.ф., соответствующим двум данным значениям аргумента t - слабее в первом случае.
Рис. Корреляционно связанные случайные функции Если две с.ф. X(t) и Y(t), образующие систему не являются независимыми, то тождественно не равна нулю их взаимная корреляционная функция:
где Если X(t) и Y(t) независимы, то KXY(t1,t2)=0. Система из n с.ф. X1(t), X2(t),...,Xn(t) характеризуется n м.о. Взаимная корреляционная функция (характеризует связь между двумя с.ф., т.е. стохастическую зависимость) Особое значение имеют стационарные случайные функции, вероятностные характеристики которых не меняются при любом сдвиге аргумента. М.о. стационарной с.ф. постоянно (т.е. не является функцией), а корреляционная функция зависит лишь от разности значений аргументов ti и tj.
Это четная функция (симметрично OY). Из (69.5)® При большом значении интервала времени t=t2-t1 отклонение ординаты с.ф. от ее м.о. в момент времени t2 становится практически независимым от значения этого отклонения в момент времени t1. В этом случае функция KX(t), дающая значение корреляционного момента между X(t1) и X(t2), при ½t½®¥ стремится к нулю. Многие стационарные с.ф. обладают эргодическим свойством, которое заключается в том, что при неограниченно возрастающем интервале наблюдения среднее наблюденное значение стационарной с.ф. с вероятностью, равной 1, будет неограниченно приближаться к ее м.о. Наблюдение стационарной с.ф. при разных значениях t на достаточно большом интервале в одном опыте равноценно наблюдению ее значений при одном и том же значении t в ряде опытов. Иногда требуется определить характеристики преобразованных с.ф. по характеристикам исходных с.ф. Так если
то При интегрировании или дифференцировании с.ф. получаем также с.ф. Если X(t) распределена нормально, то Z(t) и Y(t) распределены тоже нормально. Если X(t) – стационарная с.ф., то Z(t) уже не стационарная с.ф., т.к. Примеры корреляционных функций. 1) 3) 5) На графиках a = 1, b = 5, s = 1.
a - характеризует быстроту убывания корреляционной связи между ординатами с.ф. при увеличении разности аргументов этих ординат t. a/b - характеризует "степень нерегулярности процесса". При малом a/b ординаты процесса оказываются сильно коррелированными и реализация процесса похожа на синусоиду; при большом a/b периодичность с частотой b становится незаметной. Корреляционные функции 4 и 6 – не имеют производных при t=0. Соответствующие спектральные плотности: 2) 3) 4) 6) Чтобы найти корреляционную функцию интеграла (производной) от с.ф., нужно дважды проинтегрировать (продифференцировать) корреляционную функцию исходной с.ф. сначала по одному, затем по другому аргументу:
Формула (71) для стационарной функции примет вид:
Корреляционная функция с.ф. и ее производной При умножении с.ф. на детерминированную получаем с.ф. Z(t)=a(t)X(t), корреляционная функция которой равна KZ(t1,t2)=a(t1)a(t2) KX(t1,t2) (7), где a(t) - детерминированная функция. Сумма двух с.ф. является тоже с.ф. Z(t)=X(t)+Y(t) и ее корреляционная функция при наличии корреляционной связи между X(t) и Y(t): KZ(t1,t2)=KX(t1,t2)+ KY(t1,t2)+2KXY(t1,t2), (8) где KXY(t1,t2) - взаимная корреляционная функция двух зависимых с.ф. X(t) и Y(t). Если X(t) и Y(t) независимы, то KXY(t1,t2)=0. М.о. с.ф. Z(t):
Вопросы: 1. Что с точки зрения физиологии обозначают:
А).автокорреляция; Б). взаимокорреляция; В).функция переноса.
2. Перечислить ограничения обработки функций сложной волны описывающих физиологические явления.
Качество «5 М».
Вопросы: При помощи формулы качества «5 М» описать бортовой эксперимент «Уролюкс»
Пример: Исследование биологических жидких сред в микрогравитации.
1. Космонавт 2. Используемый прибор 3. Измеряемое биологическое вещество 4. Метод, поддающийся сравнению с наземными условиями 5. Окружающая среда
Факторный анализ
Факторный анализ (factor analysis) – многомерный статистический метод, применяемый для изучения взаимосвязей между значениями количественных переменных. Основная идея факторного анализа заключается в том, что имеющиеся зависимости между большим числом исходных наблюдаемых переменных определяются существованием гораздо меньшего числа скрытых или латентных переменных, называемых факторами.
Главными целями факторного анализа являются: сокращение числа переменных и определения структуры взаимосвязей между переменными. Поэтому факторный анализ используется или как метод сокращения данных или как метод классификации. Факторный анализ позволяет исследователю описать объект измерения с одной стороны всесторонне, учитывая множество исходных тесно взаимосвязанных между собой переменных, а с другой стороны компактно с помощью небольшого числа переменных.
Проведение факторного анализа предполагает обладанием базисом статистических знаний: методами описательного анализа данных, методов проверки статистических гипотез, знакомство с корреляционным и регрессионным анализом.
Факторный анализ впервые возник и применялся для измерений в психологии, но в настоящее время широко используется для решения практических задач не только в психологии, но и в социологии, политологии, экономике, медицине, маркетинге, химии и других областях.
Методы факторного анализа доступны во всех профессиональных статистических пакетах обработки данных: SPSS, SAS, R, Statistica и др.
Извлечения из математической статистики
Коэффициент взаимосвязи между некоторой переменной и общим фактором, выражающий меру влияния фактора на признак, называется факторной нагрузкой (Factor load) данной переменной по данному общему фактору. Значение (мера проявления) фактора у отдельного объекта называется факторным весом объекта по данному фактору. Процесс факторного анализа состоит из трех больших этапов: Подготовки ковариационной матрицы (Иногда вместо нее используется корреляционная матрица); Выделения первоначальных ортогональных векторов (основной этап); Вращение с целью получения окончательного решения. Подготовка к факторному анализу
При подготовке к факторному анализу часто (некоторые методы этого не требуют, но большая часть - требует) составляют ковариационные и корреляционные матрицы. Это матрицы, составленные из ковариации и корреляций векторов-атрибутов (строки и столбцы - атрибуты, пересечение - ковариация/корреляция). Метод главных компонент Метод главных компонент стремится выделить оси, вдоль которых количество информации максимально, и перейти к ним от исходной системы координат. При этом некоторое количество информации может теряться, но зато сокращается размерность. Этот метод проходит практически через весь факторный анализ, и может меняться путем подачи на вход разных матриц, но суть его остается неизменной. Основной математический метод получения главных осей - нахождение собственных чисел и собственных векторов ковариационной матрицы таких, что: RV = λV, где λ - собственное число R, R - матрица ковариации, V - собственный вектор R. Тогда: RV − λV = 0 V(R − λE) = 0 и решение есть когда: | R − λE | = 0, где R - матрица ковариации, λ - собственное число R, E - единичная матрица. Затем считаем этот определитель для матрицы соответствующей размерности. V находим, подставляя собственные числа по очереди в V(R − λE) = 0 и решая соответствующие системы уравнений. Сумма собственных чисел равна числу переменных, произведение - детерминанту корелляционной матрицы. Собственное число представляет собой дисперсию оси, наибольшее - первой и далее по убыванию до наименьшего - количество информации вдоль последней оси. Доля дисперсии, приходящаяся на данную компоненту, считается отсюда легко: надо разделить собственное число на число переменных m. Коэффициенты нагрузок для главных компонент получаются делением коэффициентов собственных векторов на квадратный корень соответствующих собственных чисел. Алгоритм NIPALS вычисления главных компонент На практике чаще всего для определения главных компонент используют итерационные методы, к примеру, NIPALS: 0. Задается 0 < ε1 < 1 - критерий окончания поиска главного компонента, и 0 < ε2 < 1 - критерий окончания поиска главных компонентов, исходная отцентрированная матрица X, i=1 - номер главной компоненты. 1. Берется T_k = x_j \in X - вектор-столбец, k - шаг алгоритма, j - любой столбец (просто чтобы было с чего начинать апроксимизацию). 2. Вектор Tk транспонируется. 3. Считается P_k = \frac {T_k^T X} {T_k^T T_k}. 4. Pk нормируется P_k=P_k (P_k^T P_k)^{-0,5} 5. Считается новый T_k^new = \frac {X P_k} {P_k^T P_k} 6. Если |T_k^{new} - T_k| < \epsilon_1, то T_k^{new} и Pk - вектора весов и нагрузок соответственно для i-ой главной компоненты. Если нет, то T_k=T_k^{new} и иди на 2. 7. X=X-T_k P_k^T. 8. Если | X | < ε, то стоп - найдены все основные компоненты, нас удовлетворяющие. Иначе i++. Иди на 1. Другие методы Метод сингулярных компонент Метод максимального правдоподобия Метод альфа-факторного анализа Вращение
Вращение - это способ превращения факторов, полученных на предыдущем этапе, в более осмысленные. Бывает графическое (проведение осей, не применяется при более чем 2мерном анализе), аналитическое (выбирается некий критерий вращения, различают ортогональное и косоугольное) и матрично-приближенное (вращение состоит в приближении к некой заданной целевой матрице). Результатом вращения является вторичная структура факторов. Первичная факторная структура (состоящая из первичных нагрузок (полученных на предыдущем этапе)) - это, фактически, проекции точек на ортогональные оси координат. Очевидно, что если проекции будут нулевыми, то структура будет проще. А проекции будут нулевыми, если точка лежит на какой-то оси. Де-факто вращение есть переход от одной системы координат к другой при известных координатах в одной системе (первичные факторы) и итеративно подбираемых координатах в другой системе (вторичных факторов). При получении вторичной структуры стремятся перейти к такой системе координат, чтобы провести через точки (объекты) как можно больше осей, чтобы как можно больше проекции (и соответственно нагрузок) были нулевыми. При этом могут сниматься ограничения ортогональности и убывания значимости от первого к последнему факторам, характерные для первичной структуры, и вторичная структура является более простой, чем первичная, и потому более ценна. Обозначим понятие простой структуры. Пусть r - число (общих) факторов первичной структуры, V - матрица вторичной структуры, состоящая из нагрузок (координат) вторичных факторов (строка - переменная из R, столбец - вторичный фактор). В каждой строке матрицы V должен быть хотя бы 1 нулевой элемент; Каждый столбец из матрицы V должен содержать не менее r нулей; У одного из столбцов из любой пары из матрицы V должно быть несколько нулевых коэффициентов(нагрузок) в тех позициях, где для другого столбца они ненулевые (для различения); При числе факторов больше 4 в каждой паре должно быть несколько нулевых нагрузок в одних и тех же строках; Для каждой пары столбцов должно быть, как можно меньше больших по величине нагрузок в одних и тех же строках. Тогда структура будет хорошо подходить для интерпретации и будет выделяться однозначно. Наипростейшей является структура, где каждая переменная имеет факторную сложность (количество факторов, которые на нее влияют и оказывают факторную нагрузку), равную 1 (все факторы будут характерными). Реально это не достижимо, и потому мы стремимся приблизится к простой структуре при помощи различных методов. Существует эмпирическое правило, что для каждого фактора по крайней мере три переменных имеют значительную на него нагрузку. Аналитическое вращение Наиболее интересно аналитическое вращение, так как позволяет получить вторичную структуру исходя из достаточно критериев и без априорного знания о структуре факторной матрицы. Ортогональное вращение Ортогональное вращение подразумевает, что мы будем вращать факторы, но не будем нарушать их ортогональности друг другу. Ортогональное вращение подразумевает умножение исходной матрицы первичных нагрузок на ортогональную матрицу R (такую матрицу, что |R|=1, R*R^T=E, R= r \times r) V=BR Алгоритм ортогонального вращения в общем случае таков: 0. B - матрица первичных факторов. 1. Ищем ортогональную матрицу RT размера 2*2 для двух столбцов(факторов) bi и bj матрицы B такую, что критерий для матрицы [bibj]R максимален. 2. Заменяем столбцы bi и bj на столбцы [b_i b_j] \times R. 3. Проверяем, все ли столбцы перебрали. Если нет, то 1. 4. Проверяем, что критерий для всей матрицы вырос. Если да, то 1. Если нет, то конец.
МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ МЕДИЦИНСКИХ ДАННЫХ.
АКТУАЛЬНОСТЬ СТАТИСТИКИ В МЕДИЦИНЕ Статистика в медицине является одним из инструментов анализа экспериментальных данных и клинических наблюдений, а также языком, с помощью которого, сообщаются полученные математические результаты. Однако, это не единственная задача статистики в медицине. Математический аппарат широко применяется в диагностических целях, решении классификационных задачи поиске новых закономерностей, для постановки новых научных гипотез. наступления события, а не самим событием. Использование статистических программ предполагает знание основных методов и этапов статистического анализа: их последовательности, необходимости и достаточности. В предлагаемом изложении основной упор сделан не на детальное представление формул, составляющих статистические методы, а на их сущность и правила применения. Статистическая обработка медицинских исследований базируется на принципе того, что верное для случайной выборки верно и для генеральной совокупности (популяции), из которой эта выборка получена. Однако выбрать или набрать истинно случайную выборку из генеральной совокупности практически очень сложно. Поэтому следует стремиться к тому, чтобы выборка была репрезентативной по отношению к изучаемой популяции, т.е. достаточно адекватно отражающей все возможные аспекты изучаемого состояния или заболевания в популяции, чему способствует чёткое формулирование цели и строгое соблюдение критериев включения и исключения как в исследование, так и в статистический анализ. ВИДЫ СТАТИСТИЧЕСКИХ ДАННЫХ В МЕДИЦИНЕ Статистические данные могут быть представлены как количественными (числовыми непрерывными или дискретными), так и качественными (категориальными порядковыми или номинальными) переменными. Необходимо чётко указывать тип (вид) переменной при заполнении базы данных и точно придерживаться выбранного типа данных, так как от этого может зависеть дальнейшая обработка переменных во многих используемых в настоящее время статистических программах. Например, нельзя одновременно вносить в столбец переменных и числовые и текстовые, даже аналогичные по смыслу, данные: если заполнение «да/нет» в виде 1 или 0, то не вносить буквенные аббревиатуры и наоборот. Количественные (числовые) данные предполагают, что переменная принимает некоторое числовое значение. Из них выделяют дискретные данные, которые могут принимать строго определённые значения, в то время как непрерывные могут быть представлены любыми значениями. Уникальным примером количественных данных является представление возраста двумя типами: в виде непрерывной переменной – указывается точный возраст пациента, и в виде дискретной переменной – указывается только количество полных лет (50,3 года и 50 лет; 50,9 года и 51 год). Категориальность является основой смыслового понимания качественных переменных. Категориальные данные применяются для описания состояния объекта путем присвоения ему номера, соответствующего категории, к которой этот объект принадлежит. Важным условием для применения категориальных данных является принадлежность одного объекта исследования только к одной возможной категории для одного критерия. Качественные номинальные данные используются в том случае, если категории не упорядочены. Числа в данном случае являются лишь обозначением для состояния объекта и не упорядочивают это состояние. Например, по полу: 1 – мужской, 2 – женский. Качественные порядковые (ранговые, ординарные) данные – данные, для которых категории могут быть упорядочены. Например, от плохого самочувствия к хорошему: 1 – хорошее, 2 – удовлетворительное, 3 – плохое. На практике часто используется перевод количественных данных в качественное категориальное упорядоченное представление, особенно при расчётах пороговых значений (cut-off) для последующих расчётов характеристик риска или прогностической значимости с использованием таблицы сопряжённости. Например, 1 – концентрация общего холестерина меньше или равна 5,2 ммоль/л (отношение рисков развития ИБС менее 1, прогности
|
|||||||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.231 (0.015 с.) |

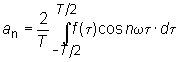
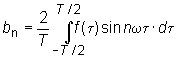
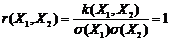 ,
,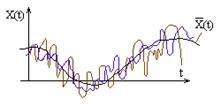 неслучайную функцию j(t): X(t)=X×j(t), т.е. такая с.ф., у которой случайным является не вид, а только ее масштаб.
неслучайную функцию j(t): X(t)=X×j(t), т.е. такая с.ф., у которой случайным является не вид, а только ее масштаб.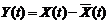 - имеет м.о. равное нулю. p[x(t1)] – плотность распределения с.в. Х (значения с.ф. X(t)), взятой при произвольном значении t1 аргумента t.
- имеет м.о. равное нулю. p[x(t1)] – плотность распределения с.в. Х (значения с.ф. X(t)), взятой при произвольном значении t1 аргумента t.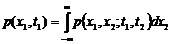
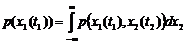 . (1)
. (1)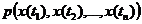 .
.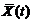 , которая при каждом значении аргумента t равна м.о. ординаты с.ф. при этом аргументе t.
, которая при каждом значении аргумента t равна м.о. ординаты с.ф. при этом аргументе t.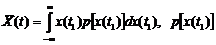 - функция, зависящая от x и t.
- функция, зависящая от x и t. (2)
(2)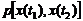 - совместная плотность распределения двух с.в. (значений с.ф.), взятых при двух произвольных значениях t1 и t2 аргумента t. При t1=t2=t получаем дисперсию D(t).
- совместная плотность распределения двух с.в. (значений с.ф.), взятых при двух произвольных значениях t1 и t2 аргумента t. При t1=t2=t получаем дисперсию D(t).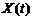 , взятых при аргументах t1 и t2, от ординат неслучайной функции м.о.
, взятых при аргументах t1 и t2, от ординат неслучайной функции м.о. 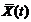 , взятых при тех же аргументах.
, взятых при тех же аргументах.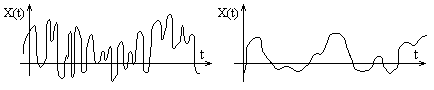
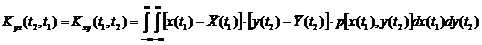 (3),
(3),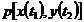 - совместная плотность распределения двух с.в. (значений двух с.ф. X(t) и Y(t)), взятых при двух произвольных аргументах (t1 - аргумент функции X(t), t2 - аргумент функции Y(t)).
- совместная плотность распределения двух с.в. (значений двух с.ф. X(t) и Y(t)), взятых при двух произвольных аргументах (t1 - аргумент функции X(t), t2 - аргумент функции Y(t)).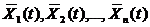 , nавтокорреляционными функциями
, nавтокорреляционными функциями 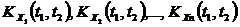 и еще n(n-1)/2 корреляционными функциями
и еще n(n-1)/2 корреляционными функциями 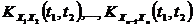 .
.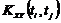 двух с.ф. X(t) и Y(t) - неслучайная функция двух аргументов ti и tj, которая при каждой паре значений ti, tj равна корреляционному моменту соответствующих сечений с.ф. Она устанавливает связь между двумя значениями двух функций (значения - с.в.), при двух аргументах t1 и t2.
двух с.ф. X(t) и Y(t) - неслучайная функция двух аргументов ti и tj, которая при каждой паре значений ti, tj равна корреляционному моменту соответствующих сечений с.ф. Она устанавливает связь между двумя значениями двух функций (значения - с.в.), при двух аргументах t1 и t2.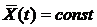 ,
, 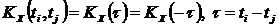 (4)
(4)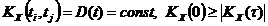 .
.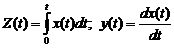 (5),
(5),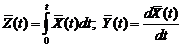 т.е. м.о. интеграла (производной) от с.ф. равно интегралу (производной) от м.о. (y(t) - скорость изменения с.ф.X(t),
т.е. м.о. интеграла (производной) от с.ф. равно интегралу (производной) от м.о. (y(t) - скорость изменения с.ф.X(t), 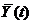 - скорость изменения м.о.).
- скорость изменения м.о.).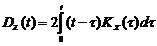 зависит от t.
зависит от t.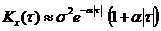 (из (2) при b®0); 2)
(из (2) при b®0); 2) 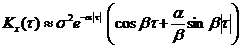 ;
;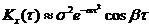 ; 4)
; 4) 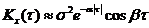 ;
;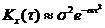 (из (3) при b®0); 6)
(из (3) при b®0); 6) 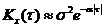 (из (4) при b®0).
(из (4) при b®0).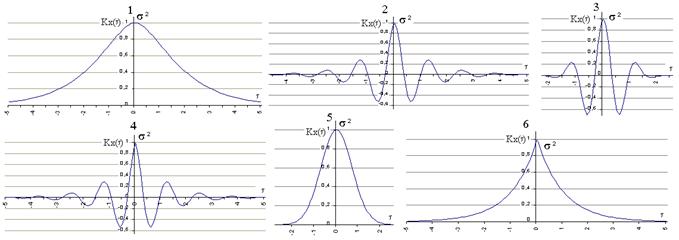
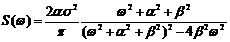 ;
; ;
;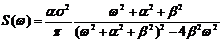 ;
; .
.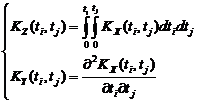 (6).
(6).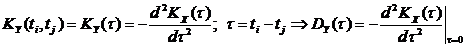 .
.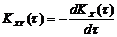 . Для дифференцируемого стационарного процесса ордината с.ф. и ее производной, взятая в тот же момент времени являются некоррелированными с.в. (а для нормального процесса и независимыми).
. Для дифференцируемого стационарного процесса ордината с.ф. и ее производной, взятая в тот же момент времени являются некоррелированными с.в. (а для нормального процесса и независимыми).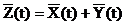 .
.