Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тест 1. Выражения. Тождества. Рациональные дроби.Содержание книги
Поиск на нашем сайте
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ОБОБЩЕНИЕ И СИСТЕМАТИЗАЦИЯ ПРОГРАММНОГО МАТЕРИАЛА ЗА КУРС ОСНОВНОЙ ШКОЛЫ (12 часов)
ТЕСТЫ Тест 1. Выражения. Тождества. Рациональные дроби. Вариант 1 1. Найдите значение выражения
2. Упростите выражение
3. Разложите на множители многочлен
4. Сократите дробь
5. Упростите выражение
Вариант 2 1. Найдите значение выражения
2. Упростите выражение
3. Разложите на множители многочлен
4. Сократите дробь
5. Упростите выражение
Ответы: Вариант 1:1 А, 2 Б, 3 Г, 4 В, 5 А. Вариант 2: 1 В, 2 А, 3 В, 4 Г, 5 А. Тест 2. Степень с целым показателем. Свойства степени. Вариант 1 1. Найдите значение выражения
2. Упростите выражение
3. Вычислите значение выражения
4. Упростите
5. Стороны прямоугольника
Вариант 2. 1. Найдите значение выражения
2. Упростите выражение
3. Вычислите значение выражения
4. Упростите
5. Стороны прямоугольника
Ответы: Вариант 1:1 Б, 2 Г, 3 А, 4 В, 5 Б. Вариант 2: 1 А, 2 Б, 3 Г, 4 А, 5 Г. Тест 3. Квадратный корень, его свойства. Вариант 1 1. Найдите значение выражения
2. Упростите выражение
3. Внесите множитель под знак корня
4. Избавьтесь от иррациональности в знаменателе дроби
5. Сократите дробь
Вариант 2 1. Найдите значение выражения
2. Упростите выражение
3. Внесите множитель под знак корня
4. Избавьтесь от иррациональности в знаменателе дроби
5. Сократите дробь
Ответы: Вариант 1:1 А, 2 Б, 3 В, 4 А, 5 Г. Вариант 2: 1 Б, 2 В, 3 Г, 4 А, 5 Г. Тест 4. Уравнения и их системы. Вариант 1 1. Решите систему уравнений
2. Решите уравнение
3. Составьте квадратное уравнение с корнями 2 и – 3.
4. При каких значениях а дробь
5. Какая фигура является графиком уравнения
Вариант 2 1. Решите систему уравнений
2. Решите уравнение
3. Составьте квадратное уравнение с корнями 3 и – 4.
4. При каких значениях а дробь
5. Какая фигура является графиком уравнения
Ответы: Вариант 1: 1 А, 2 В, 3 Г, 4 Б, 5 Г. Вариант 2: 1 В, 2 Г, 3 Б, 4 А, 5 В. Вариант 1 1. Оцените значение выражения
2. Сравните выражения А и В, если
3. Решите неравенство
4. Решите систему неравенств
5. Известны границы длины а и ширины b прямоугольной формы:
Вариант 2 1. Оцените значение выражения
2. Сравните выражения А и В, если
3. Решите неравенство
4. Решите систему неравенств
5. Известны границы длины а и ширины b прямоугольной формы:
Ответы: Вариант 1: 1 Г, 2 Б, 3 А, 4 А, 5 В. Вариант 2: 1 Б, 2 В, 3 Г, 4 Б, 5 А. Вариант 1 1. Найдите область определения функции
2. Укажите нули функции
4. С помощью графика функции
5. Среди данных функций выберите четную.
Вариант 2 1. Найдите область определения функции
2. Укажите нули функции
4. С помощью графика функции
5. Среди данных функций выберите нечетную.
Ответы: Вариант 1: 1 Г, 2 Б, 3 В, 4 А, 5 Г. Вариант 2: 1 Б, 2 Г, 3 А, 4 В, 5 В. Вариант 1
2. Найдите координаты вершины параболы
3. Определите наибольшее значение функции
4. Найдите промежуток убывания функции
5. При каких значениях х значения функции
Вариант 2
2. Найдите координаты вершины параболы
3. Определите наименьшее значение функции
4. Найдите промежуток возрастания функции
5. При каких значениях х значения функции
Ответы: Вариант 1: 1 Б, 2 А, 3 В, 4 А, 5 В. Вариант 2: 1 В, 2 Г, 3 Г, 4 Б, 5 А. Вариант 1 1. Решите неравенство
2. Найдите множество решений неравенства
3. Решите неравенство методом интервалов
4. Найдите область определения функции
А) Б) В) Г) Вариант 2 1. Решите неравенство
2. Найдите множество решений неравенства
3. Решите неравенство методом интервалов
4. Найдите область определения функции
А) Б) В) Г) Ответы: Вариант 1: 1 Г, 2 Б, 3 В, 4 В, 5 А. Вариант 2: 1 В, 2 Г, 3 Б, 4 Г, 5 А. Вариант 1 1. Первый член и разность арифметической прогрессии
2. Найдите сумму первых восемнадцати членов арифметической прогрессии, заданной формулой
3. Найдите первый член геометрической прогрессии
4. Найдите сумму шести первых членов геометрической прогрессии – 10; – 20; – 40; ….
5. В арифметической прогрессии
Вариант 2 1. Первый член и разность арифметической прогрессии
2. Найдите сумму первых шестнадцати членов арифметической прогрессии, заданной формулой
3. Найдите первый член геометрической прогрессии
4. Найдите сумму семи первых членов геометрической прогрессии – 12; – 24; – 48; ….
5. В арифметической прогрессии
Ответы: Вариант 1: 1 Б, 2 Б, 3 А, 4 В, 5 Г. Вариант 2: 1 В, 2 А, 3 Г, 4 Б, 5 Б. Вариант 1 1. Оля решила послать пять открыток пяти разным подругам. Сколькими способами она может это сделать?
2. Компания из 5 человек заходит в автобус, в котором имеется 7 свободных мест. Сколько есть способов рассадить вошедших пассажиров по свободным места?
3. Какова вероятность того, что при бросании игрального кубика выпадет более 4 очков?
4. В ящике лежит 8 цветных карандашей и 2 черных. Какова вероятность того, что наугад выбранные два карандаша будут цветными?
5. Имеется 300 способов выбрать двух дежурных из учеников класса. Сколько учеников в классе?
Вариант 2 1. Шести игрокам команды раздали майки с номерами от 1 до 6. Сколькими способами это можно сделать?
2. В конце экзамена у экзаменатора осталось 12 билетов. Сколько имеется способов выдать 3 билета трем опоздавшим студентам?
3. Какова вероятность того, что при бросании игрального кубика выпадет менее 4 очков?
4. В ящике лежит 8 цветных карандашей и 2 черных. Какова вероятность того, что наугад выбранные три карандаша будут цветными?
5. Выбрать трех дежурных из учеников класса можно в 9 раз большим числом способов, чем выбрать двух дежурных. Сколько учеников в классе?
Ответы: Вариант 1: 1 А, 2 Г, 3 В, 4 Б, 5 Б. Вариант 2: 1 В, 2 А, 3 Г, 4 Б, 5 В. Вариант 1 I часть Выполните задания 1 – 5 и запишите правильный ответ. Верный ответ каждого задания оценивается одним баллом. 1. Выполните действие Ответ: ________________________ 2. Вычислите Ответ: ________________________ 3. Упростите выражение
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.249.232 (0.009 с.) |

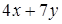 при
при 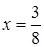 ,
, 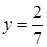 .
.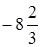 ;
;
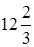 .
.
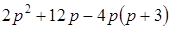 .
.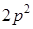 ;
;
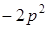 ;
;
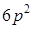 ;
;
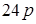 .
.
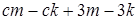 .
.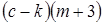 ;
;
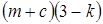 ;
;
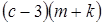 ;
;
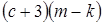 .
.
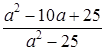 .
.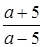 ;
;
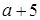 ;
;
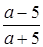 ;
;
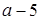 .
.
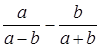 .
.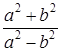 ;
;
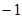 ;
;
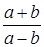 ;
;
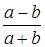 .
.
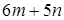 при
при 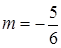 ,
, 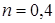 .
.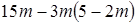 .
.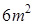 ;
;
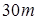 ;
;
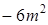 ;
;
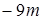 .
.
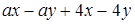 .
.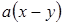 ;
;
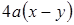 ;
;
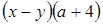 ;
;
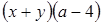 .
.
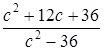 .
.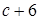 ;
;
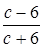 ;
;
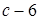 ;
;
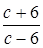 .
.
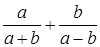 .
.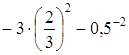 .
.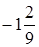 ;
;
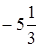 ;
;
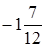 ;
;
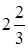 .
.
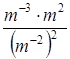 .
.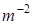 ;
;
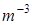 ;
;
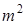 ;
;
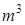 .
.
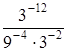 .
.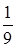 ;
;
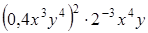 .
.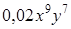 ;
;
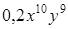 ;
;
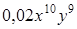 ;
;
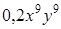 .
.
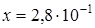 м и
м и 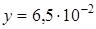 м. Найдите периметр прямоугольника.
м. Найдите периметр прямоугольника.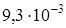 м;
м;
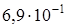 м;
м;
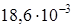 м;
м;
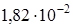 м.
м.
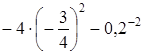 .
.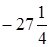 ;
;
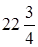 ;
;
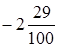 ;
;
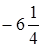 .
.
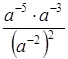 .
.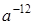 ;
;
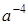 ;
;
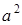 ;
;
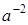 .
.
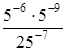 .
.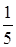 .
.
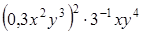 .
.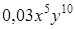 ;
;
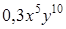 ;
;
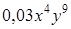 ;
;
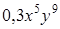 .
.
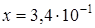 м и
м и 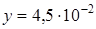 м. Найдите периметр прямоугольника.
м. Найдите периметр прямоугольника.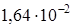 м;
м;
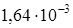 м;
м;
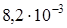 м;
м;
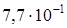 м.
м.
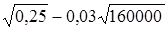 .
.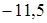 ;
;
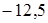 ;
;
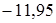 ;
;
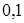 .
.
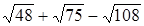 .
.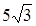 ;
;
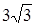 ;
;
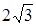 ;
;
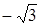 .
.
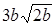 .
.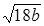 ;
;
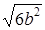 ;
;
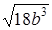 ;
;
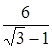 .
.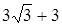 ;
;
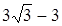 ;
;
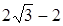 ;
;
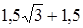 .
.
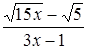 .
.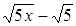 ;
;
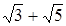 ;
;
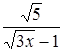 ;
;
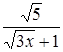 .
.
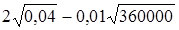 .
.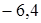 ;
;
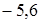 ;
;
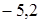 ;
;
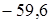 .
.
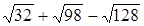 .
.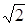 ;
;
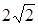 ;
;
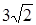 ;
;
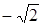 .
.
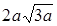 .
.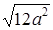 ;
;
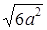 ;
;
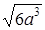 ;
;
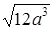 .
.
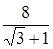 .
.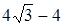 ;
;
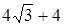 ;
;
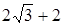 .
.
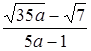 .
.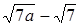 ;
;
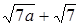 ;
;
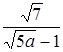 ;
;
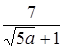 .
.
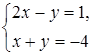 . В ответ запишите 20% от х и 10% от у.
. В ответ запишите 20% от х и 10% от у.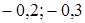 ;
;
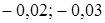 ;
;
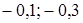 ;
;
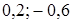 .
.
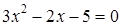 .
.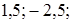
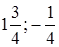 ;
;
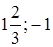 ;
;
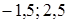 .
.
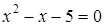 ;
;
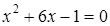 ;
;
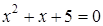 ;
;
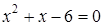 .
.
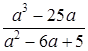 равна 0.
равна 0.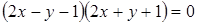 ?
?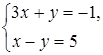 . В ответ запишите 30% от х и 10% от у.
. В ответ запишите 30% от х и 10% от у.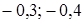 ;
;
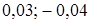 ;
;
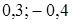 ;
;
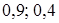 .
.
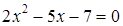 .
.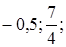
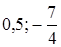 ;
;
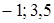 ;
;
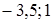 .
.
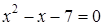 ;
;
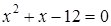 ;
;
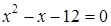 ;
;
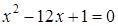 .
.
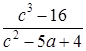 равна 0.
равна 0.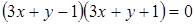 ?
?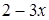 , если
, если 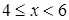 .
.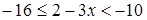 ;
;
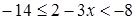 ;
;
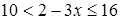 ;
;
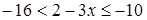 .
.
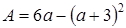 и
и 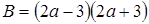 .
.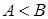 ;
;
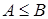 ;
;
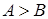 ;
;
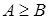 .
.
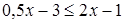 .
.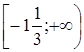 ;
;
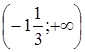 ;
;
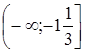 ;
;
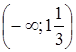 .
.
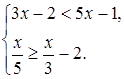
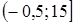 ;
;
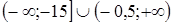 ;
;
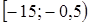 ;
;
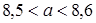 ,
, 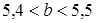 . Оцените периметр Р комнаты.
. Оцените периметр Р комнаты.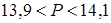 ;
;
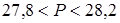 ;
;
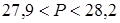 ;
;
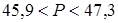 .
.
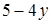 , если
, если 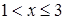 .
.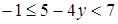 ;
;
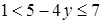 ;
;
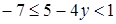 ;
;
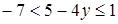 .
.
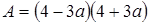 и
и 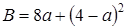 .
.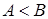 ;
;
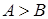 ;
;
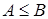 ;
;
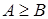 .
.
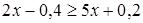 .
.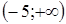 ;
;
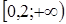 ;
;
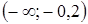 ;
;
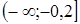 .
.
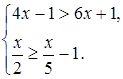
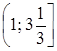 ;
;
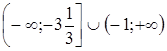 ;
;
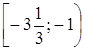 ;
;
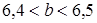 . Оцените периметр Р комнаты.
. Оцените периметр Р комнаты.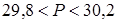 ;
;
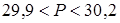 ;
;
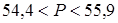 ;
;
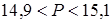 .
.
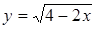 .
.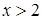 ;
;
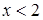 ;
;
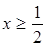 ;
;
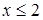 .
.
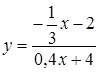 .
.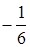 .
.
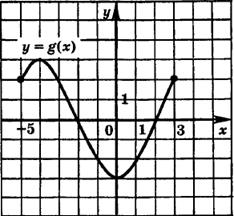 3. По рисунку определите все значения х, при которых функция
3. По рисунку определите все значения х, при которых функция 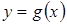 принимает положительные значения.
принимает положительные значения.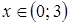 ;
;
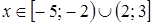 ;
;
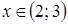 ;
;
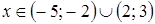 .
.
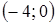 ;
;
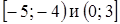 ;
;
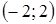 ;
;
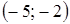 .
.
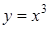 ;
;
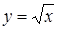 ;
;
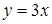 ;
;
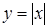 .
.
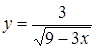 .
.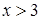 ;
;
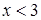 ;
;
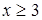 ;
;
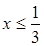 .
.
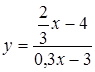 .
.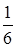 ;10;
;10;
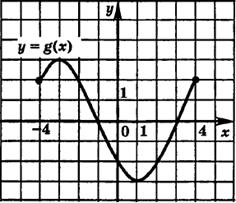 3. По рисунку определите все значения х, при которых функция
3. По рисунку определите все значения х, при которых функция 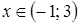 ;
;
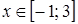 ;
;
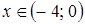 ;
;
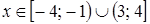 .
.
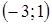 ;
;
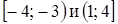 ;
;
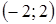 ;
;
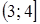 .
.
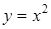 ;
;
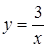 ;
;
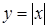 .
.
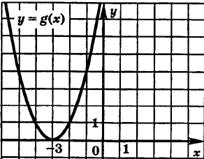 1. Укажите функцию, график которой изображен на рисунке.
1. Укажите функцию, график которой изображен на рисунке.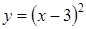 ;
;
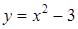 ;
;
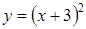 ;
;
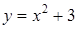 .
.
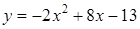 .
.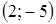 ;
;
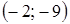 ;
;
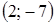 ;
;
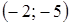 .
.
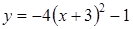 .
.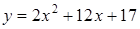 .
.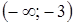 ;
;
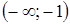 ;
;
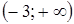 ;
;
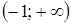 .
.
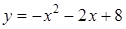 положительны?
положительны?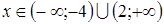 ;
;
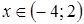 ;
;
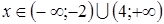 ;
;
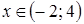 .
.
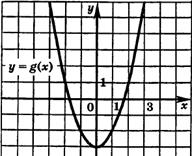 1. Укажите функцию, график которой изображен на рисунке.
1. Укажите функцию, график которой изображен на рисунке.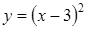 ;
;
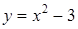 ;
;
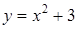 .
.
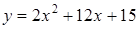 .
.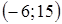 ;
;
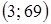 ;
;
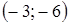 ;
;
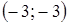 .
.
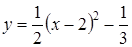 .
.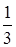 ;
;
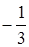 .
.
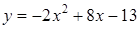 .
.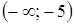 ;
;
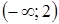 ;
;
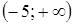 ;
;
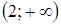 .
.
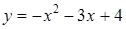 отрицательны?
отрицательны?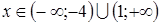 ;
;
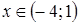 ;
;
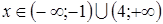 ;
;
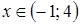 .
.
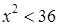 .
.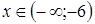 ;
;
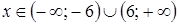 ;
;
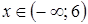 ;
;
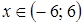 .
.
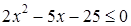 .
.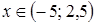 ;
;
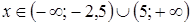 ;
;
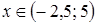 ;
;
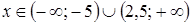 .
.
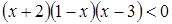 .
.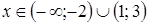 ;
;
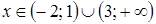 ;
;
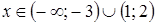 ;
;
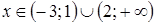 .
.
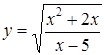 .
.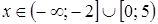 ;
;
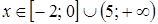 ;
;
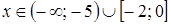 ;
;
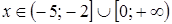 .
.
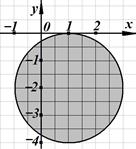 5. Решение какого неравенства изображено на рисунке?
5. Решение какого неравенства изображено на рисунке?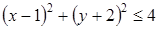 ;
; 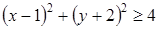 ;
;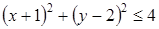 ;
; 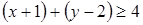 .
.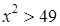 .
.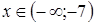 ;
;
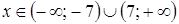 ;
;
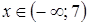 ;
;
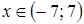 .
.
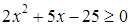 .
.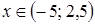 ;
;
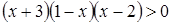 .
.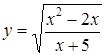 .
.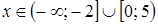 ;
;
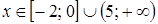 ;
;
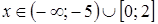 ;
;
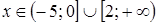 .
.
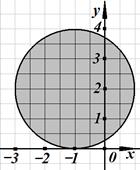 5. Решение какого неравенства изображено на рисунке?
5. Решение какого неравенства изображено на рисунке?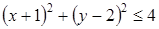 ;
; 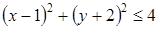 ;
;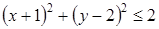 ;
; 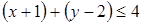 .
.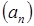 равны соответственно 2 и – 3. Найдите шестой член этой прогрессии.
равны соответственно 2 и – 3. Найдите шестой член этой прогрессии. .
.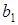 ,
, 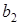 , 4, – 8, ….
, 4, – 8, ….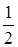 .
.
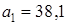 и
и 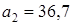 . На каком месте (укажите номер) стоит первое отрицательное число? Найдите это число.
. На каком месте (укажите номер) стоит первое отрицательное число? Найдите это число.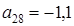 ;
;
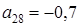 ;
;
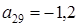 ;
;
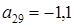 .
.
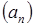 равны соответственно 5 и –2. Найдите седьмой член этой прогрессии.
равны соответственно 5 и –2. Найдите седьмой член этой прогрессии.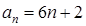 .
.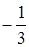 ;
;
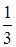 .
.
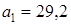 и
и 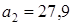 . На каком месте (укажите номер) стоит первое отрицательное число? Найдите это число.
. На каком месте (укажите номер) стоит первое отрицательное число? Найдите это число.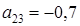 ;
;
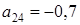 ;
;
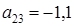 ;
;
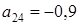 .
.
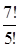 ;
;
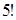 ;
;
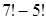 ;
;
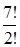 .
.
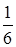 ;
;
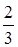 ;
;
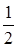 .
.
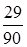 ;
;
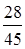 ;
;
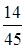 ;
;
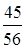 .
.
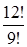 ;
;
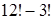 ;
;
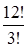 .
.
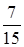 ;
;
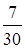 ;
;
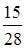 .
.
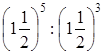 .
.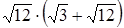 .
.