
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравновешивание сил инерции масс, движущихся возвратно-поступательноСодержание книги
Поиск на нашем сайте
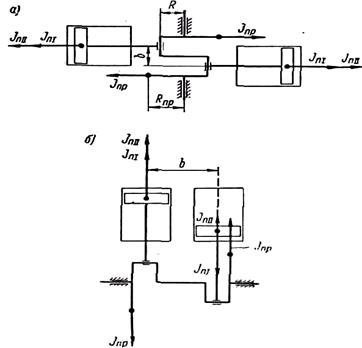
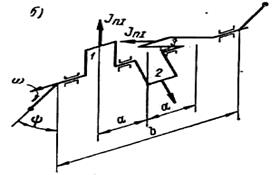
Для полного уравновешивания сил инерции и моментов масс тs движущихся возвратно-поступательно, необходимо было бы создать в компрессоре специальный механизм, движущий соответствующие уравновешивающие массы в противоположных направлениях. Но такое устройство значительно усложнило бы машину, поэтому оно не могло найти применения. В однорядном компрессоре силы инерции 2-го порядка JnΙΙ обычно не уравновешиваются. Частично можно уравновесить только силы инерции 1-го порядка JnΙ дополнительными противовесами, помещенными на концах щек, противоположных кривошипной шейке вала. При этом, когда поршень будет находиться в наружной или внутренней мертвых точках, центробежные силы инерции противовеса будут направлены в сторону, противоположную силам инерции поступательного движения JnΙ и, следовательно, будут уравновешивать их. При всех других положениях поршня (например, при повороте вала на 90°) силы инерции JnΙ, по-прежнему будут действовать вдоль оси цилиндра компрессора, хотя их величина и будет меньшей, тогда как Jnp будут действовать под углом, равным углу поворота вала, и будут являться неуравновешенными силами, вызывающими колебания машин. Дополнительными противовесами обычно в таких машинах уравновешивается только ½· JnΙ. При этом, когда вал повернется на 90˚ или на 270°, величина JnΙ = 0, но при этих углах поворота в горизонтальной плоскости будет действовать от дополнительных противовесов сила Jnp = ½· JnΙ которая сама будет неуравновешена. При таком частичном уравновешивании однорядной машины амплитуда колебаний неуравновешенных сил уменьшается в два раза. Дополнительные противовесы обычно выполняются заодно с противовесами, необходимыми для уравновешивания силы JR. В двухрядных горизонтальных машинах при смещении кривошипов на 180° (фиг. 48, а) и при равных симметрично движущихся массах в обоих рядах силы инерции JnΙ и JnΙΙ полностью уравновешиваются, но остается неуравновешенным их момент, максимальная величина которого равна
В машинах, выполненных по схеме фиг. 48, б и имеющих по рядам равные массы ms, силы JnΙ взаимно уравновешиваются. Силы инерции JnΙΙ остаются неуравновешенными, и максимальная величина их будет
Максимальный неуравновешенный момент от сил JnΙ будет
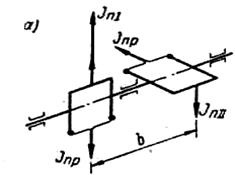
При прочих равных условиях неуравновешенный момент от силы JnΙ у машины, выполненной по схеме фиг. 48, а, будет меньше, чем у машины по схеме фиг. 48, б, так как в последнем случае плечо сил b всегда будет больше, чем в первом, вследствие одностороннего размещения цилиндров относительно линии коленчатого вала. Неуравновешенные моменты сил Мнеур в указанных схемах в значительной мере (до 50%) могут быть уменьшены силами инерции дополнительных противовесов Jnp, закрепленных на концах, противоположных шейке коленчатого вала, как это указано на фиг. 48. В многорядных компрессорах аналогичной конструкции взаимное уравновешивание сил инерции может быть достигнуто путем рациональной компоновки рядов. Рассмотрим схему двухрядного компрессора с параллельными осями цилиндров, установленных с одной стороны вала (фиг. 49, а); колена расположены под углом 90°. Максимальные силы инерции будут в 1-м ряду и во 2-м ряду и
Фиг. 48. Схемы действия сил инерции JnΙ и JnΙΙ в двухрядных компрессорах.
Неуравновешенные силы инерции в такой схеме равны JnΙ. Эти силы частично могут быть уравновешены дополнительными противовесами. Силы же инерции 2-го порядка JnΙΙ и их момент msω2Rλшb не уравновешиваются и остаются свободными. Таким образом, в двухрядных компрессорах с углом между кривошипами 90° нельзя достигнуть хорошего уравновешивания сил инерции. В этом отношении лучшей будет схема с углом между кривошипами в 180°. Однако диаграмма тангенциальных сил в компрессорах двойного действия с углом между кривошипами 90° получает такой характер, который обусловливает при той же степени неравномерности меньший маховой момент, а следовательно, и более легкий маховик. Поэтому схема со смещением кривошипов на 90° применяется для крупных компрессоров с малым числом оборотов. Для многооборотных машин более целесообразной является схема с кривошипами, смещенными на 180°.
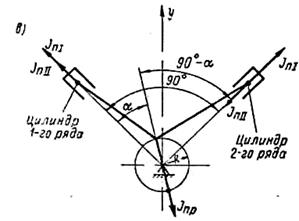
На фиг. 49, б показан трехколенный вал компрессора с параллельными осями цилиндров и односторонним их расположением относительно оси вала. Колена размещены под углом 120°. При угле α = 0 в 1-м ряду
Одновременно во втором ряду будет
В третьем ряду
Суммируя эти силы, при равенстве масс тs во всех трех рядах, получим Σ JnΙ == 0 и Σ JnΙΙ = 0. Таким образом, в рассматриваемой схеме возможно полностью взаимно уравновесить силы инерции 1-го и 2-го порядков. Сумма же моментов от сил инерции не уравновешивается, возникает продольный свободный момент от сил JnΙ и JnΙΙ. В компрессорах производится уравновешивание только момента 1-го порядка. Наиболее целесообразным методом здесь следует считать уравновешивание посредством установки двух противовесов на концах вала (фиг. 49, б). Величину результирующего момента определим как сумму моментов сил JnΙΙ относительно середины третьего колена.
Фиг. 49. Схемы действия сил инерции JnΙ и JnΙΙ в компрессорах, выполненных по различным схемам.
Момент силы JnΙ первого колена, равный 2 JnΙ · а, действует в плоскости этого же колена. Действие силы Jп1 второго колена создает момент Jп1 a, действующий в плоскости второго колена. Сумма этих моментов дает результирующий момент [93].
Плоскость действия результирующего момента определяется углом ψ (между плоскостью первого колена и плоскостью действия МJΙ):
откуда
Если в плоскости действия момента МJΙ установить два противовеса по концам вала на плече b, то он может быть уравновешен. Массу противовеса можно определить из условия
следовательно,
Если в компрессоре, выполненном по схеме фиг. 54, а, массы ms, поршневых групп первой ступени равны между собой и сумма их равна массе симметрично движущихся поршней второй ступени, т. е. 2тs1 = ms11, то достигается полное взаимное уравновешивание сил инерции 1-го и 2-го порядков без применения дополнительных противовесов. Здесь также отсутствует и неуравновешенный момент. Вышеуказанное равенство может быть достигнуто, если поршни первых ступеней изготовить из легких сплавов (например, из силумина), а поршень второй ступени из чугуна. Хорошее уравновешивание сил инерции в двухрядном компрессоре получается при расположении осей цилиндров под углом 90°. Рассмотрим схему фиг. 49, в. Если в этой схеме массы обоих рядов, движущиеся возвратно-поступательно, равны между собой (что в большинстве конструкций удается осуществить), то при повороте вала на угол α, получим для 1-го ряда
для 2-го ряда и Геометрическая сумма этих сил даст равнодействующие
и
Из уравнения для Σ Jn1 следует, что равнодействующая от сил инерции 1-го порядка при равенстве масс по рядам постоянна по величине и направлена по радиусу кривошипа. Следовательно, она легко уравновешивается путем увеличения массы противовесов, устанавливаемых на щеках колена вала для уравновешивания сил JR. Величина добавочной массы противовеса определяется из равенства
откуда добавочная масса противовеса
Силы инерции 2-го порядка равны по величине и направлены вдоль осей своих цилиндров в противоположные стороны. Величина равнодействующей Σ JnΙ1 будет меняться по гармоническому закону.
Угол между осью у (фиг. 49, в) и направлением равнодействующей может иметь лишь два значения: 90 и 270°. Следовательно, равнодействующая сил JnΙ1 всегда расположена горизонтально и может быть уравновешена только с помощью специальных устройств, которые вследствие сложности их выполнения практически не находят применения. Так как в этой схеме цилиндры компрессора расположены в одной плоскости, то продольный свободный момент от неуравновешенных сил JnΙ1 не возникает. Проанализировав (аналогично вышеизложенному) действия сил инерции 1-го и 2-го порядков Jn1 и JnΙ1 для компрессора, выполненного по любой схеме, можно найти возникающие во время работы машины ΣЈп1 и ΣЈп11 по величине и направлению. Анализ покажет, могут ли взаимно уравновешиваться силы инерции и их моменты. Если взаимной уравновешенности нет, то подобным анализом можно установить, какая неуравновешенность будет в машине при данной ее схеме и как и в какой мере она может быть уменьшена противовесами. Так, например, для трехрядных компрессоров, выполненных по W -образной схеме с углом 60° между осями цилиндров и одним общим кривошипом (фиг. 51, г), анализ дает следующие результаты. Вертикальные и горизонтальные составляющие JnΙ меняются по закону эллипса. Причем малая полуось этого эллипса вертикальна и равна
Большая полуось горизонтальна и при одинаковых массах обоих цилиндров первой ступени равна
Полное уравновешивание этих сил может быть достигнуто противовесами только тогда, когда массы, движущиеся возвратно-поступательно, у всех трех рядов будут равны между собой. Силы инерции 2-го порядка JnΙ1 в рассматриваемой схеме не уравновешиваются. Вектор геометрической суммы этих сил вращается в сторону вращения вала с удвоенной угловой скоростью. Величина его изменяется по закону эллипса, малая полуось которого вертикальна и равна
а большая полуось горизонтальна и равна
Для компрессоров, выполненных по W-образной схеме с углом 60° между осями цилиндров и с двумя кривошипами, расположенными под углом 180° друг относительно друга (фиг. 42, д), анализ действия сил инерции дает следующие результаты. Если ms11 = 0,5 ms1, то вертикальная составляющая геометрической суммы сил инерции 1-го и 2-го порядков обращается в нуль; здесь ms11 — масса среднего ряда, ms1 — масса наклонного ряда. Горизонтальные же их составляющие взаимно не уравновешиваются и остаются свободными так же, как и моменты составляющих сил инерции, действующих в вертикальной плоскости. В этой схеме не достигается полного уравновешивания сил инерции. Однако достоинствами ее являются возможность частичного уравновешивания силы JnΙ без дополнительных противовесов и хорошая диаграмма тангенциальных усилий.
В шестирядной машине с параллельными рядами цилиндров, расположенных по одну сторону вала, шестиколенчатый вал может быть выполнен с углами между коленами в 60 или 120°. В обоих случаях, если движущиеся массы по рядам равны между собой, геометрические суммы сил инерции 1-го и 2-го порядков равны нулю, т. е. силы инерции полностью взаимно уравновешиваются. Причем угол 60° дает лучшую диаграмму тангенциальных усилий.
Питання: За яким критерієм оцінюється досконалість камери згоряння з точки зору забезпечення надійності деталей вузла турбіни? При відомих значеннях температур визначити досконалість камери згоряння якщо: температура повітря за компресором температури газового потоку у 5-ті радіальних перетинах перед турбіною Відповідь: Досконалість камери згоряння оцінюється радіальною нерівномірністю температурного полю газу
При
Питання: Покажіть, як можна визначити відцентрову силу, що діє на робочу лопатку осьового турбокомпресору. Відповідь:
Питання: Назвіть переваги крейцкопфних оппозитних компресорів перед іншими конструктивними схемами поршневих компресорів. Відповідь: Крейцкопфні оппозитні компресори у порівнянні з іншими конструктивними схемами поршневих компресорів краще врівноважені.
Питання: В чому сутність експериментального способу визначення масового полярного моменту інерції. Накресліть схему дослідної установки для визначення масового полярного моменту інерції. Пояснити її конструктивні особливості. Як що масовий полярний момент інерції, отриманий експериментально, Ј р(експ).= 100 кг м2, а визначений за розрахунком Ј р(розр).=120 кг м2, то достатня лі точність розрахункового методу? Відповідь: З існуючої залежності між масовим полярним моментом інерції та періодом крутильних коливань ротора, що підвішаний на біфілярної підвісці відомо, що Якщо
1 – кронштейн; 2 – трос біфілярної підвіски; 3 – траверса підвіски; 4 – ротор компресора або турбіни.
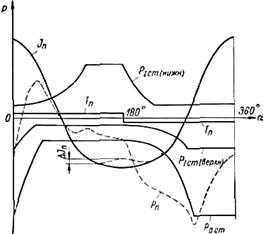
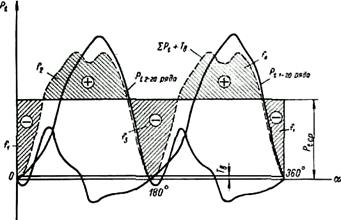
Питання: При яких розрахунках на міцність застосовується діаграма поршневих сил ряду, а при яких діаграма тангенційних сил? Відповідь: Діаграма поршневих сил ряду застосовується при розрахунку колінчатого (кривошипного) валу. Діаграма сумарних тангенційних сил застосовується при динамічному розрахунку компресора (поршневого двигуна), тобто при розрахунку маховика.
Діаграма поршневих сил ряду
Діаграма сумарних тангенційних сил
Питання: Чому моментна характеристика турбіни при запуску ГТУ має в основному лінійний характер? Відповідь: Тому що паливний автомат запуску підтримує таку подачу пального, при якої температура газу перед турбіною має постійне максимально допустиме значення. І тільки перед виходом двигуна на режим холостого ходу регулятор зменшує подачу пального, що призводить до зменшення температури газу перед турбіною і до появи криволінійної ланки на моментній характеристиці турбіни.
Питання: Які чинники впливають на частоту власних коливань лопатки компресора або турбіни? Відповідь: На частоту власних коливань лопатки компресора або турбіни впливають їх геометричні характеристики: клиновидність, трапецевидність, закрутка пера, вигін профілю, спосіб кріплення і форма коливань, а також експлуатаційні фактори: температура і частота обертання.
Питання: Поясніть способи охолодження елементів вузла турбіни. Відповідь: Основними елементами вузла турбіни, що охолоджуються, є лопатки, диски, вали, опори і корпуси. Для їх охолодження застосовують повітряні і рідинні системи. Повітряні системи охолодження притаманні для охолодження корпусів, соплових та робочих лопаток, а також дисків та фланців валів турбін. Рідинні (масляні) притаманні опорам турбін. Найбільш термічно навантаженими є лопатки турбін. для них застосовують наступні способи охолодження: радіаторний, конвективний, заградительно-плівковий, пористий. В зв’язку з цим робочі лопатки мають три основних типа конструкції: з внутрішніми каналами, з дефлектором і гільзові. Найбільш проста технологія виготовлення лопаток з каналами, що забезпечують радіальну течію повітря. Однак нерівномірність температур лопатки при цьому може досягати 150…200К (найбільш нагрітими є вхідна і вихідна крайки лопатки, де практично не можливо розташувати необхідну кількість каналів). Нерівномірність охолодження може бути зменшена за рахунок петлевої схеми руху повітря. Ще біль ефективне охолодження досягається у лопатках з інтенсифікаторами тепловіддачі, у якості яких застосовують штирки. Вони забезпечують турбулізацію потоку повітря, що суттєво підвищує коефіцієнт тепловіддачі. У лопатках з дефлектором може бути організовано як радіальний рух повітря, так і осьовий. Гільзова (оболонкова) лопатка складається з силового стриженя, до якого прикріплена оболонка, що утворює профільну частину пера лопатки. Такий спосіб охолодження дозволяє реалізувати пористе охолодження. При пористому охолодженні оболонка виготовлюється навивкою з жароміцного дроту, що спікається потім для отримання пористої структури, або з набору сітчастих листів.
Питання: Ви виконуєте запуск ГТУ і виявляєте, що час запуску більше встановленого для цього типу ГТУ. Ваше завдання: – пояснити можливі причини подовженого часу запуску ГТУ; – визначити у загальному вигляді момент прискорення під час запуску ГТУ; – поясніть, як момент прискорення пов'язаний з часом запуску. Відповідь:
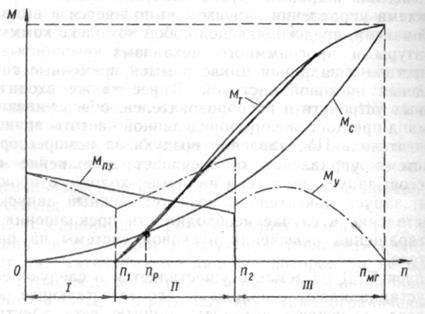
Моментна характеристика запуску ГТУ
З моментної характеристики бачимо, продовжність запуску залежить від пускового пристрою, стану ротора турбокомпресора, що розкручується. Якщо джерело живлення для пускового пристрою буде слабким, то момент пускового пристрою буде меншим за оптимальний, що призведе до продовжного часу запуску. Стан турбіни та компресора ротора, що розкручується, також впливає на відповідні моменти, що призводить до продовжного часу запуску. Момент прискорення залежить від масового полярного моменту інерції та прискорення обертів ротора, що розкручується. Тобто
Питання: Поясніть різницю у розрахунку на міцність рухомих та нерухомих лопаток турбокомпресора. Від чого залежить момент згинання, що діє на лопатки напрямних, спрямних та соплових апаратів? Відповідь: Рухомі лопатки рахуються, як від дії відцентрових сил власних мас, так і газових навантажень, що призводять до їх згинання. Нерухомі лопатки рахуються тільки від дії на них газових навантажень. Моменти згинання, що діють на нерухомі лопатки турбокомпресора, залежать від способу їх кріплення, тобто враховують конструктивний тип лопатки: консольна, рамна, двоопорна з шарнірним кріпленням у бандажних кільцях, або один кінець спирається на бандажне кільце шарнірно, а другій закріплений жорстко.
Питання: Поясніть причину деформацій передньої та задньої крайок лопаток турбін в експлуатації. Відповідь: Причиною є перегрівання вказаних крайок, в результаті чого виникають значні температурні напруження, які додаються до інших нормальних напружень, що призводить до суттєвого зменшення коефіцієнту запасу міцності і температурним деформаціям.
Питання: Як дослідним шляхом визначається власна частота коливань робочої лопатки турбокомпресора? Зобразіть експериментальну установку для даного дослідження.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-25; просмотров: 246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.104.73 (0.012 с.) |
||||||||||||||||||||||||

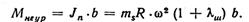 (298)
(298)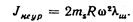 (299)
(299)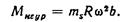 (300)
(300)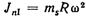
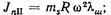
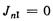
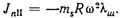
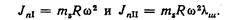
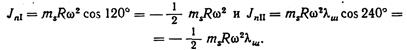
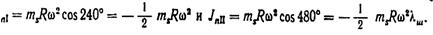
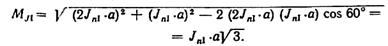
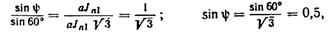
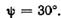
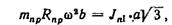
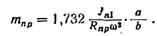
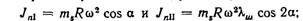
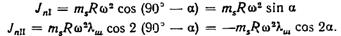
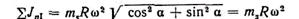
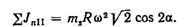
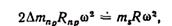
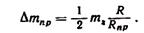
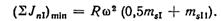
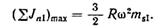
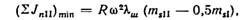
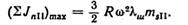
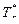 = 400 К;
= 400 К;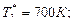
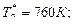
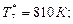
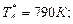
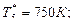 причому середньомасова температура газу визначається за наступною емпіричною залежністю:
причому середньомасова температура газу визначається за наступною емпіричною залежністю: 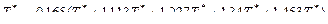 .
.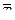 :
: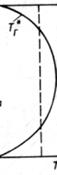
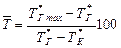 . Для сучасних камер згоряння
. Для сучасних камер згоряння 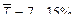 .
.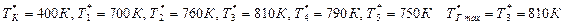
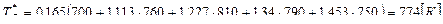 .
.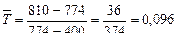 - приблізно10%, що знаходиться у межах рекомендованого допуску і говорить про досконалість даної камери згоряння.
- приблізно10%, що знаходиться у межах рекомендованого допуску і говорить про досконалість даної камери згоряння.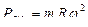
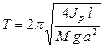 . Відкіля
. Відкіля 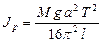 .
.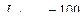 кг·м2, а
кг·м2, а  кг·м2, то похибка розрахункового методу буде:
кг·м2, то похибка розрахункового методу буде: 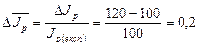 , або 20%, допустима похибка повинна бути не більше 5%. Таким чином точність розрахункового методу не достатня.
, або 20%, допустима похибка повинна бути не більше 5%. Таким чином точність розрахункового методу не достатня.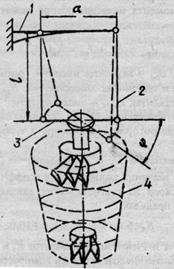
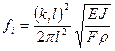 , [Гц] – власна частота коливань лопатки, де
, [Гц] – власна частота коливань лопатки, де 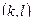 - характеризує спосіб закріплення лопатки та форму коливань лопатки.
- характеризує спосіб закріплення лопатки та форму коливань лопатки.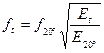 , де ft – власна частота згінних коливань лопатки при температурі t оС; f20 - власна частота згінних коливань лопатки при температурі 20 оС; Еt – модуль пружності матеріалу при t оС; Е20 - модуль пружності матеріалу при t оС.
, де ft – власна частота згінних коливань лопатки при температурі t оС; f20 - власна частота згінних коливань лопатки при температурі 20 оС; Еt – модуль пружності матеріалу при t оС; Е20 - модуль пружності матеріалу при t оС.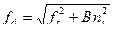 , де fd – власна частота коливань лопатки при її обертанні (динамічна власна частота); fс – власна частота нерухомої лопатки; В – коефіцієнт, що враховує геометричні розміри лопатки, форму коливань лопатки (визначається експериментально або за емпіричною залежністю); пs – частота обертання ротора у [об/с]. Приблизно В можна визначити за наступними емпіричними залежностями:
, де fd – власна частота коливань лопатки при її обертанні (динамічна власна частота); fс – власна частота нерухомої лопатки; В – коефіцієнт, що враховує геометричні розміри лопатки, форму коливань лопатки (визначається експериментально або за емпіричною залежністю); пs – частота обертання ротора у [об/с]. Приблизно В можна визначити за наступними емпіричними залежностями: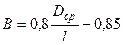 - для лопаток з постійним перетином профільної частини (пера лопатки);
- для лопаток з постійним перетином профільної частини (пера лопатки); 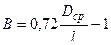 - для лопаток з перемінним перетином профільної частини;
- для лопаток з перемінним перетином профільної частини; 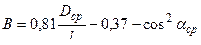 - для лопаток з закрученням профільної частини, де Dср – середній діаметр ротора; l – довжина пера лопатки; αср – середній кут закручення профільної частини лопатки.
- для лопаток з закрученням профільної частини, де Dср – середній діаметр ротора; l – довжина пера лопатки; αср – середній кут закручення профільної частини лопатки.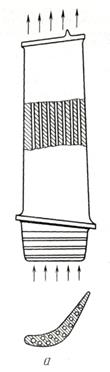
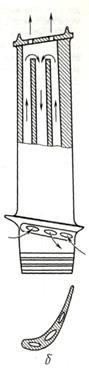
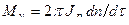 , де Jр – масовий полярний момент інерції ротора; п – оберти; τ – час запуску. Відкіля маємо час запуску в аналітичному вигляді:
, де Jр – масовий полярний момент інерції ротора; п – оберти; τ – час запуску. Відкіля маємо час запуску в аналітичному вигляді: 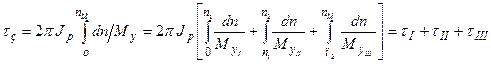 , де момент прискорення визначається, як алгебраїчна сума діючих складових моментів (М пу, М с , М т), а τІ, τІІ, τІІІ – час першого, другого, третього етапів запуску.
, де момент прискорення визначається, як алгебраїчна сума діючих складових моментів (М пу, М с , М т), а τІ, τІІ, τІІІ – час першого, другого, третього етапів запуску.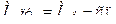 , де М о – початковий пусковий момент; с – коефіцієнт, що характеризує тип пускового пристрою. Слід мати на увазі, що для забезпечення оптимальної продовжності запуску М пу при частоті обертання п 1 повинен бути у 2…3 рази більшим моменту опору обертанню ротора М с. У власну чергу
, де М о – початковий пусковий момент; с – коефіцієнт, що характеризує тип пускового пристрою. Слід мати на увазі, що для забезпечення оптимальної продовжності запуску М пу при частоті обертання п 1 повинен бути у 2…3 рази більшим моменту опору обертанню ротора М с. У власну чергу  , де М к – момент, що потрібен для приводу компресора; а – коефіцієнт пропорційності, що визначається через параметри робочого процесу на режимі малого газу, тобто
, де М к – момент, що потрібен для приводу компресора; а – коефіцієнт пропорційності, що визначається через параметри робочого процесу на режимі малого газу, тобто 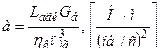 , Lад к – питома адіабатична робота компресора; Gв – секундна витрата повітря; ηк – ККД компресора; пмг – оберти ротора на малому газі. Момент на характеристика турбіни майже лінійна на І-му, ІІ-му та частково ІІІ-му етапах запуску. Відомо, що при п=п 1 М тІІ=0; при
, Lад к – питома адіабатична робота компресора; Gв – секундна витрата повітря; ηк – ККД компресора; пмг – оберти ротора на малому газі. Момент на характеристика турбіни майже лінійна на І-му, ІІ-му та частково ІІІ-му етапах запуску. Відомо, що при п=п 1 М тІІ=0; при  п=п р М тІІ= М сІІ; при
п=п р М тІІ= М сІІ; при 


