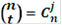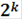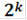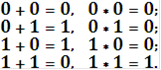Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения о системе scilabСодержание книги Поиск на нашем сайте
SciLab - пакет прикладных математических программ, предоставляющий мощное открытое окружение для инженерных (технических) и научных расчётов [2].
Возможности SciLab
Возможности SciLab содержит множество математических функций, и есть возможность добавления новых, написанных на различных языках (C, C++, Fortran …). В системе доступно множество инструментов: · 2D и 3D графики, анимация · Линейная алгебра, разреженные матрицы · Полиномиальные и рациональные функции · Интерполяция, аппроксимация · Симуляция: решение ОДУ и ДУ · Дифференциальные и не дифференциальные оптимизации · Обработка сигналов · Параллельная работа · Статистика · Работа с КА SciLab имеет схожий с MATLAB язык программирования. В состав пакета входит утилита, позволяющая конвертировать документы Matlab в SciLab. SciLab позволяет работать с элементарными и большим числом специальных функций (Бесселя, Неймана, интегральные функции). Также имеет мощные средства работы с матрицами, полиномами (в том числе и символьно), производить численные вычисления (например, численное интегрирование) и решение задач линейной алгебры, оптимизации и симуляции, мощные статистические функции, а также средство для построения и работы с графиками. Основы помехоустойчивого кодирования
Основные положения
Задача кодера источника - представить подлежащие передаче данные в максимально компактной и, по возможности, неискаженной форме. При передаче информации по каналу связи с помехами в принятых данных могут возникать ошибки. При большом числе ошибок полученной информацией пользоваться нельзя. Возможность использования кодирования для уменьшения числа ошибок в канале была теоретически показана К. Шенноном в 1948 году в его работе “Математическая теория связи”. В ней было сделано утверждение, что если скорость создания источником сообщений (производительность источника) не превосходит некоторой величины, называемой пропускной способностью канала, то при соответствующем кодировании и декодировании можно свести вероятность ошибки в канале к нулю. [3]. Вскоре, однако, стало ясно. Что фактическое ограничение на скорость передачи устанавливаются не пропускной способностью канала, а сложностью схем кодирования и декодирования. Поэтому усилия разработчиков и исследователей в последние десятилетия были направлены на поиски эффективных кодов. Создание практически реализуемых схем кодирования и декодирования, которые по своим характеристикам приближались бы к предсказанным теоретически.
Основные принципы
Кодирование с исправлением ошибок представляет собой метод обработки сообщений, предназначенный для повышения надежности при передачи по каналам связи. Хотя различные схемы кодирования очень не похожи друг на друга и основаны на различных математических теориях, всем присущи два общих свойства. Первое - использование избыточности. Закодированные последовательности всегда содержат дополнительные, или избыточные, символы. Количество символов в кодовой последовательности y всегда больше, чем необходимо для однозначного представления любого сообщения Второе - свойство усреднения, означающее, что избыточные символы зависят от нескольких информационных символов, то есть информация, содержащаяся в кодовой последовательность x, перераспределяется также и на избыточные символы. Существует два больших класса корректирующих кодов - блочные и сверточные. Определяющее различие между этими кодами состоит в отсутствии и наличии памяти кодера. Кодер для блочных кодов делит непрерывную информационную последовательность x на блоки - сообщений длиной k символов. Кодер канала преобразует блоки - сообщений x в более длинные двоичные последовательности y, состоящих из n символов и называемые кодовыми словами. Символы (n - k),добавляемые к каждому блоку - сообщению кодером, называются избыточными. Они не несут никакой дополнительной информации, и их функция состоит в обеспечении возможности обнаруживать (или исправлять) ошибки, возникающие в процессе передачи [3]. Для оценки потенциальных способностей кода можно воспользоваться пределом Хэмминга
где Заметим, что неравенство определяет минимальное необходимое число избыточных бит (нижнюю границу) для исправления всех комбинаций ошибок вплоть до t - битовых. Иначе можно сказать, что неравенство определяет верхнюю границу возможностей, когда в коррекции t - битовых ошибок как функцию числа бит чётности n - k.
Как мы ранее показали, k - разрядным двоичным словом можно представить Такое множество Термин “ без памяти ” означает, что каждый блок из n символов зависит только от соответствующего информационного блока из k символов и не зависит от других блоков. Линейные блочные коды
Для блочного кода с Одним из условий реализуемости блочных кодов является условие линейности. Кодовые символы в аддитивных блочных кодах в алгебраическом смысле образуют линейную аддитивную группу относительно операции суммированию по модулю 2. Работая с двоичными кодами, мы постоянно будем сталкиваться с элементами двоичной арифметики, поэтому определим основные понятия. Возьмем простейшее поле, состоящее из двух элементов - нуля " 0 " и единицы " 1 ". Определим для него операции сложения и умножения по модулю 2:
Желательным качеством линейных блочных кодов является систематичность. Аддитивный код имеет вид изображённый на рисунке 3.1, то есть содержит неизменную информационною часть длиной k символов и избыточную длиной n - k символов.
Рисунок 3.1
Блочный код, обладающий свойством линейности и систематичности, называется линейным блочным систематичным кодом ( n, k ) - кодом.
|
||||||
|
Последнее изменение этой страницы: 2020-03-27; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.73.198 (0.009 с.) |


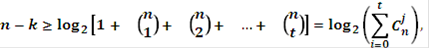
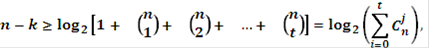 (3.1)
(3.1)