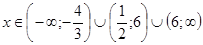Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування раціональних нерівностей вищих степенів узагальненним методом інтервалів
Нехай потрібно розв'язати нерівність
де
Для розв'язання нерівності
узагальненим методом інтервалів на числову вісь наносимо числа Зауваження 1. Якщо зустрічаються вирази Зауваження 2. Наведені вище міркування справедливі і для нерівностей виду
Приклад 1. Розв’язати нерівність
Перепишемо нерівність у рівносильному вигляді
Числа
на одному з інтервалів. Зокрема, взявши точку
-7 -
Відповідь:.
Приклад 2. Розв’язати нерівність
Числа
-3 1 5 x
Відповідь: Приклад 3. Розв’язати нерівність
Числа
-1 1 2 x
Відповідь: Приклад 4. Розв’язати нерівність
Числа
-3 -1 0 x
Відповідь:. Приклад 5. Розв’язати нерівність
Перепишемо нерівність
Числа
на одному з інтервалів. Зокрема, взявши точку
- Відповідь:.
|
|||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.158 (0.014 с.) |
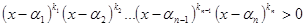 ,
, цілі додатні числа;
цілі додатні числа;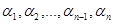 — дійсні числа, серед яких немає рівних і такі, що
— дійсні числа, серед яких немає рівних і такі, що  . Нерівності подібного типу розв'язують із застосуванням узагальненого метода інтервалів. В основі цього метода лежить така властивість двочлена
. Нерівності подібного типу розв'язують із застосуванням узагальненого метода інтервалів. В основі цього метода лежить така властивість двочлена  точка
точка  ділить числову вісь на дві частини, причому якщо
ділить числову вісь на дві частини, причому якщо 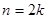 (
( - парне), то вираз
- парне), то вираз 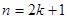 (
( додатний, а ліворуч від точки
додатний, а ліворуч від точки 
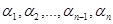 ; в проміжку праворуч від найбільшого з них ставимо знак «плюс», а потім, рухаючись справа наліво, при переході через чергове число
; в проміжку праворуч від найбільшого з них ставимо знак «плюс», а потім, рухаючись справа наліво, при переході через чергове число  змінюємо знак, якщо
змінюємо знак, якщо  — непарне число, і зберігаємо знак, якщо.
— непарне число, і зберігаємо знак, якщо.  , то праворуч від найбільшого з
, то праворуч від найбільшого з  не обов'язково буде знак «+». У цьому випадку найкраще визначити знак лівої частини нерівності в якомусь з інтервалів, а потім поставити знаки в кожному з інтервалів з урахуванням викладених вище міркувань.
не обов'язково буде знак «+». У цьому випадку найкраще визначити знак лівої частини нерівності в якомусь з інтервалів, а потім поставити знаки в кожному з інтервалів з урахуванням викладених вище міркувань. ,
,  ,
,  , де
, де .
.

 ,
,  ,
,  ,
,  є коренями рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції
є коренями рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції
 з інтервалу
з інтервалу  , дістаємо
, дістаємо  . Проводимо через задані точки «криву знаків» з урахуванням того, що ліворуч і праворуч точки
. Проводимо через задані точки «криву знаків» з урахуванням того, що ліворуч і праворуч точки  показник степеня (число 4) є числом парним.
показник степеня (число 4) є числом парним.






 +
+ 

 6 x
6 x

 ,
,  ,
,  є коренями рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції
є коренями рівняння. Наносимо ці числа на числову вісь і визначаємо знак лівої частини функції  на одному з інтервалів. Зокрема, взявши точку
на одному з інтервалів. Зокрема, взявши точку  , дістаємо
, дістаємо  . Провівши «криву знаків» з урахуванням того, що ліворуч і праворуч точки
. Провівши «криву знаків» з урахуванням того, що ліворуч і праворуч точки  і
і  буде той самий знак «-», тому що у виразах
буде той самий знак «-», тому що у виразах  і (х + 3)6
і (х + 3)6  показник степеня (число 4 і 6 відповідно) є парні числа, визначаємо знак f(x) в кожному з інтервалів.
показник степеня (число 4 і 6 відповідно) є парні числа, визначаємо знак f(x) в кожному з інтервалів.





 .
.
 ,
,  ,
,  х2
х2  , то
, то  для всіх
для всіх 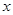 і, значить, парабола
і, значить, парабола 

 .
.
 ,
,  на одному з інтервалів. Зокрема, взявши точку
на одному з інтервалів. Зокрема, взявши точку  , дістаємо
, дістаємо  . Проводимо через задані точки «криву знаків» і дістаємо розв’язання.
. Проводимо через задані точки «криву знаків» і дістаємо розв’язання.
 .
. .
. .
. ,
,  ,
,  є коренями рівняння Наносимо дані точки на числову вісь і визначаємо знак лівої частини функції
є коренями рівняння Наносимо дані точки на числову вісь і визначаємо знак лівої частини функції
 , дістаємо
, дістаємо  . Проводимо через задані точки «криву знаків» і дістаємо розв’язання.
. Проводимо через задані точки «криву знаків» і дістаємо розв’язання.



 6 x
6 x