Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Запись алгоритма обмена значениями двух переменных, перестановки элементов вектора и матрицы. Запись алгоритма в известных вам формах.Содержание книги
Поиск на нашем сайте
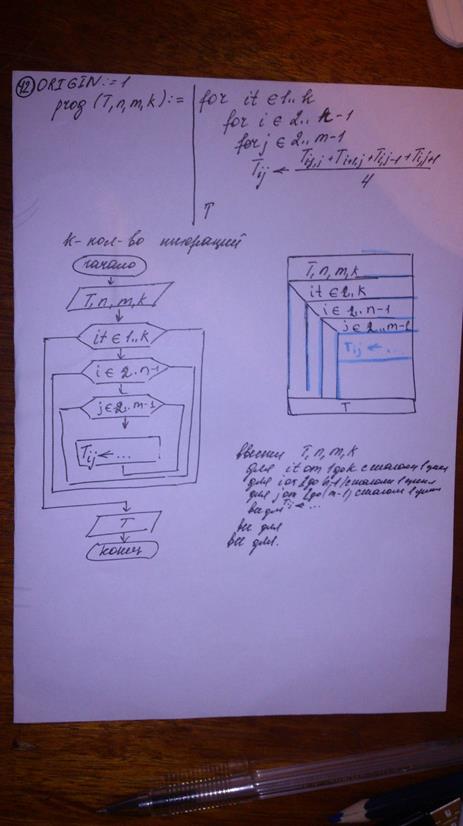
для записи перестановки 2х значений (A, B) нужно воспользоватся следующим алгортмом: 1) взять некую перемену (С)и пресвоить ей некоторое из значений (к примеру A) C:=A 2)к значению A присваиваем значение B A:=B 3) к значению B присвоить значение С B:=C В сфере mathcad это програма будет выглядить так: prog (A, B):=| C:=A | A:=B |B:=C |(A, B) 41. Метод итераций на примере расчета температурного поля.
Метод итерации основан на постепеном пересчете ячеек которыевнутри В mathcad эта запис будет выглядеть так:
42. Алгоритм метода итераций на примере расчета температурного поля. Запись алгоритма в известных вам формах.
43. Постановка задачи метода итераций на примере расчета температурного поля.
Двумерные массивы. Алгоритмы накопления для массива в целом и по строкам и столбцам. Запись алгоритма в известных вам формах. Двумерный массив - это одномерный массив, элементами которого являются одномерные массивы. Другими словами, это набор однотипных данных, имеющий общее имя, доступ к элементам которого осуществляется по двум индексам. Наглядно двумерный массив удобно представлять в виде таблицы, в которой n строк и m столбцов, а под ячейкой таблицы, стоящей в i-й строке и j-м столбце понимают некоторый элемент массива a[i][j]. Действительно, если разобраться с тем, что такое a[i] при фиксированном значении i, то увидим, что это одномерный массив, состоящий из m элементов, к которым можно обращаться по индексу: a[i][1], a[i][2],..., a[i][m]. Схематически это вся i-я строка строка таблицы. Аналогично, если мы рассмотрим одномерный массив строк, то сможем заметить, что это так же двумерный массив, где каждый отдельный элемент - это символ типа char, а a[i] - это одномерный массив, представляющий отдельную строку исходного одномерного массива строк. По-другому двумерный массив также называют матрицей, а в том случае, когда n=m (число строк равно числу столбцов) матрицу называют квадратной.
Прием накопления суммы Данный алгоритмический прием используется, когда надо просуммировать большое количество чисел. Для этого переменной, в которую будет записываться сумма, в начале присваивается нулевое значение, затем делается цикл, где на каждом шаге к этой переменной добавляется очередное число.
Очень важная, фундаментальная идея, использованная в данном приеме, состоит в том, что результат выполнения каждого шага цикла, зависит от значения переменной, вычисленной на предыдущем шаге. Таким образом, вместо тривиального повторения одного и того же, мы на каждом шаге получаем новый результат. Так в приведенном примере очередное число добавляется к значению переменной s, полученному на предыдущем шаге. А к чему добавляется очередное число на самом первом шаге? Чтобы было к чему добавлять, перед циклом обязательно должна присутствовать инициализация (присваивание начального значения) переменной, в которой накапливается сумма. Чаще всего требуется присвоить ей начальное значение 0. 45. Двумерные массивы. Алгоритмы нахождения экстремальных элементов и их местоположения для массива в целом, по строкам и столбцам. Запись алгоритма в известных вам формах Работа с диагональными элементами квадратных матриц. Примеры.
|
||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.44.252 (0.008 с.) |

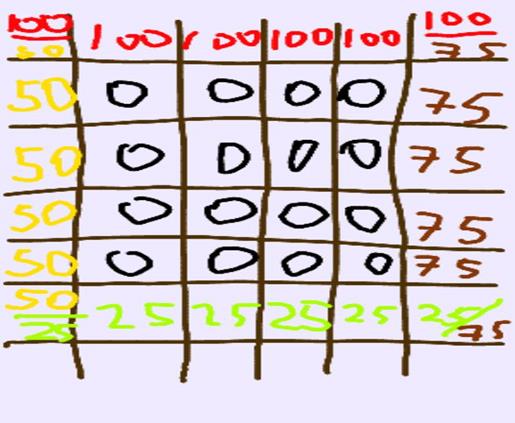 Ну какбы, блять, берем температурное поле на гранях этого поля заданы температуры. Поле состоит из точек че больше точек тем точнее результат. Температура каждой точки определяется средним арифметиким температур точек вокруг данной. температурное поле сравнивают с матрицей MxN. В начальный момент температурное поле будет выглядеть так,какбы по границам поля будут заданые нам температуры (100, 300, 25 градусов). а в центре будут нули
Ну какбы, блять, берем температурное поле на гранях этого поля заданы температуры. Поле состоит из точек че больше точек тем точнее результат. Температура каждой точки определяется средним арифметиким температур точек вокруг данной. температурное поле сравнивают с матрицей MxN. В начальный момент температурное поле будет выглядеть так,какбы по границам поля будут заданые нам температуры (100, 300, 25 градусов). а в центре будут нули