
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В результате получаем уравнение узловых напряжений в форме баланса токов в матричном виде для общего случая, когда в схеме замещения имеются и источники тока и источники эдс.
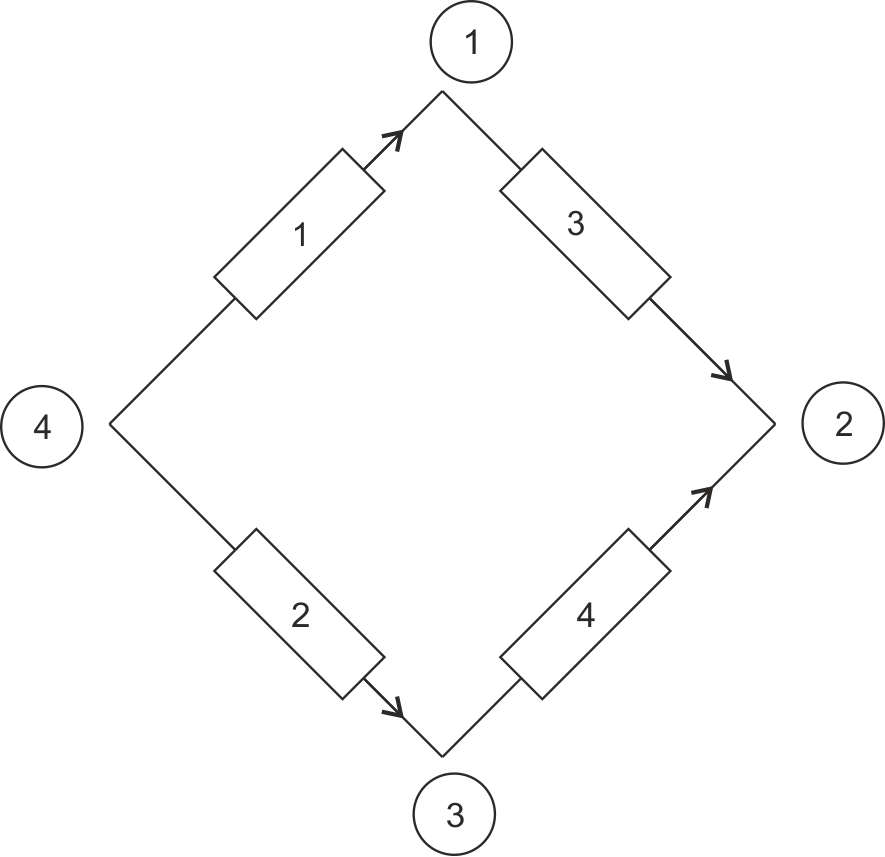
Рассчитаем элементы матрицы узловых проводимостей для схемы замещения, приведенной на рис. 1.4
При совпадении базисного и балансирующего узлов матрица узловых проводимостей 1. Это матрица симметрична относительно главной диагонали, т.е.
2. Матрица На главной диагонали этой матрицы, т.е. на пересечении строк и столбцов, относящихся к одним и тем же узлам, стоят элементы При несовпадении базисного и балансирующего узлов, матрица узловых проводимостей В связи с этим целесообразно совмещать базисный и балансирующий узел во всех случаях, когда это не противоречит классической постановке задачи расчета установившегося режима электрической системы. Матричное уравнение Частные случаи записи узловых уравнений: 3. В схеме замещения отсутствуют задающие токи (I=0). Такая схема замещения используется для расчета токов короткого замыкания (КЗ) или электромеханических переходных процессов. В качестве базисного, совпадающего с балансирующим берется узел земли (нейтрали). При этом Тогда уравнения узловых напряжений (1) превратится в линейное и приобретет вид:
Возникновение трехфазного короткого замыкания в каком-то из узлов определяется тем, что в матрице узловых проводимостей исключается строка и столбец, соответствующие этому узлу. Одновременно исключается соответствующая строка из матрицы-столбца правых частей. После решения системы узловых уравнений (как правило, методом Гаусса) рассчитывают токи в ветвях
В промышленных программах расчетов токов КЗ иногда используют наложение аварийного режима на нормальный предшествующий режим.
· Второй частный случай: узловое уравнение в форме баланса токов записывается для схемы замещения, в которой отсутствуют ЭДС в ветвях(
Матричное уравнение узловых напряжений в форме балансирующих токов имеет:
4 узел – базисный и балансирующий
-матричное уравнение узловых напряжений в форме баланса токов для условий, когда ЭДС ветвей Это матричное уравнение нелинейно, т.к. для к-го узла
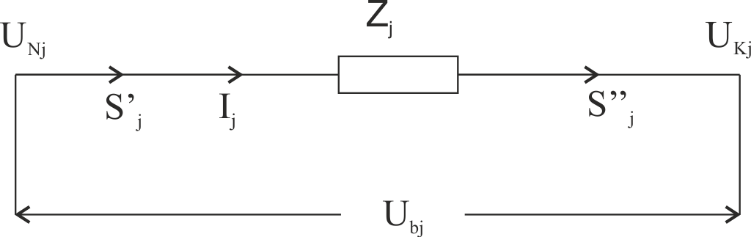
Здесь имеет место нелинейность вида Алгоритм расчета установившегося режима методом узловых напряжений 1. Формируется узловое уравнение в матричном виде (основная трудность – рассчитать элементы матрицы 2. Решается система узловых уравнений, так как оно нелинейно, то: · Или численным методом решения систем нелинейных алгебраических уравнений · Или линеаризуется (внешняя итерация) и несколько раз решается система линейных алгебраических уравнений. В результате находятся напряжения в узлах (с наперед заданной точностью). 3. Рассчитывают токи ветвей
4. Рассчитываются мощности в начале и в конце каждой ветви
и потери мощности в ветвях: суммарные: Общие правила формирования нелинейных узловых уравнений установившегося режима электрической системы при задании мощности узлов такие: 1. Один из генераторных(активных), как правило соответствующей мощной электростанции принимается в качестве балансирующего, совпадающего с базисным. 2. Поперечные ветви схемы замещения учитываются только в диагональных элементах матрицы узловых проводимостей
Полученные системы уравнений нелинейные, и, следовательно, могут быть решены только итерационно. Вопросы существования и единственности решения уравнений установившегося режима мы не рассматриваем, но можем утверждать, что согласно опыту практических расчетов для нормального режима электрической системы существует, как правило, одно технически допустимое решение. Преобразование системы уравнений узловых напряжений с комплексными коэффициентами и неизвестными к системе с действительными коэффициентами и неизвестными.
При расчетах на ПК система n уравнений узловых напряжений с комплексными коэффициентами и неизвестными часто приводится к системе 2n действительных уравнений порядка 2n с действительными неизвестными и коэффициентами, поскольку обработка комплексных чисел арифметическим условием компьютеров неэффективна (по времени). Матрица узловых проводимостей записывается в виде:
Подставляем указанные величины в уравнение узловых напряжений для второго частного случая. Подобные преобразования представляют самостоятельный интерес, т.к. обработка комплексных чисел арифметическими устройствами ПК осуществляется неэффективно. В матрице узловых проводимостей При решении на ПК система n уравнений узловых напряжений с комплексными коэффициентами и неизвестными часто приводится к системе действительных уравнений порядка 2 n, где n – число независимых узлов.
Подставляем указанные матрицы в уравнение узловых напряжений
Приравниваем отдельно действительные и мнимые части:
Эту систему можно записать в матричной форме (вспомнив о сумме клеточных матриц):
Поскольку диагональные элементы матрицы
Это построение матрицы удобно с точки зрения решения полученных уравнений итерационными методами, если диагональные элементы при неизвестных значениях напряжений больше всех остальных элементов в строке. В заключение еще раз отмечаем, что метод узловых напряжений используется в большинстве программ для расчетах установившихся режимов.
|
||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.120.103 (0.009 с.) |


 обладает следующими свойствами:
обладает следующими свойствами:
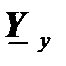 может быть легко сформирована непосредственно по схеме замещения (без перемножения матриц
может быть легко сформирована непосредственно по схеме замещения (без перемножения матриц  ):
):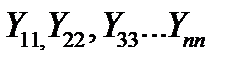 , равные суммам проводимостей ветвей, связанных с этими узлами (
, равные суммам проводимостей ветвей, связанных с этими узлами ( ). Остальные элементы этой матрицы, находящиеся на пересечении i - й строки и j – го столбца, равны взятым со знаком «минус» проводимостям ветвей между узлами i и j схемы замещения.
). Остальные элементы этой матрицы, находящиеся на пересечении i - й строки и j – го столбца, равны взятым со знаком «минус» проводимостям ветвей между узлами i и j схемы замещения. оказывается несимметричной, и на её главной диагонали могут находиться нулевые элементы. Это приводит к тому, что с точки зрения организации вычислений с применением ПК узловые уравнения оказываются менее рациональными.
оказывается несимметричной, и на её главной диагонали могут находиться нулевые элементы. Это приводит к тому, что с точки зрения организации вычислений с применением ПК узловые уравнения оказываются менее рациональными. нелинейно поскольку здесь
нелинейно поскольку здесь  - матрица- столбец нелинейных источников тока.
- матрица- столбец нелинейных источников тока.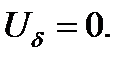
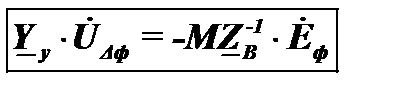
 .
. ).
).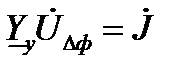






 - число.
- число. -номера независимых узлов
-номера независимых узлов , x – неизвестные напряжения в узлах.
, x – неизвестные напряжения в узлах.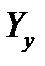 )
)

 -нагрузочные потери
-нагрузочные потери -есть еще поперечные потери холостого хода трансформаторов и потери активной мощности на корону.
-есть еще поперечные потери холостого хода трансформаторов и потери активной мощности на корону.
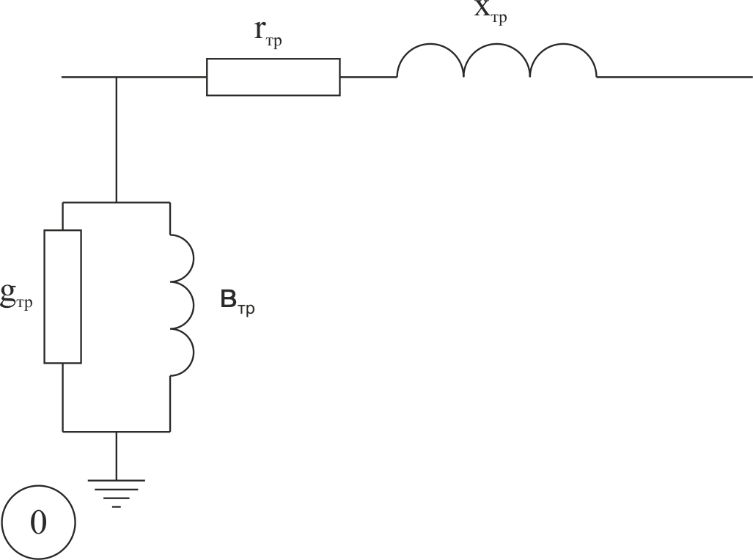
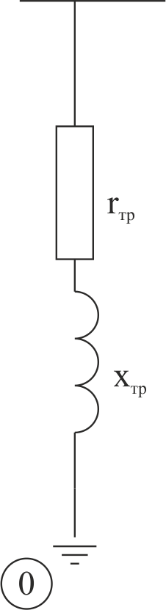

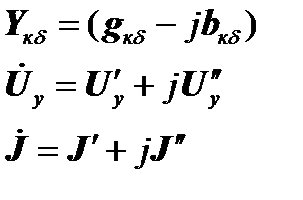 -в прямоугольной системе координат
-в прямоугольной системе координат , имеющей порядок
, имеющей порядок  , очень большое число нулевых элементов.
, очень большое число нулевых элементов.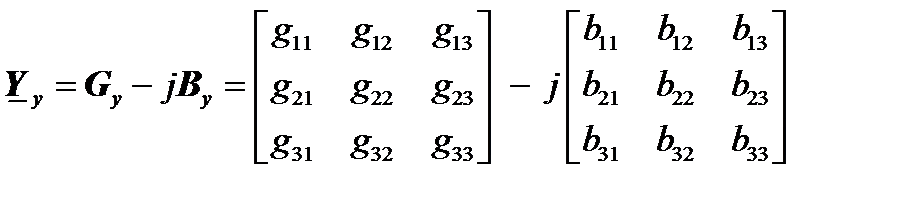 ,
, 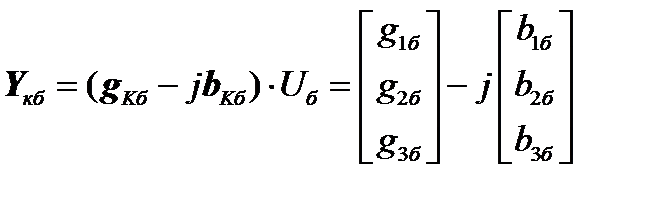
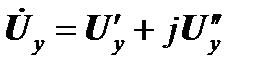 ,
,  .
.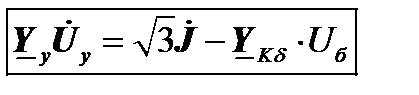



 обычно больше соответствующих элементов матрицы
обычно больше соответствующих элементов матрицы  по условиям улучшения вычислительной устойчивости при решении уравнений запишем эту систему уравнений иначе, изменив коэффициентов следующим образом:
по условиям улучшения вычислительной устойчивости при решении уравнений запишем эту систему уравнений иначе, изменив коэффициентов следующим образом:



