
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрические свойства векторного произведения
Теорема 13 1. Площадь параллелограмма, построенного на векторах
2. Доказательство: 1) Построим параллелограмм на векторах
2) Необходимость.
Достаточность. Алгебраические свойства векторного произведения 1. 2. 3. 4. 5. Доказательство свойств: 1.
По лемме №3
2. Докажем, что модули равны
Докажем, что вектора сонаправлены:
Тогда по лемме 3:
Тогда по лемме №3:
3. Доказать самостоятельно.
4.
Тогда по лемме №3:
5.
Повернём параллелограмм в плоскости
6. (Из свойства 1)
Векторное произведение в координатах Теорема 14 Пусть в ПДСК заданы векторы
Доказательство:
Рассмотрим
Причем Значит Аналогично доказывается, что В силу антикоммутативности векторного произведения
В силу свойства 3 векторного произведения
Мы доказали следующую таблицу.
Таблица векторных произведений
Используя свойства векторного произведения (дистрибутивность, ассоциативность умножения вектора на число) и таблицу векторных произведений вычислим
Следствие
Применение векторного произведения
Пусть даны в ПДСК вектора
В случае плоскости:
Векторное произведение в АСК
O
Смешанное произведение векторов Определение №44 Смешанным произведением векторов
Геометрический смысл смешанного произведения Теорема 15 Смешанное произведение некомпланарных векторов Смешанное произведение векторов Доказательство: 1) Рассмотрим вектора
Если Если 2)
♥ Замечание В формулировке теоремы предполагается, что базис правый; если ориентация базиса может быть любой, то соответствующие слова заменяем на взятого со знаком «+», если ориентация базиса и тройки совпадают, и со знаком «-», если ориентация тройки и базиса различны.
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.142.93 (0.009 с.) |
 , приведённых к общему началу, равна модулю их векторного произведения.
, приведённых к общему началу, равна модулю их векторного произведения.

 и
и 
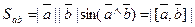
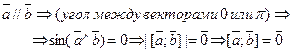

 – антикоммутативность
– антикоммутативность – ассоциативность относительно умножения на число
– ассоциативность относительно умножения на число
 , где
, где  – векторная проекция
– векторная проекция  на прямую перпендикулярную
на прямую перпендикулярную  и лежащую в плоскости векторов
и лежащую в плоскости векторов 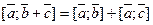 – дистрибутивность
– дистрибутивность
 - правая тройка (по определению)
- правая тройка (по определению) - левая тройка (по определению)
- левая тройка (по определению) - левая тройка (по лемме)
- левая тройка (по лемме)

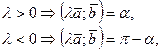


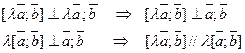
 - правая тройка
- правая тройка - правая тройка,
- правая тройка,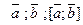 - правая тройка,
- правая тройка, - правая тройка, т.к.
- правая тройка, т.к. 

 - правая тройка
- правая тройка
 - левая тройка,
- левая тройка,

 - правая тройка
- правая тройка - правая тройка
- правая тройка























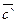


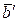

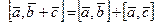

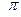 на
на  ; если смотреть из конца вектора
; если смотреть из конца вектора  , то против часовой стрелки. Каждый вектор умножаем на
, то против часовой стрелки. Каждый вектор умножаем на  .
.
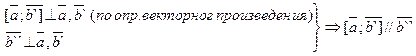
 - правая тройка (по определению)
- правая тройка (по определению) В силу того, что
В силу того, что 

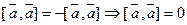
 . Тогда:
. Тогда:

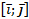 . Докажем, что
. Докажем, что  .
.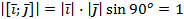 , а
, а  Длины векторов равны.
Длины векторов равны. (по определению векторного произведения), а
(по определению векторного произведения), а  (так как базисные векторы в ПДСК)
(так как базисные векторы в ПДСК) 
 .
. – правая тройка векторов и
– правая тройка векторов и  – правая тройка векторов (по определению). По Лемме №3
– правая тройка векторов (по определению). По Лемме №3  .
. ,
,  .
. ;
;  ;
;  .
. .
.


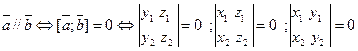


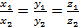 пропорциональность соответствующих координат.
пропорциональность соответствующих координат.

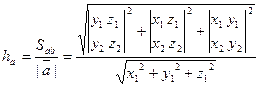


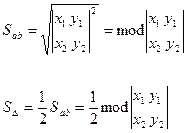
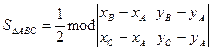 где
где 




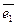
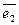



 называется скалярное произведение векторного произведения векторов
называется скалярное произведение векторного произведения векторов  на вектор
на вектор  .
.
 равно объёму параллелепипеда, построенного на этих векторах, приведенных к общему началу, взятому со знаком «+», если тройка векторов
равно объёму параллелепипеда, построенного на этих векторах, приведенных к общему началу, взятому со знаком «+», если тройка векторов  ,
,  и единичный вектор
и единичный вектор  . Тогда
. Тогда  – правая тройка (так как
– правая тройка (так как  по определению).
по определению).
 – правая тройка, то
– правая тройка, то  (вектор
(вектор  направлен в то же полупространство, что и
направлен в то же полупространство, что и  , относительно плоскости
, относительно плоскости 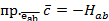 (вектора
(вектора  .
. векторы компланарны.
векторы компланарны.


