
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Информационный процесс представления знаний.Содержание книги
Поиск на нашем сайте
Тема 1. Информационный процесс представления знаний. 1.1 Основные понятия дисциплины. Существует особый класс систем, решающих задачи, связанные с интеллектуальной деятельностью человека. Такие системы имитируют процессы, протекающие в человеческом мозге при решении трудно формализуемых задач принятия решений в условиях неполной и противоречивой информации, а также процессы, моделирующие поведение биологических объектов в живой природе. Такие системы называются интеллектуальными. Основной компонент интеллектуальных систем (ИС), отличающий их от других систем принятия решений, является база знаний (БЗ), хранящая информацию о предметной области в виде различных моделей описания высокоструктурированный взаимосвязанных данных, сохраняющих семантику предметной области. Проблема построения БЗ, выбора модели представления знаний внутри нее, а также извлечения знаний из первичных источников (человек-эксперт) – основная проблема при разработке систем, основанных на знаниях (Knowledge-based system). Знания – специальная форма представления информации (высшая форма, метаинформация), позволяющая человеческому мозгу накапливать, хранить, понимать и воспроизводить информацию. Знания в технических системах фиксируются в виде описаний на некотором языке (язык представления знаний), сохраняющем связи между данными, описывающими задачу, с учетом синтаксиса, семантики и прагматики. Знания характеризуются пятью свойствами: 1) Внутренняя интерпретируемость – связь элементов данных с некоторой системой имен, позволяющей знать, что хранится в памяти, и уметь отвечать на вопросы о содержании памяти. 2) Рекурсивная структурируемость – элементы данных могут разбиваться на более мелкие или группироваться в более крупные структуры (классы), описывающие все возможные проявления отношений между объектами предметной области. 3) Взаимосвязь единиц элементов данных – сопоставление в памяти системы некоторой структуры отношений между объектами предметной области. 4) Наличие семантического пространства (поля знаний) с присущей метрикой. Оно характеризует взаимное положение элементов данных с точки зрения смысла. 5) Активность. В традиционном программировании данные – пассивные элементы, а активные действия выполняют процедуры и функции. В ИС данные – активные элементы, т.е. они побуждают к определенным действиям, изменяют структуру взаимосвязей. Знания существуют в следующих формах: ü в памяти человека-эксперта как результат мышления; ü на материальных носителях (учебники, пособия и т.д.); ü в виде поля знаний – условного описания основных объектов предметной области, их атрибутов, закономерностей и связей (данное описание слабо формализовано); ü в виде описаний на некотором языке представления знаний, т.е. языке сверхвысокого уровня (продукционные, логические языки, семантические сети, фреймы и др.); ü в БЗ – на внешних носителях информации или внутри системы.
Классификация знаний. Существуют различные критерии классификации знаний. Различают знания: ü декларативные и процедурные; ü глубинные и поверхностные; ü жесткие и мягкие; ü теоретические и эмпирические. I группа. 1) Исторически первыми появились процедурные знания. Это – знания, растворенные в алгоритмах решения задач. Такие знания управляют данными. Чтобы изменить процесс управления нужно изменить программу или алгоритм. 2) Декларативные знания описывают состояние предметной области в виде таблиц, списков и абстрактных структур данных, а также логических правил, задающих взаимосвязи и отношения между ними. Декларативные знания представляются на некотором языке, приближенном к естественному языку человека. II группа. 1) Глубинные знания – это абстракции, аналогии, схемы, полученные в результате обобщения понятий предметной области и протекающих в ней процессов. Они объясняют явления и используются для прогнозирования поведения объектов. 2) Поверхностные знания – это совокупность эмпирических ассоциаций между отдельными событиями и фактами предметной области. Большинство современных ИС работают с поверхностными знаниями. Это связано с отсутствием универсального метода извлечения и выявления глубинных структур знаний человека. III группа. 1) Жесткие знания используют ограниченные типы данных и не допускают множественной трактовки. 2) Мягкие знания допускают множественные, расплывчатые описания и приводят к нечетким алгоритмам поиска решения. Знания человека – мягкие знания. IV группа. 1) Теоретические знания формируются согласно строгим формальным описаниям предметной области. 2) Эмпирические знания кроме этого учитывают личный опыт эксперта при решении конкретной задачи.
Существует несколько базовых моделей представления знаний в БЗ ИС: 1. Формальная логическая модель, которая использует теорию исчисления предикатов первого порядка, представленных в «клаузальной» форме (от англ. clause – пункт, статья). 2. Продукционная модель, использующая представление знаний в виде правил по форме: Если (условие) то (действие). 3. Модель на основе семантической сети, в которой знания представляются в виде графа, узлы которого – факты, явления предметной области, а дуги – отношения между ними. 4. Модель на основе фреймов – это некоторая абстрактная пустая структура, характеризующая какое-либо понятие. Фрейм имеет имя и слоты.
Тема 2. Пример 2.1 Пусть в БЗ содержатся следующие знания о предметной области «Биржа»: 1) База фактов: F1. Уровень цен на бирже падает. F2. Уровень цен на бирже растет. F3. Процентные ставки падают. F4. Процентные ставки растут. F5. Курс доллара растет. F6. Курс доллара падает. 2) База правил: R1. Если F3, то F2. R2. Если F4, то F1. R3. Если F6, то F4. R4. Если F5, то F3. 3) Запрос к БЗ: Как изменится ситуация на бирже в случае падения курса доллара? 0. F6 = true 1. R3 ® F4 = true 2. F4 = true 3. R2 ® F1 = true 4. F1 = true 5. Result: F6 ® F4, F1
Примечания: 1) При использовании продукционной модели возникает проблема контроля непротиворечивых данных в БЗ (ответственность возлагается на программиста). 2) Изменение предметной области приводит к появлению новых фактов о ее состоянии, отсутствующих в БЗ. Это позволяет автоматически пополнять БЗ, укоряя процесс поиска. Например, в результате запроса появляется новое правило: R5. Если F6, то F4& F1, которое позволяет убрать правило R3 из базы правил. 3) Найденные в соответствии с запросом решения и цепочки вывода помещаются в базу типовых решений, что позволяет при повторном решении той же задачи использовать готовые шаблоны. 4) При добавлении пользователем или экспертом новых фактов и правил о предметной области нужно вначале проверить их достоверность перед помещением в БЗ.
Продукционная модель наиболее часто применяется в промышленных экспертных системах, т.к. она проста, понятна, модифицируема. Разработаны специальные языки представления знаний с помощью продукционной модели – OPS5, G2. на базе данной модели строятся экспертные системы, такие как EXSYS, ЭКО. Фреймы. Термин фрейм (от англ. frame – рамка, каркас) был предложен Маренном Минским в 70-е годы для обозначения структуры знаний для восприятия пространственных сцен. Фрейм — это абстрактная модель для представления какой-либо сцены. Модель на основе фреймов легко программировать, использую объектную технологию. Основная сложность использования этой модели заключается в разработке алгоритмов поиска на множестве фреймов. Пример 2.2. Фрейм «комната» описывает шаблон помещения с четырьмя стенами, полом, потолком, окнами и дверью некоторой площадью. Конкретные значения их не определены. Каждый составляющий – это слот. Слот представляет собой незаполненное значение некоторого атрибута. Различают несколько типов фреймов: ü фреймы-образы; ü фреймы-структуры (заем, залог, вексель); ü фреймы-роли (менеджер, кассир, клиент); ü фреймы-сценарии (банкротство, собрание акционеров, празднование именин); ü фреймы-ситуации (тревога, авария, рабочий режим устройства) и др. Традиционно структура фрейма может быть представлена как список свойств: Имя фрейма: роль 1 (слот 1); роль 2 (слот 2); … роль k (слот k); Здесь: Имя слота: (признак 1, значение 1), (признак 2, значение 2), … (признак N, значение N). Связь В данном случае связь определяет отношение между фреймами.
Существует несколько способов получения знаний слотами фреймов: 1) По умолчанию от фрейма-образа. 2) Через наследование свойств от фрейма, указанного в слоте АКО (АКО = A-Kind-Of). 3) Путем вычисления значения по формуле, указанной напрямую в слоте. 4) Через присоединенную процедуру. 5) Из диалога с пользователем. Важнейшим свойством теории фреймов является наследование свойств по АКО-связям. Слот АКО при этом указывает на фрейм более высокого уровня иерархии, от которого наследуются значения одноименных слотов. Пример 2.3. 1) Человек: АКО = млекопитающее; Умеет = мыслить. 2) Ребенок: АКО = человек; Возраст = 0 – 16 лет; Рост = 50 – 180 см; Любит = сладкое. 3) Ученик: АКО = ребенок; Учится = в школе, в ПТУ; Возраст = 7 – 17 лет. В данной сети фреймов на вопрос: «Любят ли ученики сладкое?» - получает ответ «Да».
Для фреймовой модели разработаны специальные языки программирования, наиболее известные из которых FRL и KRL. На их основе построены такие экспертные системы, как ANALYST, TRISTAN.
Семантические сети Семантическая сеть — это ориентированный граф, вершины которого — понятия, а дуги — отношения между ними. Понятия – это объекты, свойства объектов, процессы и др. Отношения — это семантические связи между понятиями. Существует 4 базовых типа отношений: 1 – класс – элемент класса (цветок — роза); 2 – свойство – значение (цвет — желтый); 3 – пример элемента класса (роза — чайная); 4 – целое – часть (роза — лепесток). По количеству отношений различают семантические сети: 1) Однородные (с единственным типом отношений). 2) Неоднородные (с различными типами отношений). По числу связей различают семантические сети: 1 – бинарные (в которых отношения связывают два объекта); 2 – n-арные (в которых есть специальные отношения, связывающие более двух понятий). Пример 2.4. 1) Иванов является директором.
2) «Альфа-банк» имеет гарантии платежеспособности клиента и размещается в г. Москва.
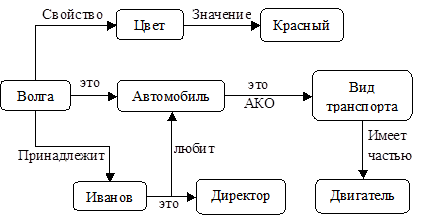
3) В общем случае для описания даже простой модели предметной области получается сложная семантическая сеть:
4) Для анализа множества ситуаций, возникающих в предметной области, используют обобщения семантических сетей, вводя подсети, соответствующие роли или ситуации предметной области. 1. «Альфа-банк» предоставил кредит Радиозаводу. 2. «Альфа-банк» получил кредит от МВФ. При обобщении здесь вводят 2 типа ролей: - кредитор; - заемщик, - и строят подсеть:
Эта модель наиболее близко описывает представления о памяти человека (нейронные сети). Ее недостаток – сложность процедуры поиска и громоздкая структура сети. Существуют языки представления знаний в виде семантических сетей, из которых известны Net, SIMER, на их основе строятся экспертные системы CASNET, TORUS. Пример 2.5 1) Унарный предикат: директор(Иванов) 2) Бинарный предикат: является(Иванов, директор)
В общем случае n-арный предикат: роль1(имя1, значение1)Ç роль2(имя2, значение2)Ç … Çроль n(имя n, значение n) такой предикат принимает значение true в случае истинности всех его составляющих. Пример 2.6 Продавцом товара является фирма «Компьютер и офис», покупателем товара является Иванов, вид товара – компьютер. 1) продавец(Компьютер и офис) Ç покупатель(Иванов) Ç товар(ПК) 2) продавец(товар, Компьютер и офис) Ç покупатель(Иванов) Ç товар(ПК)
Для записи правил в логической модели используется специальная форма представления правил – клаузальная форма. заключение:– условие1, условие2 Если истинны все условия, то истинно заключение. Пример 2.7 Если «Альфа-банк» имеет гарантии платежеспособности клиента, и эти гарантии принимаются для предоставления кредита, то он предоставляет кредит. Введем: А – имеет. В – использует. С – предоставляет. Получаем: С(Альфа-банк, решение о кредите):– А(Альфа-банк, гарантии), В(гарантии, решение о кредите).
Для предания общности в правилах вместо констант в качестве параметров предикатов используют переменные. Например: C(X,Y):– A(X,Z), B(Z,Y).. БЗ с использованием логической модели состоит из множества фактов и правил, описывающих предметную область. Основным языком, использующим эту модель, является язык программирования Пролог. Пример 2.8 Том, Майкл и Джон являются членами Альпинклуба. Каждый из них является или горнолыжником, или скалолазом, или и ем и другим. Никто из скалолазов не любит дождь. Все горнолыжники любят снег. Майкл любит все то, что не любит Том. Майкл не любит то, что любит Том. Джон любит снег. Том любит снег и дождь. Вопрос: Кто есть кто? Анализируя исходные данные, можно сделать следующие выводы: Том является только горнолыжником. Майкл не горнолыжник, а скалолаз. Джон – горнолыжник. Domains Name = tom, mikle, john. Weather = rain, snow. Spec = sk, gor. Predicates club(Name). like(Name, Weather). nolike(Name, Weather). is(Name, Spec). question clauses club(tom). club(mikle). club(john). like(tom, snow). like(tom, rain). like(john, snow). like(mikle, X):- not(like(tom, X)). nolike(X, Y):- not(like(X, Y)). nolike(mikle, Y):- like(tom, Y). is(X, gor):- club(X), like(X, snow). is(X, sk):- club(X), nolike(X, rain). question:- nl, is(Name, sk), not(is(Name, gor)), write(“Только скалолаз”, Name), nl, fail. question:- nl, is(Name, gor), not(is(Name, sk)), write(“Только горнолыжник”, Name), nl, fail. question:- nl, is(Name, sk), is(Name, gor), write(“Горнолыжник и скалолаз”, Name), nl, fail. question:- nl, is(tom, Spec), write(“Том -”, Spec), nl, fail. question:- nl, write(“Стоп”). goal question.
Тема 3. Язык Пролог. Пример 3.1 Predicates % ax2 + bx + c = 0 zapros % цель povtor % рекурсия kvur(real, real, real) clauses kvur(A, B, C):– B*B–4*A*C>0, X1 = (-B+sqrt(B*B–4*A*C))/2/A, X2 = (-B-sqrt(B*B–4*A*C))/2/A, write(“X1=”, X1), write(“X2=”, X2), nl. kvur(A, B, C):– B*B–4*A*C=0, X = (-B)/(2*B), write(“X=”, X), nl. kvur(A, B, C):– B*B–4*A*C<0, write(“No Solutions”). zapros:– write(“Input A, B, C”), povtor, write(“A=”), Readreal(A), A<>0, nl, write(“B=”), Readreal(B), nl, write(“C=”), Readreal(C), nl, kvur(A, B, C), write(“Press Q for Exit”), nl, Readchar(S), S=’Q’,!. povtor. povtor:– povtor. goals makewindow(1, 15, 1, “ax2 + bx + c = 0”, 0, 0, 25, 80), zapros.
Известно, что рекурсия в большинстве случаев порождает алгоритмы с экспоненциальной сложностью. Однако Пролог компилирует рекурсию в оптимизационную итерационную петлю. Это означает, что хотя программная логика представлена рекурсивно, скомпилированный код так же эффективен, как и программа, написанная на обычных языках с использованием простых циклов. Пример 3.2 Распечатка фактов из базы фактов. Predicates country(symbol). print. clauses % база фактов country(“England”). country(“Russia). … print:- country(X), write(X), nl, fail. print. goal print.
Пример 3.3 Найти сумму чисел ряда 0.. N.
S = 0 for i = 1 to N do S = S + i; write(S)
S = 0, i = 1 while i<=N do begin S = S + i; i = i + 1; end; write(S). Predicates summa(integer, integer). count(N, Res, I, S). clauses summa(N, Res):- count(N, Res, 1, 0).ю count(N, Res, I, S):- I <= N,!, NewS = S + I, NewI = I + 1, count(N, Res, NewI, NewS). count(N, Res, I, S):- I > N, Res = S, write(“S=”), write(S).
Пример 3.4 predicates like(symbol, symbol). clauses like(tom, july). like(bill, mary). goal like(bill, X). Первый параметр запроса является входным, т.к. имеет значение, равное “bill”, второй параметр – X – свободная переменная, значение которой необходимо уточнить. В процессе поиска Пролог выдаст сообщение X = mary, при этом переменная X становится связанной и выступает как входной параметр для последующих целей. goal like(bill, X). like(Y, X). like(X, Z). В Прологе список входных и выходных аргументов для заданного предиката называется потоком параметров. Для предиката с двумя аргументами возможны 4 варианта потоков параметров: like(i, i). like(i, o). like(o, i). like(o, o).
i – input o – output
Правила могут возвращать свободную переменную и результаты вычислений. Запрос типа like(X, Y), имеющий поток параметров (о, о), передает в алгоритм поиска две последовательные задачи унификации. Если в базе фактов есть информация, соответствующая запросу, и указан предикат fail, требующий поиска всех возможных альтернатив для переменных X и Y, то Пролог выдаст множество вариантов: X = tom, Y = july. X = bill, Y = mary. При этом после определения значения переменной X Пролог меняет поток параметров: like(tom, Y), т.е. (i, o). На 3-ем шаге происходит откат назад: (о, о). При компиляции программ Пролог выполняет глобальный анализ потока параметров, начиная с основного целевого утверждения, затем проводится оценка всей программы. При этом поток параметров определяется для каждого обращения к каждому предикату. goal cursor(R, C), R1 = R+1, cursor(R1, C). Это – составная цель с последовательным выводом трех подцелей. При обращении к 1-му предикату поток параметров будет иметь вид (о, о), т.к. переменные R и С – свободные. 2-ая подцель вызывает связанную переменную R, значение которой должно быть определено ранее при вызове 1-го предиката. Переменная R1 является свободной. Если же в 1-ом предикате значение переменной R не было найдено, и она осталась свободной переменной, то Пролог выдал бы ошибку и остановил поиск. После вычисления R1 3-ий предикат вызывается с потоком параметров (i, i). Для каждого потока параметров, с которым вызывается пользовательский предикат, анализатор потока в Прологе проходит через составные предложения предиката, начиная с головы, и определяет, являются ли переменные – аргументы предиката – входными или выходными для анализируемого потока параметров. Примечание 1: Предикат not, вызываемый как самостоятельный предикат или как составной элемент правил, не работает, если он вызывается с выходным потоком параметров. Примечание 2: В предикатах, вызываемых с выходным потоком параметров, в структуре их высказываний должны определяться входные переменные, например, через ввод пользователем с клавиатуры значения переменной или вызова предиката инициализации, присваивающего переменной значения по умолчанию: init(X):- X = Æ., или в процессе унификации как сопоставление цели некоторым фактам в разделе init(X):- write(X). goal X = 5, init(X).
Тема 4. Факты. Факты характеризуют известные отношения между объектами, заданные в виде предикатов. При этом все объекты и отношения пишутся с маленькой буквы. Например: Джону нравится Мэри. like(john, mary). Следует соблюдать принятый порядок перечисления аргументов предикатов. Например: 1) Джон и Мэри играют в бадминтон. play(john, mary, badminton). 2) Джон дает книгу Мэри. gives(john, book, mary). Данные предикаты имеют различные порядки аргументов. Набор фактов в Прологе – это база фактов (БФ).
Запросы. Запросы – это целевые утверждения в форме предикатов, которые требуется подтвердить или опровергнуть в результате поиска по БФ. Например: 1)? – like(john, mary). Yes 2)? – like(john, ann). No Во втором случае ответ No, т.к. Пролог не нашел соответствующего факта в БФ, хотя в действительности ничего не известно о том, нравится ли Джону Анна. Примечание: Ответ No означает, что Пролог не может доказать истинность цели, однако ответ No не тождественен значению False для логической переменной или высказывания.
Переменные. Переменные используются в правилах и запросах с целью не конкретизировать объекты целевого утверждения, а заставить Пролог искать подходящие варианты. Каждый объект, начинающийся с большой буквы, воспринимается как переменная, причем длина имени переменной может быть большой. Например: 1) Что нравится Джону? 2) Есть ли что-либо, что нравится Джону? like(john, X) X = Is there Пролог различает два типа переменных: ü свободные (free); ü связанные (instantiated). Если переменная используется в предикате впервые, то ее значение не определено, и она считается свободной. Пролог ищет в БФ факт, соответствующий запросу и проводит унификацию, т.е. сопоставление свободной переменной какого-либо объекта, определенного из факта. Если такой факт найден, то переменная становится связанной, в том числе для всех последующих предикатов, в которых она встречается. В процессе унификации Пролог просматривает БФ сверху вниз в порядке следования фактов и маркирует первый найденный факт, соответствующий запросу. Если требуется найти не один, а множество фактов, соответствующих цели, то используют предикат fail, который заставляет Пролог продолжить поиск, начиная с факта, отмеченного маркером, и далее до конца БФ. Если Пролог находит другой факт, соответствующий запросу, то он стирает предыдущий маркер и маркирует новый найденный факт.
Правила. Правила – это обобщенные описания множества объектов и их отношений. Правила используются для указания зависимостей (типа 1:М, М:М) между фактами, где множество допустимых аргументов задается свободными переменными. При этом правила можно представить в виде дерева поиска. like(john, X):- female(X), like(X, wine),!, …. Это правило может быть представлено следующей структурой:
Составные цели в правилах образуются объединением нескольких предикатов подцели с помощью логических операторов and, or, not. Пролог последовательно старается подтвердить или опровергнуть составные подцели в порядке их указания. При этом каждая подцель маркируется своим маркером в процессе унификации. Пролог просматривает всю БФ для каждой подцели. Если 1-ая подцель подтверждена (маркер установлен), а 2-ая подцель – нет, то Пролог пытается переопределить 1-ую подцель. Процесс поиска, в котором Пролог последовательно подтверждает или опровергает составные цели, называется обратным отслеживанием. Пример 4.1 Backtracking % facts m1.1 ® like(mary, food). %f1 m1.2 ® like(mary, wine). %f2 m2.1 ® like(john, wine). %f3 like(john, mary). %f3 ? - like(mary, X), like(john, X). Алгоритм поиска: Шаг 1: ? - like(mary, X). X = food Пролог устанавливает маркер m1.1. Шаг 2: ? - like(john, food). false Шаг 3: Откат назад: X®free ? - like(mary, X). Поиск начинается от маркера m1.1. X = wine Предыдущий маркер стирается и устанавливается новый – m1.2. Шаг 4: ? - like(john, wine). Yes Устанавливается новый маркер – m2.1. Шаг 5 X = wine Примечание: Если нужно найти другие варианты ответов, то должен использоваться предикат fail, который выполняет откат назад и повторный поиск, начиная с маркеров m1.2 и m2.1 до тех пор, пока не будет просмотрена вся БФ для каждого из составных предикатов.
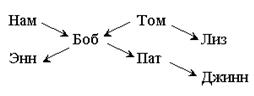
Рассмотренный пример программы использовал программирование с помощью фактов. Пример 4.2 Рассмотрим пример программирования с помощью правил. Пусть стоит задача поиска родственных отношений между людьми:
Запишем базу фактов, где будем использовать 3 типа предикатов: Predicates родитель(symbol, symbol) потомок(symbol, symbol) мужчина(symbol) женщина(symbol) % facts женщина (Нам). мужчина (Том). мужчина (Боб). женщина (Лиз). мужчина(Пат). женщина (Энн). мужчина (Джинн). родитель(нам, боб); родитель(том, боб); родитель(том, лиз); родитель(боб, энн); родитель(боб, пат); родитель(пат, джинн);
? – родитель(X, энн), родитель(X, пат). X=боб. потомок(X, Y):– родитель(Y, X). Исходя из дополнительной информации о поле родственников, можно определить новые отношения – “мать” и “сестра”: Правило, задающее материнство: мать(X,Y):– женщина(X), родитель(X, Y). Правило, определяющее термин «сестра»: сестра (X,Y):– родитель(Z, X), родитель (Z, Y),женщина(X). ? – сестра(X, пат). X=энн. Добавим предикат «предок» и зададим его рекурсивное определение. Будем говорить, что некто X и Z являются предком и потомком друг для друга, если между ними существует цепочка людей, связанных между собой отношениями «родитель». предок (X, Y):– родитель(X, Y). предок (X, Z):– родитель(X, Y), предок(Y, Z). ? – предок(нам, энн) Yes.
Тема 5. Основные понятия логического программирования. Предикат – это отношение между объектами. Атом – это имя конкретного объекта. Логическая переменная обозначает неопределенные объекты. С помощью логических переменных можно определить в программах структуру логических данных, называемых термами. При этом терм может быть константой, переменной, либо составной структурой. Структура содержит функтор – последовательность из одного или более элементов, являющихся термами. Функтор задается именем и числом аргументов: f(t1, …,tn); t/n. Примеры структур: S(0). not(milk). name(john, dough). foot(X). list (a, list, (b, nd)). tree(tree nd, 3, nit, 3, R). вопросы, цели и термы, не содержащие переменных, называются основными. Термы, содержащие переменные, называются не основными. Подстановкой называется некоторое множество пар вида: xi = tj, причем xi не входит в tj, xi ¹ tj, " i и j, xi ¹ xj, i ¹ j. Пример подстановки, состоящий из одной пары: X = milk. Подстановка может применяться к термам. Результат применения подстановки Q к некоторому терму А обозначается QA и представляет собой терм, полученный заменой каждого вхождения некоторой переменной x терма A на значение терма t для каждой пары (" x = t в Q).
Терм А называется примером В, если существует такая подстановка Q, что A = QB. Например, цель: like(john, wine). like(john, X).
sister(pat, list). sister(X, Y). В логических термах переменные-вопросы связаны квантором существования. Универсальные факты содержат переменные-утверждения (Все любят цветы): like(X, flowers). mult(0, X, 0). Из универсальных фактов можно вывести любой пример факта. Правило вывода называется конкретизацией. Общим примером термов А и В называется терм С, если он является примером А и примером В одновременно, т.е. существуют такое подстановки E = AQ1 = BQ2. Например, 2 терма: add (0, Y, 3) Q1 = 3. add (0, X, X) Q2 = 3. Общим при поиске ответов на вопрос с использованием факта лежит общий пример вопроса и факта. Если такой пример существует, то он является ответом на вопрос. Составные вопросы являются конъюнкцией. ? – Q1, Q2, …, Qn. Если каждая цель в вопросе независима, то ответ на вопрос – «да», если каждая цель выводится из программы, т.е. является следствием состояния, представленным вопросом, в котором существует одна или более общих переменных для разных целей: ? – p(x), q(x). Эту запись интерпретируется следующим образом: Существует ли такое x, что истинны цели p(x), q(x) одновременно? Переменные в составных вопросах связаны квантором существования. Общая переменная в этом случае используется для сокращения пространственного поиска значений переменных. Правилом называется утверждение вида АВ1, …, Bn при n > 0. Факт является частным случаем правила при n < 0. При n = 1 получаем рекурсию. В правилах переменные связаны квантором общности А, при этом область действия распространяется на все правила: сын(X, Y) отец(Y, X), мужчина(X). дочь(X, Y) отец(Y, X), женщина(X). дед(X, Z) отец(Y, X), отец(Y, Z). Возможны 2 варианта интерпретации правил: 1) Процедурный. Для ответа на вопрос: «Является ли некто X дедом Z?», - необходимо последовательно доказать истинность утверждения, что X является отцом Y, а Y является отцом Z. 2) Декларативный. С этой точки зрения правило истолковывается как логическая аксиома " X, Y, Z. Если X – отец Y и Y – отец Z, то X – отец Y и Y – отец Z, тогда X – дед Z. Для рассмотрения процедуры логического вывода используется закон, который в логике называется modus pones. Из некоторого правила R = (AB1, …, Bn) и фактов B’1, …, B’n выводится следствие А, если оно является примером правила R. Логическая программа Р – конечное множество правил. Некоторая цель G с кванторами является логическим следствием программы Р, если в программе найдется такое предпочтение с основным примером: A B1, …, Bn, и Bi, 1 < i < n, что высказывания Bi являются следствием программы, а следствие А является примером цели G. Примечание: Цель в логике – программа существует, когда она может быть выведена с помощью конечного числа применений правила modus pones. Процедура поиска ответа на вопрос отражает определенные логические следствия. Здесь угадывается основной пример цели и правила, затем рекурсивно ищется ответ на составной вопрос, соответствующий телу правила. Доказательство некоторой цели А в программе Р сводится к поиску правила: AiBi, …, Bn и указанию такой подстановки Q, что цель определяется как A = AiQ, а ВiQ – являются основными целями. Затем рекурсивно доказывается каждая составная цель в порядке указания логической программы, которая может включать альтернативные определения одних и тех же термов, что формально эквивалентно дизъюнкции. Например: родитель(X, Y) отец(X, Y). родитель(X, X) мать(X, Y). родитель(X, Y) отец(X, Y) or мать(X, Y). Указанная совокупность правил с одинаковым именем предиката называется процедурой.
Пример 5.2 сын(X, Y):- родитель(Y, X), M(X). % R ? – сын(петя, вася) 1-ая редукция снимает цель и строит 2 производные цели на основе наиболее общего примера R, найденного в программе. 2-ая и 3-я редукции подтверждают поставленные подцели и не создают новых производных целей. Дерево вывода выглядит следующим образом:
родитель(вася, петя) М(вася) Значением логической программы Р называется множество основных единичных целей М(Р), выводимых из программы. Примечание: Значением программы, содержащим только факты, является сама программа. Программа Р корректна относительно некоторого заданного значения Mi, если оно является подмножеством всех значений данной программы Mi Î M(P). Другими словами, программа корректна, если вычисляет только то, что требуется. Программа Р называется полной, если она вычисляет все возможные значения программы. Цель называется истинной относительно подразумеваемого значения, если цель входит в данное значение (выводится из него). В противном случае цель называется ложной. Унификация является основой автоматической дедукции и логического вывода в задачах искусственного интеллекта. Унификатором 2-х термов А и В называется такая подстановка Q, которая делает их равными: AQ = BQ. Если существует унификатор 2-х термов, то такие термы называются унифицируемыми. Каждый унификатор характеризует общий пример терма. Для каждого терма возможно множество общих примеров. Для 2-х унифицируемых термов существует единственный наиболее общий унификатор. Алгоритм унификации находит наиболее общий унификатор 2-х термов, если таковой существует. Общая схема алгоритма унификации: T1Q = T2Q. Q -? Будем считать, что Q – ячейка памяти. 1) Q = 0. Стек: T1, T2, отказ = false. 2) Пока стек не пуст и не отказ Do считать X = Y из стека ветвление: 1. X-переменная, не входящая в терм Y: замена всех Х в стеке и в языке программирования Q на Y. 2. Y-переменная, X-терм: замена Y на X. 3. X = Y: ® продолжить 4. X-функтор X = f(q1, …, qn) и Y-функтор Y = f(q1, …, qn), т.е. X и Y – составные термы: поместить Xi и Yi " 3) Если термы не унифицируемы, то отказ = true иначе результат хранится в Q. Этот алгоритм использует стек для хранения входных равенств, подлежащих решению, и язык программирования Q для хранения результата подстановки. В цикле из стека считается и обрабатывается на каждом шаге одно равенство. Пример 5.3 1) like(john, wine) = like(john, X). X = wine 2) a(b, C, d(e, F)) = a(B, c, d(E, f)). Если переменные, обозначенные большими буквами, являются свободными, то они принимают значения переменных, обозначенных маленькими буквами: B = b, С = с,E = e, F = f.
Тема 6. Экспертные системы (ЭС). Типы задач, решаемых ЭС.
Примечание: Возможно совмещение различных задач в реальных ЭС.
Типовая структура ЭС.
1) Приобретение знаний – это сбор, передача и анализ опыта решения проблем из необходимых источников знаний в БЗ ЭС. В качестве источников знаний выступают: ü люди-эксперты; ü
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.142.113 (0.015 с.) |

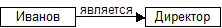

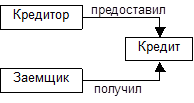 Для такой сети конкурентные утверждения о предметной области соответствуют присвоению значений узлам сети. Т.е. «Альфа-банк» может быть и кредитором, и заемщиком, в зависимости от ситуации.
Для такой сети конкурентные утверждения о предметной области соответствуют присвоению значений узлам сети. Т.е. «Альфа-банк» может быть и кредитором, и заемщиком, в зависимости от ситуации.


 сын(петя, вася)
сын(петя, вася) в стек.
в стек.



