
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предоставление данных в 2 формате.Содержание книги Поиск на нашем сайте
Система счислений 1.1.Система счисления - это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: Различают два типа систем счисления:
Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является десятичная система, используемая повседневно. Любое целое число в позиционной системе можно записать в форме многочлена: Формула Гарде
Где А –значение разряда X- основание системы n – номер позиции Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F). Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами.
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления, числа записываются с помощью двух символов (0 и 1).
Предоставление данных в 2 формате. Система кодирования данных двоичным кодом основана на предоставлении данных последовательностью двух знаков – 0 и 1. Эти знаки называют двоичными цифрами - битами. Одним битом могут быть выражены два понятия: 0 или 1 (да или нет, чёрное или белое, истина или ложь и т.п.). Если количество битов увеличить до двух, то уже можно выразить четыре различных понятия. Тремя битами можно закодировать восемь различных значений. Кодирование целых и действительных чисел: Арифметические операции. В двоичной системе счисления арифметические операции выполняются по тем же правилам, что и в десятичной системе счисления, т.к. они обе являются позиционными (наряду с восьмеричной, шестнадцатеричной и др.). Сложение Сложение одноразрядных двоичных чисел выполняется по следующим правилам: 0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10 В последнем случае, при сложении двух единиц, происходит переполнение младшего разряда, и единица переносится в старший разряд. Переполнение возникает в случае, если сумма равна основанию системы счисления (в данном случае это число 2) или больше его (для двоичной системы счисления это не актуально). Сложим для примера два любых двоичных числа: + 101 ------ Вычитание Вычитание одноразрядных двоичных чисел выполняется по следующим правилам: 0 - 0 = 0 1 - 0 = 1 0 - 1 = (заем из старшего разряда) 1 1 - 1 = 0 Пример: - 101 ---- Умножение Умножение одноразрядных двоичных чисел выполняется по следующим правилам: 0 * 0 = 0 1 * 0 = 0 0 * 1 = 0 1 * 1 = 1 Пример: * 10 ------ + 0000 ------ Деление Деление выполняется так же как в десятичной системе счисления: 1110 | 10 |---- 10 | 111 ---- ---- ----
And (логическое сложение)
Or(логическое умножение)
XOR(исключающее или)
a b a XOR b 0 0 0 0 1 1 1 0 1 1 1 0 NOT(отрицание) a NOT a 0 1 1 0 Параллельная передача.
Последовательная передача.
При параллельной передаче данных для каждого передаваемого бита используется один провод.(соответственно одновременно по нескольким проводам передаются одновременно несколько битов).при такой передаче улучшается помехозащищенность на расстояние до 0.5 метра, частота не более 133 мГц. При последовательной передаче за один такт такт проходит один бит и идут они друг за другом по одному проводу.(частота 250 мгц)
Дешифратор Преобразует входной код в выходной по определенному правилу Линейный дешифратор – преобразует из 2-ой в 10-ую,взодной бинарный код, соответствующий десятичному значению Счетный триггер
Вход1: любой положительный импульс меняет состояние триггера (первый – единицу,второй сбрасывает ноль) 4-ех разрядный счетный триггер: установка триггера по заднему фронту импульса. Свойства: 1)любой импульс на Т вход перекидывает переход из одного состояния в другое. 2)используется как для счетчиков-делителей так и для временных состояний импульсов.
2.ЭВМ Процессор Классификация CISC, RISC. CISC- предназначен для решения любых задач. Недостатки: · Высокая стоимость аппаратной части · Сложности с распараллеливанием вычислений RISC- предназначен для решения строго определенных задач. Недостатки: · Нефиксированное значение длины команд · Арифметическое действие кодируется одной командой · Небольшое количество регистров, каждый из которых выполняет определенную задачу. Режимы работы процессора 1)Реального времени: однопрограммный
Первоначально персональные компьютеры фирмы IBM могли адресовать только 1 Мбайт оперативной памяти. Это решение, принятое в начале развития персональных компьютеров, продолжало соблюдаться и в последующее время — в каждом компьютере следующего поколения процессор должен был уметь работать в режиме совместимости с процессором Intel 8086. Этот режим назвали реальным. Когда процессор работает в реальном режиме, он может обращаться к памяти только в пределах 1 Мбайт (как и процессор Intel 8086), и не может использовать 32-разрядные и 64-разрядные операции. Процессор попадает в реальный режим сразу же после запуска. В реальном режиме работают операционные системы DOS и стандартные DOS-приложения.
2)Защищенный многозадачный - мультипрограммный режим все задачи квотируются по времени и по регистрам. Или подрежимы: 1)Квота времени 2)Вытеснение
3)Виртуальный –запускается под защищенным режимом, создается несколько виртуальных 86 процессоров для решения задач. Структура команды POH. Структура команды INTEL.
Код Оператор Оператор Оператор Операции 1 2 3
Адрес данных, Адрес 2 с которыми будут работать Ассемблеры INTEL двухадресовые. Длина команды – 1-6 байт. Результат операции помещается в первый операнд. Виды адресации: -прямая -память(косвенная) сегмент:смещение,указывается только смещение, для адреса данных используются сегментные регистры – DS,SS,ES смещение может указываться как базовое, индексное и базово-индексное.
DS [Bx+Si] Сюда запоминаем
Память.
Ввод/ Вывод Адрес контроллера Прерывание Прерывание -приостановка выполнения текущей программы и вызов программы обрабатывающей данные прерывания по завершению программы управления передаётся приостановленной программе INT XX-команда при которой процессор реализов.прерывания прерывание
программные аппаратные системные маскируемые программные немаскируемые Немаскируемые- такие прерывание невыполненные, которых приводит к отказу системы (DRAM,регистр памяти, конденсатор) Стек- память для временного хранения состояние процессора в точку возврата (Lifo и Fifo в IBM-Lifo) Маскируемые- те которые можно замаскировать (запретить) используются для организации ввода\вывода. Система счислений 1.1.Система счисления - это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: Различают два типа систем счисления:
Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является десятичная система, используемая повседневно. Любое целое число в позиционной системе можно записать в форме многочлена: Формула Гарде
Где А –значение разряда X- основание системы n – номер позиции Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F). Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами.
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления, числа записываются с помощью двух символов (0 и 1).
Предоставление данных в 2 формате. Система кодирования данных двоичным кодом основана на предоставлении данных последовательностью двух знаков – 0 и 1. Эти знаки называют двоичными цифрами - битами. Одним битом могут быть выражены два понятия: 0 или 1 (да или нет, чёрное или белое, истина или ложь и т.п.). Если количество битов увеличить до двух, то уже можно выразить четыре различных понятия. Тремя битами можно закодировать восемь различных значений. Кодирование целых и действительных чисел: Арифметические операции. В двоичной системе счисления арифметические операции выполняются по тем же правилам, что и в десятичной системе счисления, т.к. они обе являются позиционными (наряду с восьмеричной, шестнадцатеричной и др.). Сложение Сложение одноразрядных двоичных чисел выполняется по следующим правилам: 0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10 В последнем случае, при сложении двух единиц, происходит переполнение младшего разряда, и единица переносится в старший разряд. Переполнение возникает в случае, если сумма равна основанию системы счисления (в данном случае это число 2) или больше его (для двоичной системы счисления это не актуально). Сложим для примера два любых двоичных числа: + 101 ------ Вычитание Вычитание одноразрядных двоичных чисел выполняется по следующим правилам: 0 - 0 = 0 1 - 0 = 1 0 - 1 = (заем из старшего разряда) 1 1 - 1 = 0 Пример: - 101 ---- Умножение Умножение одноразрядных двоичных чисел выполняется по следующим правилам: 0 * 0 = 0 1 * 0 = 0 0 * 1 = 0 1 * 1 = 1 Пример: * 10 ------ + 0000 ------ Деление Деление выполняется так же как в десятичной системе счисления: 1110 | 10 |---- 10 | 111 ---- ---- ----
And (логическое сложение)
Or(логическое умножение)
XOR(исключающее или)
a b a XOR b 0 0 0 0 1 1 1 0 1 1 1 0 NOT(отрицание) a NOT a 0 1 1 0
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.69 (0.006 с.) |

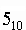 ;
;  ;
;  и т. д.
и т. д.








