
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Очереди. Очереди с приоритетом.Содержание книги Поиск на нашем сайте СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 4 1 ЗАДАЧИ НА ГРАФАХ.. 5 2 ОЧЕРЕДИ. ОЧЕРЕДИ С ПРИОРИТЕТОМ.. 6 2.1 Основные подходы к реализации очередей. 7 2.2 Основные подходы к реализации очередей с приоритетом. 9 2.2.1 Бинарная куча.................................................................................. 10 2.2.2 Биномиальная куча. 12 2.2.3 Куча Фибоначчи. 14 3 СТРУКТУРА ДАННЫХ 2-3 КУЧА.. 16 3.1 Вставка в кучу. 19 3.2 Извлечение приоритетного элемента из кучи. Поиск. Слияние. 23 3.3 Изменение ключа произвольного элемента кучи. 25 3.4 Обход по куче. 27 4 СРАВНИТЕЛЬНЫЙ АНАЛИЗ ОЧЕРЕДЕЙ С ПРИОРИТЕТОМ.. 28 5 ОПТИМИЗАЦИЯ АЛГОРИТМОВ НА ГРАФАХ.. 31 5.1 Алгоритм Дейкстры.. 31 5.2 Алгоритм Прима. 34 ПОДВЕДЕНИЕ ИТОГОВ...36 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ...37 ПРИЛОЖЕНИЕ А: ИНТЕРФЕЙС РЕАЛИЗАЦИЙ ОЧЕРЕДЕЙ С ПРИОРИТЕТОМ ПРИЛОЖЕНИЕ Б: ЛИСТИНГИ ОСНОВНЫХ ОПЕРАЦИЙ 2-3 КУЧИ
ВВЕДЕНИЕ В компьютерных науках и программировании в целом очень важны быстродействие алгоритмов и их надежность, а если излагаться конкретнее, то необходимы оптимизации, которые ведут к ускорению работы алгоритма, уменьшению требования к ресурсам и при этом сохраняя уровень надежности на должном уровне. Вопрос оптимизации алгоритмов очень многогранен, поэтому целью моей работы будет оптимизация алгоритмов на графах, а точнее оптимизация определенного класса задач на графах. Оптимизация, изложенная в этой работе будет существенно ускорять выбор из множества (например, выбор ближайшего города в алгоритме Дейкстры для поиска кратчайшего пути). В этой работе будут кратко описаны некоторые родственные понятия, но описаны они будут на минимальном уровне, чтобы обеспечивать связь между понятиями. Далее будут рассмотрены основные подходы к реализации очередей с приоритетом, описание 2-3 кучи, сравнительный анализ.
ЗАДАЧИ НА ГРАФАХ Графы повсеместно используются в информатике для задач, связанных с взаимным расположением объектов, или сводимым к ним задач. Приведем пример задач, которые решаются на графах: · Поиск кратчайшего пути между парой вершин · Поиск Гамильтонова цикла минимального веса в графе. · Поиск минимального ациклического подграфа, которые включает в себя все вершины (поиск минимального остового дерева). Мною не случайно были выбраны именно эти алгоритмы. Дело в том, что решение каждой из этих задач подразумевает выбор из множества некоторого самого оптимального решения для следующей итерации. Например, для первой задачи можно использовать алгоритм Дейкстры и тогда нам будет необходимо на каждой итерации выбирать вершину, которая не была выбрана и ближе всего к начальной. Для второй задачи (задача Коммивояжера) необходимо определять кратчайший путь между текущей вершиной, и множеством ещё не пройденных вершин при решении задачи алгоритмом выбора ближайшего соседа. Для последней задачи можно использовать алгоритм Прима, где также необходимо получать минимальные пути от любой вершины из множества выбранных, до ближайшей из множества не выбранных. Эти задачи (в которых необходимо выбирать оптимальное значение из множества) мы отнесем в отдельный класс. Данная работа направлена на оптимизацию именно этого класса задач на графах. В каждом случае при решении в лоб мы должны на каждой итерации дополнительно тратить n итераций для определения минимума. Было бы не плохо иметь структуру данных, которая позволила бы получать значение минимума быстрее чем за линейное время (в идеале за константное). И в этом нам помогут очереди, а точнее очереди с приоритетом. Бинарная куча Бинарные кучи также называют частично упорядоченными деревьями, поскольку порядок задается только между родителями и детьми, в тоже время как порядок между братьями или другими вершинами может быть выбран произвольно. Пример кучи, построенной на бинарном дереве предоставлен на рисунке 2.4
Рисунок 2.4 – Бинарная куча
Бинарную кучу обычно представляют и реализуют в виде массива. Такой выбор обусловлен тем, что куча сбалансирована, поэтому представление её как массива является тривиальной задачей. Хранение данных в виде массива, очевидно, экономнее, нежели в виде древовидной структуры. Применяется следующее правило для представления кучи в виде массива: если родительская вершина имеет индекс i, то её сыновья имеют индексы 2*i + 1 и 2*i + 2 соответственно (при индексации с нуля). Тогда куча на рисунке выше будет выглядеть следующим образом 100 19 36 17 3 25 1 2 7 Для вставки в бинарную кучу применяют следующий механизм: Помещаем вершину в конец массива, потом сравниваем с родителем. Если родитель менее приоритетный, меняемся с ним местами. Производим данную процедуру до тех пор, пока не восстановим свойства кучи. Этот механизм называется просеивание вверх. В качестве примера вставим в кучу вершину 43 100 19 36 17 3 25 1 2 7 43 = 100 19 36 17 43 25 1 2 7 3 = 100 43 36 17 19 25 1 2 7 3 Для изменения ключа модифицируем его значение на нужное, после чего при помощи просеивания восстанавливаем свойства кучи. Например, поменяем значение ключа 100 на 14 14 43 36 17 19 25 1 2 7 3 = 43 14 36 17 19 25 1 2 7 3 = 43 25 36 17 19 14 1 2 7 3 Для удаления ключа заменим первый элемент последним, после чего восстановим свойства кучи. Пример: 43 25 36 17 19 14 1 2 7 3 = 3 25 36 17 19 14 1 2 7 = 36 25 3 17 19 14 1 2 7 = 36 25 14 17 19 3 1 2 7 Одной из основных проблем бинарной кучи является отсутствие эффективного алгоритма для слияния куч. В бинарных кучах в качестве слияния можно использовать последовательное добавление всех элементов из кучи b в кучу a. Следующая куча, которая будет рассмотрена, имеет эффективный алгоритм объединения.
Биномиальная куча Биномиальная куча - это множество биномиальных деревьев, каждое из которых удовлетворяет свойству кучи (рисунок 2.6). Биномиальное дерево — это дерево, определяемое по индукции: B0 – дерево, состоящее из одного узла. Bi – дерево, состоящее из двух биномиальных деревьев Bi-1 Если рассмотреть дерево степени n, то на i уровне будет
Рисунок 2.5: Пример биномиальных деревьев
Рисунок 2.6: Пример биномиальной кучи Для поиска приоритетного элемента достаточно пройти по всем корневым вершинам, и выбрать приоритетное. (Также можно хранить указатель на приоритетную вершины) Для слияние куч мы сперва объединяем два дерева в одно, при этом вершины должны следовать в порядке возрастания степеней. Деревья одинаковых степеней мы сливаем между собой. Процесс соответствует двоичному сложению, то есть сложение двух деревьев степени n даст дерево степени n+1. Пример сложения степеней: 1-2-3-5 + 2-3-4 = 1-2-2-3-3-4-5 = 1-3-3-3-4-5 = 1-3-4-4-5 = 1-3-5-5 = 1-3-6 Данная операция корректна, так как согласно структуре Бинома Ньютона дерево степени n имеет 2n вершин, а 2n + 2n = 2n+1 Таким образом добавление элемента в кучу можно определить, как слияние текущей кучи с кучей из одного элемента (куча степени 0) Для удаления из кучи приоритетного элемента необходимо сперва найти такой элемент, затем удалить из дерева корневой элемент. В результате дерево степени n распадется на деревья степеней 0,1.. n-1. Доказать этот факт можно при помощи тождества 2n – 1 = 2n-1 + 2n-1 – 1 2n-1 – 1 = 2n-2 + 2n-2 – 1. … 21 – 1 = 20 + 20 – 1 = 20 Значит 2n -1 = Для уменьшения ключа присваиваем ему новое значение, после чего при помощи просеивания поднимаем его вверх до тех пор, пока не восстановим свойства кучи. Биномиальная куча дает логарифмическое время для всех основных операций. Однако не смотря на это данная куча не очень популярна. Это вызвано тем, что существуют кучи, которые работают быстрее при тех же затратах памяти (Бинарная куча, например, используется благодаря экономному расходу памяти, простоты реализации, и представления). Следующая куча, которая будет рассмотрена, является модернизированной версии биномиальной кучи, и ускоряет скорость работы некоторых операция до константных.
Куча Фибоначчи Фибоначчиева куча — набор деревьев Фибоначчи, корни которых объединены в неупорядоченный циклический двусвязный список. В отличие от биномиальной кучи, степени корней не обязаны быть попарно различными (Рисунок 2.8) Дерево Фибоначчи - биномиальное дерево, где у каждой вершины удалено не более одного ребенка (Рисунок 2.7)
Рисунок 2.7: Дерево Фибоначчи высоты 4
Рисунок 2.8: Куча Фибоначчи
Вставка в кучу подразумевает добавление в список дерева степени 0 (дерево из одной вершины). Таким образом куча вырождается в список (Рисунок 2.9).
Рисунок 2.9: Вырожденная куча из 10 элементов
Объединение двух куч заключается в связывании крайних элементов двух куч. (Рисунок 2.10) Рисунок 2.10: Добавления к исходной куче кучи 12-13-11 Для удаления из кучи вершины изменим ее значение ключа на -
Рисунок 2.11: Куча после удаления элемента с ключом 11
Данная операция выполняется за логарифмическое время, но из-за того, что куча может быть частично или полностью вырождена в список появляется скрытая константа, из-за которой эффективность операции снижается. Операция уменьшения значения ключа заключается в вырезании элемента из кучи, и вставке его в корневой список. В случае если новое значение ключа менее приоритетно чем у родителя, вырезание не производиться. Преимущества кучи Фибоначчи над биномиальной в том, что операции, не требующие удаления, работают за константное время, а те что требуют удаления – за логарифмическое. Кучи Фибоначчи обладают лучшей асимптотикой по сравнению с биномиальной и бинарной, но и в них есть один недостаток. Операция удаления зависит от сбалансированности кучи, и если мы часто добавляем элементы в кучу, и редко извлекаем, то её быстродействие ухудшается. Были рассмотрены основные подходы к реализации очередей с приоритетом. Вопросом оптимизации куч Фибоначчи, направленных на уменьшение скрытой константы занялся Tadao Takaoka, который в своей работе Theory of 2-3 Heaps описал структуру данных, которая способна решить данную проблему.
СТРУКТУРА ДАННЫХ 2-3 КУЧА Основная проблема куч Фибоначчи заключалась в том, что балансировка кучи происходит только при удалении из кучи. Если бы мы смогли реализовать структуру данных, которая будет сохранять балансировку и при добавлении в кучу(слиянии), но при этом сохранив асимптотику, то удалось бы получить выигрыш в производительности. И эта структура – 2-3 куча. 2-3 куча — это массив 2-3 деревьев, определенных по индукции: B0 дерево состоит из одного или двух элементов Bi дерево, состоит из Bi* + Bi-1 Bi* дерево, состоящее из Bi-1 + Bi-1 (Рисунок 3.1).
Рисунок 3.1: дерево 2-3 кучи
2-3 дерево - это сбалансированное дерево, родительский узел которого может иметь как два, так и три сына (Рисунок 3.2). 2-3 деревья относятся к деревьям и являются идеально сбалансированными. Высота дерева из n вершин лежит в диапазоне [ На рисунках 7.1 и 7.2 приведен пример 2-3 дерева, и 2-3 дерева кучи:
Рисунок 3.2: 2-3 дерево Раз мы ограничились в слиянии только деревьев одной степени, необходимо их классифицировать, и для этого введем два понятия: Степень дерева– высота корневого узла Насыщенность дерева– Наличие у корневого элемента партнерской связи (подробнее при описании структуры узла). По насыщенности будем различать: насыщенные(t) и ненасыщенные(f) деревья. Тогда в куче будем xранить деревья по следующему принципу: в i ячейке дерева можно хранить только дерево степени i. Как говорилось ранее дерево степени 0 содержит в себе или 1, или 2 вершины. Тогда в случае если дерево хранит 1 вершину, это ненасыщенное дерево степени 0(0f), а если 2 вершины, то это насыщенное дерево степени 0(0t). Насыщенное дерево при добавлении к нему вершин переходит в ненасыщенное более высокой степени. Дерево степени 1 будет хранить 3 или 6 вершин соответственно. Тогда насыщенное дерево степени n будет хранить в себе 3n вершин, а ненасыщенное 3n+3n = 2*3n вершин. Таким образом насыщенное дерево является объединением двух ненасыщенных деревьев. Тогда максимальное количество элементов в куче из n деревьев выражается как
Таблица 2: Пример деревьев 2-3 кучи Теперь самое время затронуть детали реализации и описать структуру узла 2-3 кучи (Рисунок 3.3):
Рисунок 3.3: Структура узла 2-3 кучи на примере 1f дерева Где: K (key) – ключ, определяет приоритет элемента V (value) – значение, которое храниться вместе с ключом pr (parent) – родительский узел, элемент с более высоким приоритетом сh(child) – дочерний узел, элемент с более низким приоритетом pt (partner) – партнерский узел. При объединении двух f деревьев они соединяются как партнеры. При этом узлы, подчиненные одному из партнеров непосредственно с другим партнером связей не имеют. Также имеет место нюанс: необходимо как-то помечать того партнера, который является более приоритетным. Во-первых, это позволит избежать лишних проверок при выполнении всех основных операций, во-вторых поможет избежать проблем при обходе кучи, в-третьих если партнер будет являться сыном, мы сразу будем знать по какому из них нужно возвращаться к родителю, и при этом ссылку на родителя у менее приоритетного элемента хранить не обязательно. Будем помечать самого приоритетного из двух соседей флагом sl(sister in law).Также для корневого элемента эта метка будет определять факт насыщенности дерева. ln(left neighbor) – левый сосед rn(right neighbor) – правый сосед Необходимость соседской связи, и особенность реализации будет обозначена при описании алгоритма вставки.
Вставка в кучу
Теперь рассмотрим основные операции над кучей, и начнем с операции вставки. Операция вставки определяется как слияние исходной кучи с кучей из одного дерева (если вставляем один элемент, то дерева 0f). В куче не может существовать два дерева одинаковой степени, поэтому пря появлении таковых мы будем их объединять до тех пор, пока все степени не будут различны. Может возникнуть две ситуации при слиянии куч: В самом простом случае при добавлении в кучу дерева может оказаться, что ячейка массива свободна, тогда просто занимаем её. В противном случае, если ячейка уже занята, будем производить слияние. (Рисунок 3.4)
Рисунок 3.4: Схема вставки в кучу
Слияние через партнера возникает, когда оба дерева ненасыщенные. В таком случае, раз оба дерева не имеют партнера, для объединения их достаточно просто связать их как партнеров. Операцию можно выразить формулой: nf + nf = nt (Рисунок 3.5)
Рисунок 3.5: Вставка через партнера
Слияние через сына выглядит несколько сложнее. В самом примитивном варианте, когда деревья степени 0, это выглядит так: из двух корневых элементов выбирается самый приоритетный (в случае если он из насыщенного дерева, мы его меняем местами с корневым элементом из ненасыщенного дерева), к нему добавляет насыщенное дерево как сына. При этом, раз степень дерева увеличилась, его необходимо вставлять заново (так как n+1 ячейка может быть занята). Общая формула: nf + nt = (n+1)f
Рисунок 3.6: Вставка через сына
Но тут возникает одна проблема, а что если деревья не нулевой степени (у каждого из деревьев уже есть сын)? В этом случае нам и пригодиться соседская связь. Мы отделяем сына от самого приоритетного элемента, и добавляем его как соседа к самому приоритетному из насыщенного дерева (помеченное как sl). Данная манипуляция представлена на рисунке 3.7 (на примерах 1f + 1t = 2f и 2f+2t = 3f): Рисунок 3.7: Пример использования соседской связи
К слову о соседских связях: использование левого соседа было описано выше, зачем же тогда правый сосед? Правый сосед используется как обратная связь, зацикливая переходы через соседей. Например, для 3f дерева из примера выше самая верхняя соседская связь будет выглядеть так: 10 Существует ещё одна разновидность слияния – делением. Деление применяется в том случае, когда необходимо объединить две насыщенные вершины. При операции вставки не существует такой ситуации, при которой эта операция необходима, однако, данная операция имеет место при удалении. Опишем алгоритм вставки в кучу делением. Из двух корневых вершин выберем самую приоритетную, и отделим от соседней. Отделенную вершину будем объединять через сына с насыщенным деревом. Таким образом если мы имели два дерева nt, на выходе будем иметь nf + (n+1) f. После этих манипуляций nf дерево оставляем лежать в ячейке, а (n+1) f вставляем заново.
Рисунок 3.8: Вставка Делением
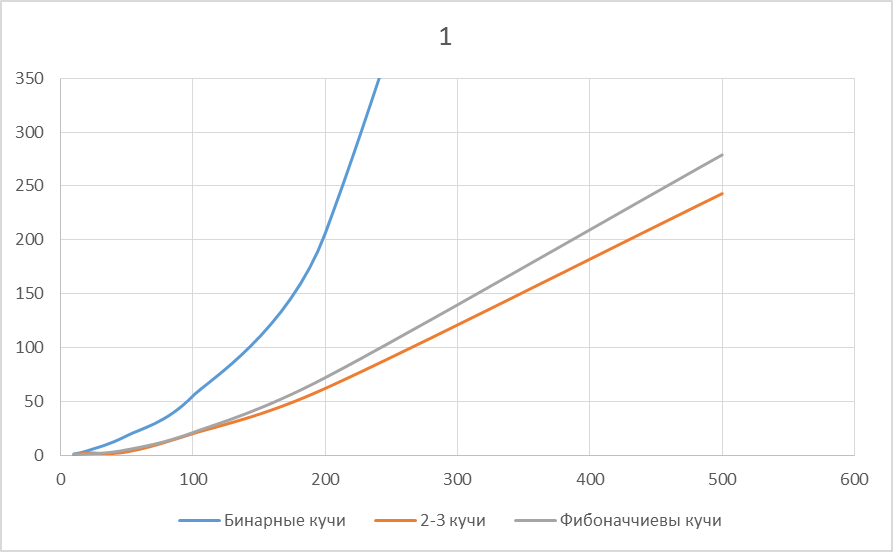
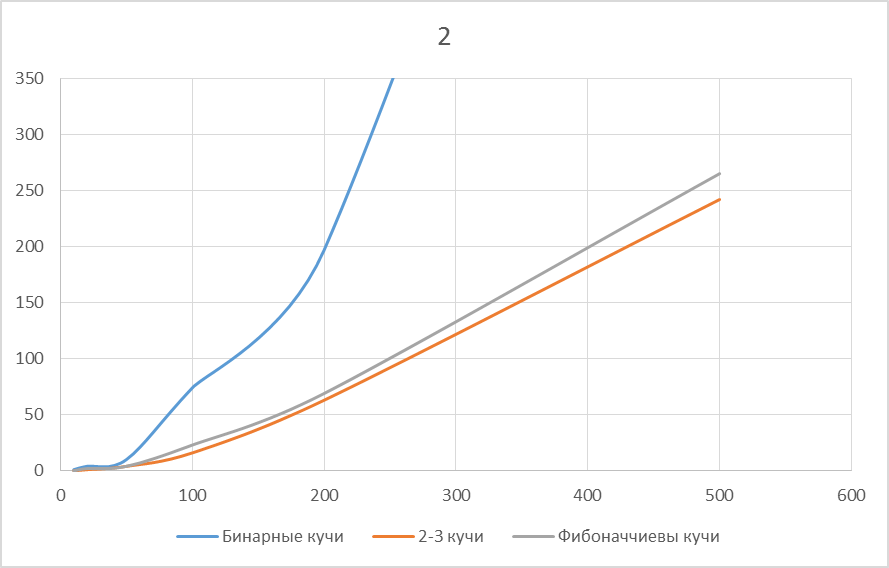
Теперь, когда все операции рассмотрены, самое время поговорить о реализации. Вставка будет разделена на два блока: интерфейс вставки и слияние. Интерфейс вставки будет отвечать за выборку двух сливаемых деревьев (вставляемое дерево + дерево, занимающее позицию), и обработку результата модуля слияния. В случае, когда позиция свободна модуль будет размещать дерево в нужной ячейке, в обратном же случае он будет отдавать управление модулю слияния. Модуль слияния отвечает за выбор алгоритма слияния, и приведение его в исполнение. На выход будут отдаваться ссылки на вставленное дерево (если нету, то NULL), и дерево, которое необходимо вставить (если нету, то NULL). Второй случай возникает тогда, когда в результате слияния степень дерева изменилась. Вставка через партнера возвращает вставленное дерево. Вставка через сына возвращает дерево, которое необходимо вставить. Вставка слиянием возвращает два дерева. Вставка не зависит от количества элементов в куче, а зависит от количества деревьев. Но поскольку количество деревьев в куче в данный момент времени не зависит от количества элементов, то операция вставки не зависит от размера кучи, следовательно, операция работает за O(1). Обход по куче Мы разобрали основные алгоритмы, однако я приведу ещё один алгоритм: обход по куче. Этот алгоритм необходим для утилизации кучи и для выполнения некоторых функций, например, получение указателей на все вершины. Обход по куче будем выполнять по аналогии с обходом деревьев рекурсивной процедурой: Обойти сына Обойти партнера Обойти соседа Выполнить функцию На сына идем при условии, что он присутствует. На партнера при условии, что он непомеченный (так как мы начинаем обход из корневой вершины, то в первую очередь приходим на помеченного соседа, поэтому рекурсию будем запускать только для непомеченного). С обходом соседа все несколько сложнее. Так как соседи образуют циклическое кольцо, необходимо сначала выделить это кольцо, а затем выполнить обход из каждой вершины кольца. Затем выполнить функцию и для самих элементов кольца. В завершении шага рекурсии выполняем функцию для текущей вершины при условии, что она не равна вершине захода. Вершина захода устанавливается, когда мы обходим циклическое кольцо соседей для того, чтобы к корню не применялась функция до того, пока не обойдутся все элементы поддерева. Если этого не делать, то при вызове деструктора (деструктор в нашем случае вызывает обход, удаляя каждый элемент) корень дерева удалиться раньше, чем элементы, что приведет к утечке памяти. Рисунок 3.12: Пример обхода дерева кучи (вершины помечены в порядке обхода) Алгоритм Дейкстры Начнем с алгоритма Дейкстры. Суть оптимизации будет заключаться в следующем: Будем поддерживать кучу, в которой будут храниться минимальные пути от стартовой вершины, до каждой. Тогда вместо поиска минимального расстояния в массиве мы будем извлекать это значение из кучи за гораздо меньшее время. Когда в ходе алгоритма будут находиться более короткие пути, будем добавлять их в кучу. Алгоритм будет выполняться до тех пор, пока куча не станет пустой. Проведем сравнительный анализ зависимости количества вершин от времени работы для разных плотностей графов. От 1 до 4 будем уменьшать плотность графа:
Рисунок 5.1: Плотность графа = 1
Рисунок 5.2: Плотность графа = 0.5
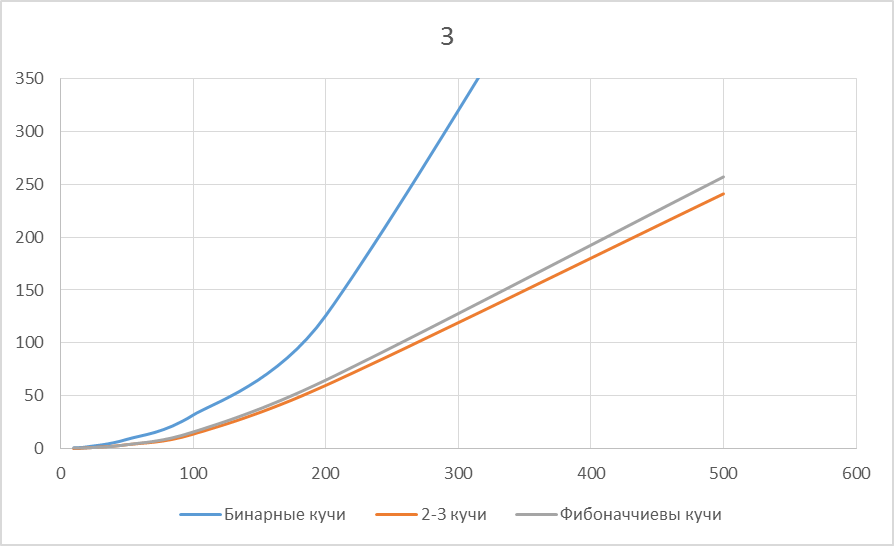
Рисунок 5.3: Плотность графа = 0.2
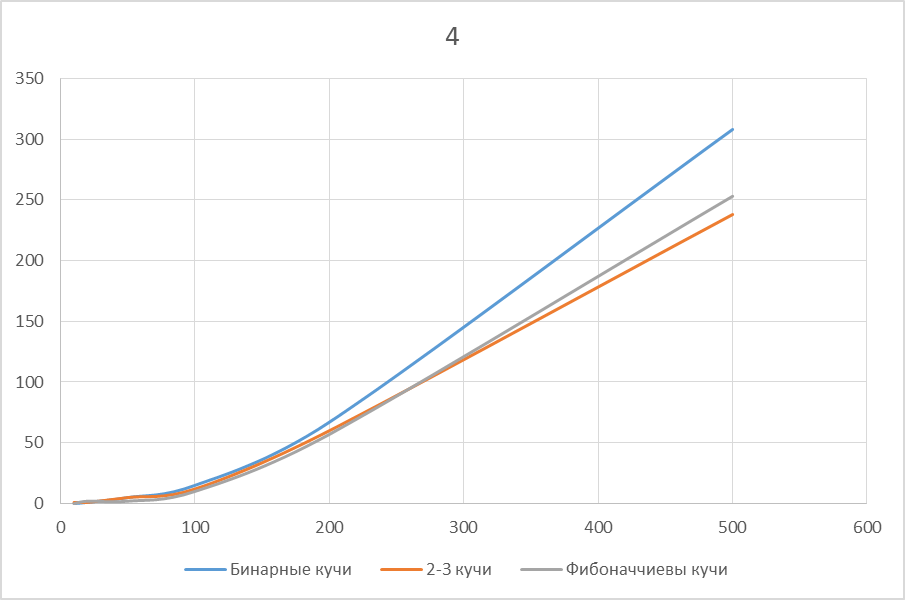
Рисунок 5.4: Плотность графа = 0.05
При уменьшении плотности графа графики стремятся к одинаково оптимальным решениям. Однако на плотных графах только 2-3 кучи дают заметный прирост по отношению к Бинарным кучам и до 20% по отношению к Фибоначчиевым кучам. На разреженных графах все три структуры данных работают практически одинаково, однако 2-3 куча все равно дает немного лучший результат. Таким образом 2-3 куча является самой оптимально работающей в плане быстродействия при любых случаях по отношению к Бинарной и Фибоначчиевой куче.
Алгоритм Прима Алгоритм Прима подразумевает выбор ближайшей вершины из множества доступных и не посещенных, поэтому и здесь имеет место оптимизация при помощи очереди с приоритетом. Механизм схожий с примененным в алгоритме Дейкстры: Сначала в очередь загружаем стартовую вершину, затем выгружаем все смежные с ней вершины в очередь, и так до тех пор, пока очередь не станет пустой или не пометим все вершины. При тестировании не учитывался факт наличия остова, так как граф генерировался случайным образом. Если в графе нет остова, алгоритм отработает медленнее, так как условием выхода будет полное опустошение очереди, а в случае с наличием остова выход из алгоритма, как правило, возникает раньше. Также в тестировании используется реализация на массиве. На графиках 8-10 приведены результаты тестирования для плотного графа, графа с плотностью 0.5, и разреженного графа.
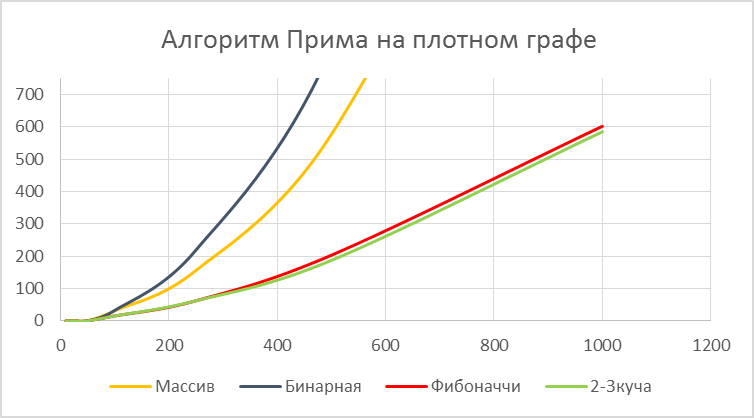
Рисунок 5.5: Алгоритм Прима на плотном графе.
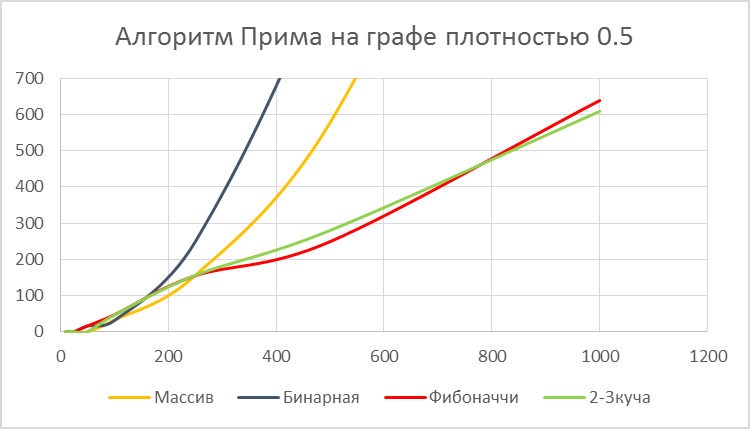
Рисунок 5.6: Алгоритм Прима на графе плотностью 0.5.
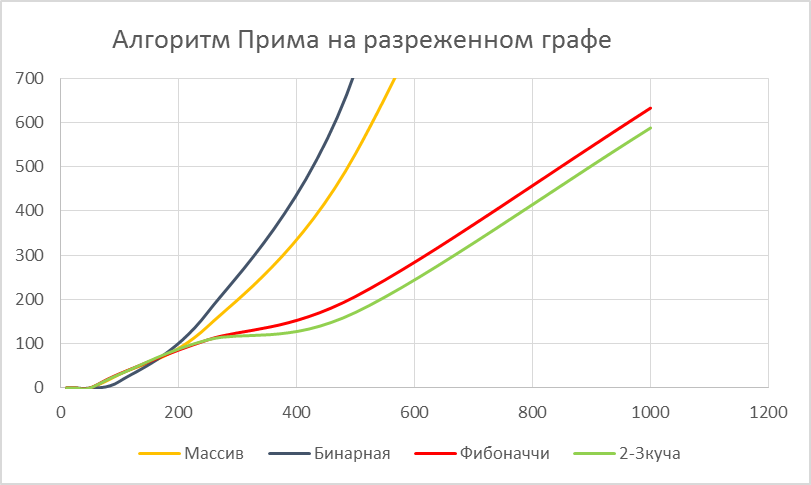
Рисунок 5.7: Алгоритм Прима на разреженном графе.
Из графиков видно что Бинарная куча, взятая из std::priority_queue не годится в целях оптимизации по скорости. Фибоначчиев куча и 2-3 куча жестко конкурируют, однако с ростом количества вершин 2-3 куча начинает превосходить кучу Фибоначчи. ПОДВЕДЕНИЕ ИТОГОВ Тестирование показало, что в среднем при оптимизации алгоритмов на графах прирост быстродействия при выборе 2-3 кучи достигает 20%. Мною также был рассмотрен алгоритм выбора ближайшего соседа для решения задачи коммивояжера, и сортировка кучей. В обоих случаях была отмечена приблизительно та же зависимости, что и при описанных в данной работе алгоритмах. Все вышесказанное продемонстрировало стабильную и оптимальную работу 2-3 кучи по отношению к Бинарным и Фибоначчиевым кучам. Если Бинарные кучи все ещё занимают место лидера по критерию экономии памяти, то Фибоначчиевы кучи уступают 2-3 кучам по всем критериям. Класс алгоритмов на графах, в которых используется выбор приоритетного из множества замечательно оптимизируется при помощи 2-3 куч. На данный момент времени 2-3 кучи менее популярны чем другие структуры данных, и это скорее всего обусловлено тем, что 2-3 кучи были описаны сравнительно недавно, и их реализация более трудоемкая. В сети интернет и литературных источниках информация почти отсутствует, поэтому я использовал первоисточник, из которого черпал идею, и проводил аналогию с другими кучами. На выходе получилась структура данных, которая способна улучшить быстродействие не только отдельных алгоритмов, но и разного рода систем массового обслуживания, и вообще всего, что связано с обработкой данных в порядке приоритета. По данным тестирования можно вывести правило выбора очереди с приоритетом: Бинарную кучу следует выбирать тогда, когда накладываются ограничения на требуемые ресурсы, либо, когда необходимо в условиях жесткого ограничения по времени реализовать рабочую очередь с приоритетом. Кучу Фибоначчи следует выбирать тогда, когда предъявляются требования на быстродействие алгоритмов обработки информации, при этом реализацию нужно проводить в сжатые сроки. Также следует что должно быть известно, что вероятность операции удаления приблизительно равна операции вставки, либо если это не так, это существенным образом не отразится на работе системы в целом. 2-3 Кучу следует выбирать при тех же требованиях, что и кучу Фибоначчи, но если запас времени на реализацию больше, либо есть запас высококвалифицированных разработчиков, способных реализовать эту структуру данных в сжатые сроки. Биномиальную кучу не следует использовать кроме специфических частных случаев.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 4 1 ЗАДАЧИ НА ГРАФАХ.. 5 2 ОЧЕРЕДИ. ОЧЕРЕДИ С ПРИОРИТЕТОМ.. 6 2.1 Основные подходы к реализации очередей. 7 2.2 Основные подходы к реализации очередей с приоритетом. 9 2.2.1 Бинарная куча.................................................................................. 10 2.2.2 Биномиальная куча. 12 2.2.3 Куча Фибоначчи. 14 3 СТРУКТУРА ДАННЫХ 2-3 КУЧА.. 16 3.1 Вставка в кучу. 19 3.2 Извлечение приоритетного элемента из кучи. Поиск. Слияние. 23 3.3 Изменение ключа произвольного элемента кучи. 25 3.4 Обход по куче. 27 4 СРАВНИТЕЛЬНЫЙ АНАЛИЗ ОЧЕРЕДЕЙ С ПРИОРИТЕТОМ.. 28 5 ОПТИМИЗАЦИЯ АЛГОРИТМОВ НА ГРАФАХ.. 31 5.1 Алгоритм Дейкстры.. 31 5.2 Алгоритм Прима. 34 ПОДВЕДЕНИЕ ИТОГОВ...36 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ...37 ПРИЛОЖЕНИЕ А: ИНТЕРФЕЙС РЕАЛИЗАЦИЙ ОЧЕРЕДЕЙ С ПРИОРИТЕТОМ ПРИЛОЖЕНИЕ Б: ЛИСТИНГИ ОСНОВНЫХ ОПЕРАЦИЙ 2-3 КУЧИ
ВВЕДЕНИЕ В компьютерных науках и программировании в целом очень важны быстродействие алгоритмов и их надежность, а если излагаться конкретнее, то необходимы оптимизации, которые ведут к ускорению работы алгоритма, уменьшению требования к ресурсам и при этом сохраняя уровень надежности на должном уровне. Вопрос оптимизации алгоритмов очень многогранен, поэтому целью моей работы будет оптимизация алгоритмов на графах, а точнее оптимизация определенного класса задач на графах. Оптимизация, изложенная в этой работе будет существенно ускорять выбор из множества (например, выбор ближайшего города в алгоритме Дейкстры для поиска кратчайшего пути). В этой работе будут кратко описаны некоторые родственные понятия, но описаны они будут на минимальном уровне, чтобы обеспечивать связь между понятиями. Далее будут рассмотрены основные подходы к реализации очередей с приоритетом, описание 2-3 кучи, сравнительный анализ.
ЗАДАЧИ НА ГРАФАХ Графы повсеместно используются в информатике для задач, связанных с взаимным расположением объектов, или сводимым к ним задач. Приведем пример задач, которые решаются на графах: · Поиск кратчайшего пути между парой вершин · Поиск Гамильтонова цикла минимального веса в графе. · Поиск минимального ациклического подграфа, которые включает в себя все вершины (поиск минимального остового дерева). Мною не случайно были выбраны именно эти алгоритмы. Дело в том, что решение каждой из этих задач подразумевает выбор из множества некоторого самого оптимального решения для следующей итерации. Например, для первой задачи можно использовать алгоритм Дейкстры и тогда нам будет необходимо на каждой итерации выбирать вершину, которая не была выбрана и ближе всего к начальной. Для второй задачи (задача Коммивояжера) необходимо определять кратчайший путь между текущей вершиной, и множеством ещё не пройденных вершин при решении задачи алгоритмом выбора ближайшего соседа. Для последней задачи можно использовать алгоритм Прима, где также необходимо получать минимальные пути от любой вершины из множества выбранных, до ближайшей из множества не выбранных. Эти задачи (в которых необходимо выбирать оптимальное значение из множества) мы отнесем в отдельный класс. Данная работа направлена на оптимизацию именно этого класса задач на графах. В каждом случае при решении в лоб мы должны на каждой итерации дополнительно тратить n итераций для определения минимума. Было бы не плохо иметь структуру данных, которая позволила бы получать значение минимума быстрее чем за линейное время (в идеале за константное). И в этом нам помогут очереди, а точнее очереди с приоритетом. ОЧЕРЕДИ. ОЧЕРЕДИ С ПРИОРИТЕТОМ. Повседневно мы часто сталкиваемся с понятием очереди. Покупки в магазине, пробки, ожидание ответа от интернет ресурса – все это так или иначе связано с очередями. Очередь – абстрактный тип данных с правилам доступа к элементам по принципу «первый пришёл — первый вышел» (FIFO, first-in-first-out). В соответствии с этим принципом у очереди есть начало (точка, откуда происходит удаление) и конец (точка, куда добавляются вершины). Однако не всегда порядок выхода зависит от порядка входа. В этом случае говорят об очередях с приоритетом. Очередь с приоритетом — абстрактный тип данных, поддерживающий две обязательные операции — добавить элемент и извлечь приоритетный. Предполагается, что для каждого элемента можно вычислить его приоритет — действительное число или в общем случае элемент линейно упорядоченного множества. Очередь с приоритетом для множества элементов из A и заданной функцией Приоритет элемента — это некоторая числовая характеристика, описывающая важность элемента множества относительно других. В общем случае приоритет может задаваться как отображение x где x – идентификатор элемента (значение) y – Приоритет элемента (ключ). Порядок следования элементов можно задавать при помощи логической функции f (x, y) которая вернет ИСТИНА если x приоритетнее y, и ЛОЖЬ в противном случае (функция приоритетности). Таким образом очередь может быть реализована внутри очереди с приоритетом. Примером очереди с приоритетом может быть очередь на игровой сервер с vip системой, очередь в поликлинику по талонам (Человек может прийти последним, но по талону на данное время, и тогда он пройдет первым) и т.д.
|
||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 526; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |


 вершин. Обычно биномиальные деревья представляются в виде корневого списка в порядке возрастания степеней (Рисунок 2.5)
вершин. Обычно биномиальные деревья представляются в виде корневого списка в порядке возрастания степеней (Рисунок 2.5)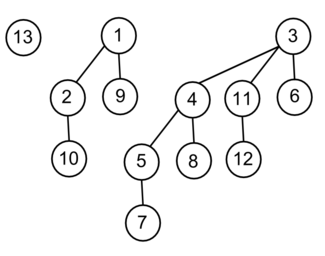






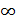 , и затем, чтобы восстановить свойства кучи просеем её к корневому списку. Если у удаляемой вершины есть дети, помещаем их к корневому списку. Далее начинается балансировка кучи, которая выполняется только при удалении, и нужна для того, чтобы куча не был вырождена в список. Суть балансировки заключается в следующем: берем две вершины степени n и объединяем их в дерево степени n+1, при этом в корне будет самый приоритетный из элементов, а менее приоритетный станет сыном. (Рисунок 2.11)
, и затем, чтобы восстановить свойства кучи просеем её к корневому списку. Если у удаляемой вершины есть дети, помещаем их к корневому списку. Далее начинается балансировка кучи, которая выполняется только при удалении, и нужна для того, чтобы куча не был вырождена в список. Суть балансировки заключается в следующем: берем две вершины степени n и объединяем их в дерево степени n+1, при этом в корне будет самый приоритетный из элементов, а менее приоритетный станет сыном. (Рисунок 2.11)

 ] Однако 2-3 деревья из-за своей структуры занимают много памяти, так как фактическая информация храниться только в листьях, а узлы используются для адресации на нужный лист. В целях экономии произведем модификацию: Будем хранить данные по тому же принципу, что и в бинарных деревьях. Мы сможем себе это позволить в том случае если условимся объединять только деревья одной степени, что нам в принципе и надо.
] Однако 2-3 деревья из-за своей структуры занимают много памяти, так как фактическая информация храниться только в листьях, а узлы используются для адресации на нужный лист. В целях экономии произведем модификацию: Будем хранить данные по тому же принципу, что и в бинарных деревьях. Мы сможем себе это позволить в том случае если условимся объединять только деревья одной степени, что нам в принципе и надо.
 . Примеры некоторых деревьев:
. Примеры некоторых деревьев:




 8
8 
 представляет собой абстрактный тип данных, в котором элементы расположены согласно приоритету элементов.
представляет собой абстрактный тип данных, в котором элементы расположены согласно приоритету элементов. y,
y,


