
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы теории чисел. Функция ЭйлераСодержание книги Поиск на нашем сайте
Историей теории чисел занимались Евклид, Ферма, Эйлер В истории основоположником явл.Эйлер. Число называется простым, если оно делится на единицу и на самого себя,если имеются др.делители,то число назыв. составное. В случае маленького числа легко определить простое оно или составное. Для больших чисел требуются доп.средства. Поиск больших простых чисел важнейшая задача в криптографии, в частности с шифрованием с откр.ключом. Кроме умножения двух чисел, сущ. и обратная задача-задача факторизации, т.. нахождения 2-ухи более чисел,дающих при умножении искомое число. Функция Эйлера. Формулу Эйлера удобно исп.для больших х, если разложение числа n на простые множители; для криптографии формула Эйлера важна тем, что она позволяет легко получить число для простых и некоторых др.чисел; Эйлер был одним из 1-ых,кто использовал алгоритм Евклида в арифметической форме. Функция Эйлера Например, для числа 24 существует 8 меньших него и взаимно простых с ним чисел (1, 5, 7, 11, 13, 17, 19, 23), поэтому
Основы теории чисел. НОД и НОК Алгоритм Евклида-это алг нахожд ниабольшего общего делителя (НОД)пары целых чисел Наибольший общий делитель(НОД)-это число,которое делит без остатка 2 числа и делится само без остатка на любой другой делитель данных 2-х ч-л Это большое ч-о,на которое можно без остатка разделить 2 ч-а,для котрых ищется НОД Описание алг нахожд НОД делением 1-большое ч-о делим на меньшее 2-если делится без остатка,то меньшее ч-о и есть НОД(выход из цикла) 3-если есть остаток,то большое число заменяем на остаток от деления Нахожд наименьшего общего кратного(НОК)данных чисел Наименьшим общим кратным данных натур-х ч-л,кратное каждому из данных ч-л Напр,НОК(24,42)=168-это самое маленьк ч-о которое делиттся и на 24,на 42 Нахожд наименьш-о общего кратного Для нах-ния НОК нескольких данных натур-х ч-л надо: 1-разложить каждое из данных ч-л на простые множители 20выписать разложение большего из ч-л и умнож его на недостающие множители из разложения др ч-л Наименьшее кратное 2-х взаимно простых ч-л =произведению этих ч-л Особый случай нахожд НОК: 1-если одно из исходных ч-л делится нацело на др-е,то НОК этих ч-л=этому числу(нок(60,15)=60) 2-т к взаимно простые ч-а не имеют общих простых делителей,то их НОК= произведению этих ч-л(нок(8,9)=72) Теория сравнений A=в(mod m) если двум целым a и в отвечает один и тот же остаток m, то они наз равно статочными по модулю m или сравнимыми по модулю m 1) Если а-в в делится на m то а=в(mod m) Пр. 15=1(mod 7) т.к 15-1=14, а 14 кратное 7. 2) Если а=в (mod m) c=d(mod m),то а+с=в+d, ас=вd(mod m) Пр 13=5(mod 8) 11=3(mod 8), то 13+11=5+3=0(mod m), 13*11=5*3=7(mod8) 3) Если а=в(mod m), то 4) Если ас=вс (mod m), то взаимно простое сm Пр 1200=45(mod 7) Тогда 1200=15*80и45=15*3, то 80=3(mod 7)
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.159.148 (0.008 с.) |

 - мультипликативная арифметическая функция, равная количеству натуральных чисел, меньших n и взаимно простых с ним. При этом полагают по определению, что число 1 взаимно просто со всеми натуральными числами, и
- мультипликативная арифметическая функция, равная количеству натуральных чисел, меньших n и взаимно простых с ним. При этом полагают по определению, что число 1 взаимно просто со всеми натуральными числами, и 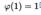 .
.
 =
=  (mod m), К N между этими буквами знак полуавал.
(mod m), К N между этими буквами знак полуавал.


