
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плотностью тела называется отношение массы тела к его объемуСодержание книги
Поиск на нашем сайте
В системе СИ плотность измеряется в кг/, а в системе СГС в г/. Удельным весом называется отношение веса тела к его объему
В системе СИ удельный вес измеряется в H/м3, а в системе СГС в дин / см3. Согласно второму закону Ньютона вес P=mg, где g – ускорение силы тяжести. Тогда удельный вес можно представить в виде произведения плотности тела на ускорения силы тяжести: δ =
При изменении температуры тела изменяется и его плотность, так как изменяется его объем. Зависимость плотности тела от температуры выражается формулой:
где Существует несколько способов определения плотности твердых тел. Если тело имеет правильную геометрическую форму, то его плотность легко определить, измерив его объем и массу. Если тело имеет неправильную геометрическую форму, то его объем определяют с помощью мензурки или применяют метод гидростатического взвешивания. Для определения объема мелких и сыпучих твердых тел, а также для определения плотности жидкости применяют специальный прибор – пикнометр. В настоящей лабораторной работе определяется плотность твердых тел правильной геометрической формы, объем которых легко рассчитать по соответствующим формулам. К телам правильной геометрической формы в частности относятся: шар, для которого объем:
где R – радиус, D – диаметр шара. Цилиндр, для которого объем:
Полый цилиндр, для которого объем;
где D – внешний диаметр цилиндра, Н – его высота, d – внутренний диаметр цилиндра. Параллелепипед, для которого объем V = a*b*c, где а – высота, b – длина, с – ширина параллелепипеда.
II. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Определите массу тела на технических весах, соблюдая при этом правила работы с ними. Обратите внимание на точность взвешивания на технических весах. 2. Измерьте линейные размеры тела штангенциркулем. Измерения произведите три раза и вычислите средние значения. 3. По средним значениям линейных размеров вычислите объем тела. 4. Измерьте линейные размеры тела микрометром (по три раза каждый размер) и вычислите по средним данным объем тела. 5. Вычислите плотность тела по средним значениям массы и объема тела отдельно для измерений тела штангенциркулем и микрометром
6. Рассчитать абсолютные ошибки измерений массы и линейных размеров тела. 7. Вычислите относительные ошибки измерения плотности тела по формуле: Е где m – среднее значение массы тела, 8. Вычислите абсолютные ошибки измерений плотности по формуле (отдельно для микрометра и штангенциркуля):
9. Данные измерений и вычислений занесите в таблицы. 10. Запишите ответы в виде: 11. Оцените относительную ошибку измерений плотности в процентах и запишите в таблицу 2. 12. Сделайте выводы. Таблица 1 Определение объема тела
Таблица 1 дана для параллелепипеда. Для цилиндра вместо а, в, с будет D. и Н и т. д.
Таблица 2 Определение плотности тела
Формулы для подсчета относительных ошибок измерений объема тел правильной геометрической формы Для шара: где D – среднее значение диаметра, ΔD – средняя абсолютная ошибка измерений диаметра. Для цилиндра: где D и Н среднее значение диаметра и высоты соответственно, ΔD и ΔН – средние абсолютные ошибки измерений диаметра и высоты цилиндра. Для полого цилиндра: где D и d – средние значения внешнего и внутреннего диаметров соответственно, ΔD и Δd – средние значения абсолютных ошибок измерений внешнего и внутреннего диаметров соответственно, Н – среднее значение высоты цилиндра, ΔН – среднее значение абсолютных ошибок измерений высоты. Для параллелепипеда: где а, в, с – средние значения высоты, длины и ширины соответственно, Δа, Δв, Δс – средние значения абсолютных ошибок измерений.
Контрольные вопросы
1. Какие измерения называются прямыми и косвенными? Приведите примеры. 2. Какие ошибки называются систематическими и случайными? От чего они зависят? 3. Какие ошибки измерений называются абсолютными и относительными? Какова размерность этих ошибок? 4. Дайте понятие веса и массы тела, плотности и удельного веса. Каковы единицы измерения этих величин? 5. Сформулируйте законы Ньютона и закон всемирного тяготения. 6. Расскажите устройство штангенциркуля и микрометра. 7. Как зависит плотность от температуры?
ЛАБОРАТОРНАЯ РАБОТА №2 ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЕ МАТЕМАТИЧЕСКОГО МАЯТНИКА И ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ.
ЦЕЛЬ РАБОТЫ: изучить законы колебательного движения, определить ускорения силы тяжести. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: математический маятник, секундомер, набор шариков, линейка.
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Движение, при котором тело или система тел через равные промежутки времени отклоняется от положения равновесия и вновь возвращается к нему, называются периодическими колебаниями. Колебания, при которых изменение колеблющейся величины со временем происходит по закону синуса или косинуса, называются гармоническими. Уравнение гармонического колебания записывается в виде:
Гармонические колебания характеризуются следующими параметрами: амплитудой А, периодом Т, частотой υ, фазой φ, круговой частотой ω. А – амплитуда колебания – это наибольшее смещение от положения равновесия. Амплитуда измеряется в единицах длины (м, см и т. д.). Т – период колебания – это время, в течении которого совершается одно полное колебание. Период измеряется в секундах. υ – Частота колебания – это число колебаний, совершаемых в единицу времени. Измеряется в Герцах. φ – фаза колебания. Фаза определяет положение колеблющейся точки в данный момент времени. В системе СИ фаза измеряется в радианах. ω – круговая частота измеряется рад/с Всякое колебательное движение совершается под действием переменной силы. В случае гармонического колебания эта сила пропорциональна смещения и направлена против смещения:
где К – коэффициент пропорциональности, зависящий от массы тела и круговой частоты.
Примером гармонического колебания может служить колебательной движение математического маятника. Математическим маятником называют материальную точку, подвешенную на невесомой и недеформируемой нити. Небольшой тяжелый шарик, подвешенный на тонкой нити (нерастяжимой), является хорошей моделью математического маятника.
Рис.1 Пусть математический маятник длиной l (рис. 1) отклонен от положения равновесия ОВ на малый угол φ ≤
При малых углах φ можно записать:
где Х – дуговое смещение маятника от положения равновесия. Тогда получим:
Знак минус указывает на то, что сила F направлена против смещения Х. Итак, при малых углах отклонения математический маятник совершает гармонические колебания. Период колебаний математического маятника определяется формулой Гюйгенса:
где Из последней формулы видно, что период колебания математического маятника зависит лишь от длины маятника и ускорения силы тяжести и не зависит от амплитуды колебания и от массы маятника. Зная период колебания математического маятника и его длину, можно определить ускорение силы тяжести по формуле:
Ускорением силы тяжести называется то ускорение, которое приобретает тело под действием силы притяжения его к земле. На основании второго закона Ньютона и закона всемирного тяготения можно записать:
где М – масса Земли, равна R – расстояние до центра Земли, равное Т. к. Земля не имеет форму правильного шара, то на различных широтах имеет разное значение, а, следовательно, и ускорение силы тяжести на разных широтах будет разное: на экваторе
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 = m / v.
= m / v. δ = P/V.
δ = P/V.
 ;
; - плотность тела при 0оС,
- плотность тела при 0оС,  - коэффициент объемного расширения тела, t – температура тела.
- коэффициент объемного расширения тела, t – температура тела.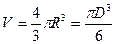
 ; где D – диаметр цилиндра, Н – его высота.
; где D – диаметр цилиндра, Н – его высота.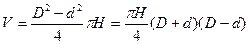 ,
,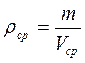

 - средняя абсолютная ошибка измерения массы тела,
- средняя абсолютная ошибка измерения массы тела,  - средняя относительная ошибка измерения объема (формулы для вычисления относительных ошибок измерений объема тела даны в примечаниях к данной работе).
- средняя относительная ошибка измерения объема (формулы для вычисления относительных ошибок измерений объема тела даны в примечаниях к данной работе).
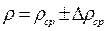 .отдельно для измерений плотности тела штангенциркулем и микрометром.
.отдельно для измерений плотности тела штангенциркулем и микрометром.
 %
%
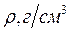


 ,
,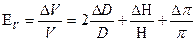 ,
, ,
,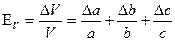
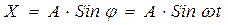
 ,
,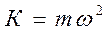
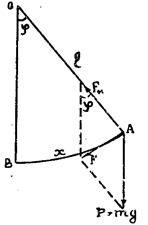
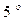 . На шарик действует сила тяжести
. На шарик действует сила тяжести  , направленная вертикально вниз, и сила упругости нити
, направленная вертикально вниз, и сила упругости нити  , направленная вдоль нити. Равнодействующая этих сил F будет направлена по касательной к дуге АВ и равна:
, направленная вдоль нити. Равнодействующая этих сил F будет направлена по касательной к дуге АВ и равна:



 - длина маятника, т. е. расстояние от точки подвеса до центра тяжести маятника.
- длина маятника, т. е. расстояние от точки подвеса до центра тяжести маятника.


 ,
,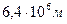 ,
, ; на полюсе
; на полюсе  ; на средней широте
; на средней широте  .
.


