Правильные и неправильные умозаключения в логике высказываний.
Классификация понятий.
Понятия классифицируются по объему:
Общее- если его объему принадлежит более одного элемента.
Единичное- если его объему принадлежит только один элемент.
Пустое- если его объему не принадлежит ни одного элемента.
Закон обратного отношения объема и содержания понятий.
П1, П2- понятия
с (П1) - содержание понятия
о (П1) - объемы понятий
задачи по теме- " понятия"
1ый тип: по заданным понятиям определить их объемы, установить отношения между этими объемами проиллюстрировать эти отношения с помощью диаграммы Эйлера.
2ой тип: по заданной д. Эйлера найти понятия отношения между объёмами которых иллюстрирует эта диаграмма.
примеры задач 1ого типа-" человек"- множество всех людей
" студент"- множество всех студентов
"англичанин"- множество всех англичан
"народ"-множество всех народов
18. Фрагмент естественного языка, изучаемый в силлогистике.
4 разновидности высказываний:
1) все S есть P
2)некоторые S есть P
3) все S не есть P
4) некоторые S не есть P
1,4 высказывания- общие, 3,4- некоторые
высказывания 1) и 2) вида называются утвердительными
высказывания 3) и 4) вида наз. отрицательными
высказывания 1ого типа- общеутвердительные
высказывания 2ого типа- частноотрицательные
высказывания 3его типа- общеотрицательные
высказывания 4ого типа- частноотрицательные
С точки зрения силлогистики выделяют 3 составляющие: субъект, предикат и логическая связка.
Субъект высказывания- это термин, который обозначает то, о чём говорится в данном высказывании.
Предикат- это термин, который означает, что говорится о субъекте. Обозначается буквой Р.
Логическая связка- это неполная лингвистическая конструкция, следующего вида:
Все… есть
Некоторые….есть
Все….не есть
Некоторые….не есть
19. Логический квадрат.
Логический квадрат- графическое изображение отношений между высказываниями в силлогистике, при условии, что у этих высказываний одни и те же субъекты и одни и те же предикаты.
2 высказывания находятся в отношении противоречия, если они не могут быть вместе истинными и не могут быть вместе ложными.
2 высказывания находятся в отношении противоречия, если они не могут быть вместе истинными, но могут быть вместе ложными.
2 высказывания находятся в отношении подпротивоположности, если они не могут быть вместе ложными, но могут быть вместе истинными.
20. Формальный язык силлогистики. Его синтаксис и семантика.
Формальная силлогистика, значит, использующая формальный язык.
Алфавит ФЯС:
(1) t1, t2,t3- термы.
(2) A E I O- логические связки ФЯС.
Формулой в ФЯС называется любая последовательность, содержащая 3 члена- 1ый из которых является логической связкой ФЯС, а 2ой и 3ий являются термами ФЯС.
Семантика в ФЯС.
1. интуитивная семантика в ФЯС.
2. теоретико-множественная семантика ФЯС.
термы обозначают термины, то есть существенные и описания, выражающие понятия. логическим связкам соответствуют неполные синтаксические конструкции. А- все...есть, Е-все... не есть, I- некоторые...есть, О- некоторые...не есть.
Теоретико-множественная семантика ФЯС.
Определение оценки ФЯС в непустом универсальном множестве U: оценкой ФЯС в непустом универсальном множестве U наз. любое приписывание терма ФЯС непустым подмножеством, множества U, при котором данному терму ФЯС приписывается 1 единственное подмножество.
Следования в силлогистике.
Формула А ФЯС следует в формальной силлогистике из множества М формул ФЯС, если для всякого непустого множества U и всякой оценке VU формального языка силлогистике в универсальном множестве U верно следующее: если значение при Vu всякой формулы из М есть истина, то и значение Vu формулы А есть истина.
22. Правильные и неправильные умозаключения в силлогистике.
Умозаключением в формальной силлогистике называется последовательность формул ФЯС, содержащая более 1 члена вместе с утверждением о том, что последняя из этих формул следует в формальной силлогистике из множества всех предшествующих в этой последовательности формул.
Умозаключение в формальной силлогистике называется правильным, если его заключение следует в формальной силлогистике из множества всех его посылок.
Умозаключение в формальной силлогистике называется неправильным, если его заключение не следует в формальной силлогистике из множества всех его посылок.
Умозаключения по аналогии.
Аналогия - это умозаключение о принадлежности предмету определенного признака на основе сходства в признаках с другим предметом.
Аналогия дает не строго достоверные, а правдоподобные выводы. Поэтому, чтобы не получить ложных результатов, ею нужно пользоваться осторожно.
В логике различают:
1) аналогию предметов, когда сравниваются признаки предметов. «дом – как большой муравейник», «вертолет – это большая стрекоза»;
2) структурную аналогию, когда сходными оказываются структурные признаки. Например: «печень по структуре напоминает губку»;
3) функциональную аналогию, когда аналогичным являются принципы действия, функционирования. Например, аналогия кровообращения и инфраструктуры общества;
4) каузальную (причинно-следственную) аналогию, когда у сравниваемых предметов существует одна и та же причина поступка. Например, аналогичные мотивы разных преступлений, общие предпосылки геофизических явлений.
Различают два вида аналогии: аналогию предметов и аналогию отношений.
Аналогия предметов. В данном умозаключении объектом уподобления выступают два единичных предмета, события или явления, а переносимым признаком являются свойства этих предметов.
Аналогия отношений - это умозаключение, в котором объектом уподобления выступают отношения между двумя парами предметов, а переносимым признаком являются свойства этих отношений.
Также выделяют аналогию строгую, нестрогую и ложную.
Строгая аналогия применяется в научных исследованиях, в математических доказательствах.
Нестрогая аналогия дает не достоверное, а вероятное заключение. Например, испытание прочности моста на модели, затем построение настоящего моста.
При нарушении правил применения аналогии аналогия может дать ложное заключение, т. е. стать ложной. Вероятность заключения по ложной аналогии равна нулю.
Для получения более вероятных выводов по аналогии требуется, возможно большее сходство между сравниваемыми предметами или явлениями.
29. Определения.
Определение(дефиниция) - это логическая процедура, состоящая в придании фиксированного смысла языковым выражением.
В языковой практике определения применяются для решения различных задач.
В философии например термин "понятие" употребляется на интуитивном уровне и имеет весьма туманное значение.
Также к примеру выражение- человек есть по дефиниции политическое животное- представляет собой констатацию того, что термин "человек" будет употребляться в смысле " политическое животное". Такого рода констанции выражают конвенции (соглашения об употреблении терминов).
Также существуют явные определения. Явными определениями называются определения, задаваемые лингвистической конструкцией вида. A t- В
Пример: А.С. Пушкин по определению автор Евгения Онегина- является дефиницией имени конкретного индивида.
Также существуют неявные определения- это определения, задаваемые лингвистической конструкцией вида: t есть по дефиниции то, что удовлетворяет условиям В1,В2...Вn.
30. Доказательства (прямые и косвенные (методом от противного)).
Теорема 1.
Если формулы ФЯЛВ
А1,…,Аn->В
таковы, что умозаключение
А1,…,Аn->В
является правильным в формальной логике высказываний, то формулы (А1&…&An Ↄ B) являются законом формальной логики высказываний.
Прямое. В пользу тезиса собираем аргументы, убеждаемся что они верны и выводим тезис.
А1,…, Аn ─>Тезис
Косвенное. Демонстрация того, что нападать на тезис бесполезно. Мы не ищем аргументы «за», вместо того, чтобы тезис защищать аргументами, нападаем.
Например, у нас есть тезис Т. Мы нападаем и говорим «не Т!», получается неприятность. А неприятность никому не нравится, тогда смотрим, откуда же взялась неприятность? Ах! Потому что мы допустили «не Т», в таком случае, отказываемся от «не Т», получается «не «не Т»», следовательно, Т. Таким образом мы показали что бесполезно нападать.
Теорема 2.
Если А1,…,Аn, В есть формулы в ФЯЛВ и А1&…&An Ↄ B есть закон ФЛВ, то умозаключение А1,…,Аn->В является правильным в ФЛВ.
Доказательство методом от противного.
(1) Неверно, что Т2 (допущение)
(2) А1,…Аn, В есть формула в ФЯЛВ и А1&…&An Ↄ B есть закон ФЛВ (из 1 по таблице)
(3) Умозаключение А1,…,Аn->В не является правильным в ФЛВ. (из 1 по таблице)
(4) В не следует в ФЛВ из посылок А1,…,Аn. (Из (3), по определению правильного умозаключения в ФЛВ).
(5) Существует такая оценка ФЯЛВ, при которой все посылки А1,…Аn принимают значение истины, а заключение принимает значение лжи. (По определению следования в ФЛВ).
(6) Существует такая оценка ФЯЛВ, при котором &- объединение А1&…&An формул А1,…,Аn в ФЯЛВ принимает значение истины, а значение В принимает значение лжи. (Из (5) и по таблице для &).
(7) Существует такая оценка ФЯЛВ, при которой значение (А1&…&An Ↄ B) есть ложь. (Из (6) и по таблице для Ↄ)
(8) (А1&…&An Ↄ B) не является законом ФЛВ (Из (7) по опред. закона ФЛВ).
Из (2) и (7) получаем противоречие. Это и есть неприятность. Следовательно, допущение неверно.
Тогда верно, что Т2.
Т2 доказана.
Следствие из Т1 и Т2.
Если (А1,…,Аn, В) есть формулы в ФЯЛВ, то умозаключение А1,…,Аn->В является правильным в ФЛВ тогда и только тогда, когда (А1&…&An Ↄ B) есть закон ФЛВ.
Правильные и неправильные умозаключения в логике высказываний.
Умозаключение - форма мышления, посредством которой из одного и более суждений выводится новое суждение.
Правильное умозаключение называется правильным если в логике высказываний его заключение следует в логике высказываний из множества его посылок.
Неправильное умозаключение называется неправильным если в логике высказываний его заключение не следует в логике высказываний из множества его посылок.
7. Определение закона логики высказываний, примеры закона логики высказываний.
Логический закон - это такая логическая формула высказывания, которая принимает значение "истина" при любой интерпретации параметров, входящих в её состав.
Закон в ФЛВ - формула в ФЯЛВ, которая принимает значение И при всякой оценке ФЯЛВ.
8. Связь правильных умозаключений с законами логики (на примере формальной логики высказываний).
Умозаключением в логике высказываний называется последовательность высказываний, содержащая более одного члена, вместе с утверждением, что последнее из высказываний этой последовательности следует в логике высказываний из множества всех предшествующих ему высказываний в этой последовательности.
Умозаключение является неправильным, если его заключение не следует в логике высказываний из множества его посылок.
Умозаключение называется правильным, если его заключение следует в логике высказываний из множества всех его посылок.
9. Исходные понятия теории множеств.
Множество- любая совокупность, группа, класс произвольных объектов. Множество обозначают заглавными буквами латинского алфавита.
Элемент множества- тот объект, из которого множество состоит.
Принадлежность- отношение между элементом множества и самим множеством.
10. Отношения между множествами.
Отношение включения. Множество А включается во множество В, если всякий элемент множества А является элементом множества В. (А 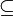 В) В)
Отношение равенства. Множество А= множеству В, если А 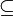 В и В В и В 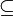 А. Они равны, когда состоят из одних и тех же элементов (множество всех мужчин= множество всех сыновей) А. Они равны, когда состоят из одних и тех же элементов (множество всех мужчин= множество всех сыновей)
Отношение совместимости.
Множество А совместимо с множеством В, если существует такой элемент множества А, который является элементом множества В. (множество всех студентов совместимо с множеством всех Москвичей. Множество всех учителей совместимо с множеством всех блондинов).
Отношение несовместимости.
Множество А несовместимо с множеством В, если ни один элемент множества А не является элементом множества В. (множество родившихся в Москве и множество родившихся в Питере. Множество младенцев и множество студентов).
11. Специальные множества.
Пустое множество.
Множество называется пустым, когда ему не принадлежит ни один элемент. (Множество круглых квадратов, множество людей возрастом более 6000 лет).
Пустое множество включается в любое множество.
Доказательство.
(1) Неверно, что пустое множество включается в любое множество (допущение).
(2) Значит, существует такое множество, куда пустое множество не включается (из (1)).
(3) Пустому множеству принадлежат такие элементы, которые не принадлежат множеству А. (По опред. включения и из (2)).
(4) Значит, некоторые элементы принадлежат пустому множеству.
(5) По определению пустого множество таких элементов быть не может. Противоречие.
Значит, допущение неверно.
Таким образом, пустое множество включается в любое множество.
Пустое множество единственно: если А и В- пустые множества, то они равны.
Доказательство.
(1) А и В- пустые множества (допущение).
(2) А 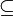 В (из (1), так как А- пустое, оно включается в любое множество, в частности, в В). В (из (1), так как А- пустое, оно включается в любое множество, в частности, в В).
(3) В 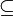 А (т.к В- пустое множество, оно включается в А). А (т.к В- пустое множество, оно включается в А).
(4) А у нас определение, что А=В, когда А 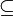 В и В В и В 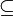 А А
Значит, А=В (из (2) и (3) по опред. равенства множеств).
Семейство множеств.
Множество называется семейством множеств, если всякий его элемент является множеством.
Семейство множеств- множество, каждый элемент которого является множеством.
Универсальное множество.
Множество называется универсальным для данного семейства множеств, если в него включается всякое множество, принадлежащее данному семейству. Универсальное множество обозначается буквой U. Каждое семейство множеств имеет универсальное множество. Универсальное множество всех наций- человечество.
Синглетоны.
Синглетон- одноэлементное множество, т.е множество, которому принадлежит всего 1 элемент. Например, множество всех звезд нашей солнечной системы (в солнечной системе только 1 звезда- Солнце), множество всех президентов СССР (Горбачев только), множество всех столиц РФ (Москва).
12. Операции над множествами.
Пересечение множеств. Пересечением множества А с множеством В называется множество, которому принадлежат все те и только те объекты, каждый из которых принадлежит множеству А и множеству В. Примеры:
| Множества
| Их пересечение
| | Множество всех студентов. Множество всех людей, проживающих в Москве.
| Множество всех студентов, проживающих в Москве.
| | Множество всех мужчин. Множество всех сыновей.
| Множество всех мужчин ИЛИ множество всех сыновей.
| | Множество всех мужчин. Множество всех отцов.
| Множество всех отцов.
| | Множество всех людей, родившихся в Лондоне. Множество всех людей, родившихся в Париже.
| Пустое множество.
|
Объединение множеств. Объединением множества А с множеством В называется множество, которому принадлежат все те и только те объекты, каждый из которых принадлежит хотя бы одному из этих множеств А или В.
| Множество
| Их объединение
| | Множество всех отрицательных целых чисел. Множество всех положительных целых чисел.
| Множество всех целых чисел, исключая ноль.
| | Множество всех отрицательных целых чисел. Множество всех неотрицательных целых чисел.
| Множество всех целых чисел.
| | Множество всех мужчин. Множество всех женщин.
| Множество всех людей.
| | Множество всех англичан. Множество всех блондинов.
| Множество всех людей, которые являются англичанами или блондинами.
|
Разность множеств.
Операция вычитания множеств. Разность множества А с множеством В называется множество, которому принадлежат все те и только те элементы, каждый из которых принадлежит множеству А и не принадлежит множеству В.
| Множества
| А\В
| | Множество всех людей. Множество всех дочерей.
| Множество всех сыновей.
| | Множество всех сыновей. Множество всех людей.
| Пустое множество.
| | Множество всех англичан. Множество всех французов.
| Множество всех англичан
| | Множество всех мужчин. Множество всех женщин.
| Множество всех мужчин.
|
Дополнение до универсального множества.
Дополнением множества А до универсального множества U называется разность U с А (U\A)
| Множество А
| Универсальное множество U
| Дополнение к А до U.
| | Множество всех мужчин.
| Множество всех людей.
| Множество всех женщин.
| | Множество всех матерей.
| Множество всех женщин.
| Множество всех женщин, ни одна из которых не является матерью.
| | Множество всех хвойных лесов.
| Множество всех лесов.
| Множество всех не- хвойных лесов.
| | Множество всех мужчин.
| Множество всех живых существ.
| Множество всех живых существ, исключая мужчин.
|
О символическом изображении дополнения.
Когда универсальное множество зафиксировано и единственно, дополнением до универсального множества обозначается Ᾱ.
13. Диаграммы Эйлера.
Диаграммы Эйлера предназначены для того, чтобы:
1) Графически, наглядно иллюстрировать отношения между множествами
2) Графически, наглядно изображать результаты применения операций между множествами.
Отношение включения.
Когда множество А включается в множество В.
Отношение равенства.
Множество А= множеству В, когда А 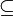 В и В В и В 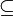 А. А.
Отношение совместимости.
Множество А совместимо с множеством В, если есть такой объект, который принадлежит множеству А и множеству В.
Отношение несовместимости.
Множество А несовместимо с множеством В, когда у них нет общих точек.
14. Определение понятий и примеры понятий.
Понятие- мысль, посредством которой выделяется множество М объектов, на основе такого множества П (признак), что выполняется следующее условие:
х 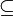 М тогда и только тогда, когда х обладает всеми признаками из П. М тогда и только тогда, когда х обладает всеми признаками из П.
Понятие выражается с помощью существительных и описаний.
Основные логические характеристики понятия- объем и содержание понятия.
Объем понятия- множество всех тех объектов, которые выделяются посредством данного понятия. Содержанием понятия называется множество всех тех признаков, на основе которых выделяется объем понятия.
Отношения между объемами понятий.
Поскольку объемы понятий являются множествами, то отношения между ними те же, что между множествами.
Отношения между содержаниями понятий.
Поскольку содержания понятий являются множествами, то и отношения между ними являются множествами.
15. Основные логические характеристики понятия: объем понятия и содержание понятия.
П1, П2- понятия.
С (П1), С (П2)- содержание
О(П1), О(П2)- объем
Если С (П1) включается в С (П2), то О(П2) включается в О(П1).
Объем понятия «П»- это множество всех П. Иначе говоря, объем понятия «студент»- это множество всех студентов.
Классификация понятий.
Понятия классифицируются по объему:
Общее- если его объему принадлежит более одного элемента.
Единичное- если его объему принадлежит только один элемент.
Пустое- если его объему не принадлежит ни одного элемента.
|



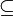 В)
В)


