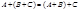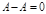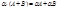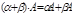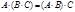Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование поведения функций и их графикиСтр 1 из 2Следующая ⇒
ДИФФиринциал Производная функции f(x) есть некоторая функция f ’(x), произведенная из данной функции.Функция y=f(x), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой в этом интервале. Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Рассмотрим функцию, заданную параметрически: x = φ(t), y = ψ(t). Покажем, что для нахождения производной y'x, совсем необязательно находить выражение явной зависимости y от x. Теорема 12. Пусть функция x = φ(t) имеет обратную функцию t = Ф(x). Если функции x=φ(t), y = ψ(t) дифференцируемы и φ'(t) ≠ 0, тогда Диффиринциал Производной функции γ=f(x) называется функция f'(x), равная пределу отношения приращения функции f(x) к приращению аргумента, когда последнее произвольным образом стремится к нулю:
где?х - приращение аргумента х. Производная функция у обозначается также через у' и Если функция γ=f(x) изображается кривой в декартовых координатах, то γ' при рассматриваемом значении аргумента выражает угловой коэффициент касательной к кривой в соответствующей точке, т. е. γ'=tg α, где α - угол наклона касательной к оси X. Производная имеет не только геометрическое толкование, она выражает скорость изменения функции относительно аргумента, например скорость движения, интенсивность нагрузки, силу тока, теплоемкость и т. п. Если функция имеет в рассматриваемой точке производную, то она в этой точке непрерывна; таким образом, непрерывность является необходимым условием существования производной, но это условие не является достаточным, так как непрерывность не гарантирует существования производной. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции. Обозначается dy или df(x).Из определения следует, что dy = f¢(x)Dx или dy = f¢(x)dx. Можно также записать: Замечательные пределы 1) 2)
Интегрирование тригонометрических выражений
Рассмотрим некоторые случаи нахождения интеграла от тригонометрических функций. Функцию с переменными sin x и cos x, над которыми выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать R(sin x;cos x), где R - знак рациональной функции. Вычисление неопределенных интегралов типа
где R1(t) - рациональная функция от t. Сумма (разность) матриц. Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц. cij = aij ± bij Обозначение: С = А + В = В + А. Умножение матрицы на число. Операция умножения матрицы любого размера на произвольное число сводится к умножению каждого элемента матрицы на это число.
Свойства: a (А±В) =aА ± aВ А(a±b) = aА ± bА Пример: Даны матрицы А = Произведение двух матриц. Замечание: Операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй. В противном случае произведение матриц не определено. Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:Обозначение: A×B = C; Из приведенного определения видно, что каждый элемент матрицы С равен алгебраической сумме произведений элементов i – той строки матрицы А на соответствующие элементы j – го столбца матрицы В. Свойства: 1) Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Транспонирование матриц Определение. Матрицу АТ называют транспонированной матрицей А, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы АТ.(т.е. строки матрицы А заменены на столбцы и наоборот)
А = Замена переменной Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме. Если функция f(z) непрерывна на [a, b], функция z =g (x) имеет на [a,b] непрерывную производную и α ≤ g(x) ≤ β, то ∫ f(g(x)) g' (x) dx = ∫f(z) dz, (8.3) причем после интегрирования в правой части следует сделать подстановку z=g(x). Для доказательства достаточно записать исходный интеграл в виде: ∫ f(g(x)) g (x) dx = ∫ f(g(x)) dg(x). Например: 1) 2) Определённый интеграл I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
V. Постоянный множитель можно выносить за знак определенного интеграла.
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x), вычислить ее значения в точках a и b и найти разность F(b) – F(a). Определенный интеграл был введен для ограниченных на отрезке функций. Естественно распространить это понятие на случай бесконечных промежутков и бесконечно больших функций. Пусть f (x) определена при x ≥ a и интегрируема на отрезке [ a; ξ], где ξ ≥ a. Если существует конечный предел
Если Аналогично определяется несобственный интеграл Операционное исчисление
(f - оригинал; F - изображение). Запись
1. 2. f - кусочно-непрерывна на R. 3.
Если
Если
Если Дифференцирование оригинала
Если
Если
Если
Если
Если
Если
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
1) эллипсоиды
2) гиперболоиды:
3) параболоиды (p > 0, q > 0):
4) конусы второго порядка:
5) цилиндры второго порядка:
Если существует предел
Неопределенности вида 0∙∞; ∞-∞; 1∞; ∞0; 00 сводятся к двум основным. Например, 0∙∞ Пусть f(x)→0, φ(x)→∞ при х→х0
Различные уравнения прямой Всякое уравнение первой степени относительно координат x, y, z Ax + By + Cz +D = 0 2) двумя своими точками M1(x1, y1, z1) и M2(x2, y2, z2), тогда прямая, через них проходящая, задается уравнениями: 3) точкой M1(x1, y1, z1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями: Уравнения (3.4) называются каноническими уравнениями прямой. Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: x = x1 +mt, y = y1 + nt, z = z1 + рt. Теория Каноническим уравнением прямой в пространстве, проходящей через точку A(x0,y0,z0) параллельно вектору a(l,m,n) называется равенство:
Уравнением прямой в пространстве, проходящей через две точки A(x0,y0,z0) и B(x1,y1,z1) называется равенство:
Параметрическим уравнением прямой в пространстве, проходящей через точку A(x0,y0,z0) параллельно вектору a(l,m,n) называется:
РАСТОЯНИЕ ОТ ТОЧКИ.Расстояние d от точки М0 до плоскости ∆ равно модулю проекции вектора
!!!Если плоскость задана уравнением:
то расстояние до плоскости находится по формуле:
УРАВНЕИЕ плоскости Общее уравнение плоскости.
· Если D=0, то данному уравнению удовлетворяет точка О (0;0;0) · Если С=0 то вектор · Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz. Аналогично при A=D=0 и B=D=0. · Если А=В=0 то уравнение примет вид · Если A=B=D=0, то уравнение имеет вид Уравнение плоскости, проходящей через три точки К (х1;у1) М (х2;у2) N (x3;y3) Возьмем на плоскости точку P (x;y;z). Составим векторы:
Эти векторы лежат в одной плоскости, следовательно они компланарны:
Уравнение плоскости в отрезках. Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:
; Нормальное уравнение плоскости.
Углы Угол между прямыми. Дано: прямые L1 и L2 с угловыми коэффициентами
Требуется найти угол между прямыми:
Прямая L: Пусть φ – угол между плоскостью и прямой. Тогда θ – угол между
Найдем
ДИФФиринциал Производная функции f(x) есть некоторая функция f ’(x), произведенная из данной функции.Функция y=f(x), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой в этом интервале. Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Рассмотрим функцию, заданную параметрически: x = φ(t), y = ψ(t). Покажем, что для нахождения производной y'x, совсем необязательно находить выражение явной зависимости y от x. Теорема 12. Пусть функция x = φ(t) имеет обратную функцию t = Ф(x). Если функции x=φ(t), y = ψ(t) дифференцируемы и φ'(t) ≠ 0, тогда Диффиринциал Производной функции γ=f(x) называется функция f'(x), равная пределу отношения приращения функции f(x) к приращению аргумента, когда последнее произвольным образом стремится к нулю:
где?х - приращение аргумента х. Производная функция у обозначается также через у' и Если функция γ=f(x) изображается кривой в декартовых координатах, то γ' при рассматриваемом значении аргумента выражает угловой коэффициент касательной к кривой в соответствующей точке, т. е. γ'=tg α, где α - угол наклона касательной к оси X. Производная имеет не только геометрическое толкование, она выражает скорость изменения функции относительно аргумента, например скорость движения, интенсивность нагрузки, силу тока, теплоемкость и т. п. Если функция имеет в рассматриваемой точке производную, то она в этой точке непрерывна; таким образом, непрерывность является необходимым условием существования производной, но это условие не является достаточным, так как непрерывность не гарантирует существования производной. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции. Обозначается dy или df(x).Из определения следует, что dy = f¢(x)Dx или dy = f¢(x)dx. Можно также записать: Замечательные пределы 1) 2)
Интегрирование тригонометрических выражений
Рассмотрим некоторые случаи нахождения интеграла от тригонометрических функций. Функцию с переменными sin x и cos x, над которыми выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать R(sin x;cos x), где R - знак рациональной функции. Вычисление неопределенных интегралов типа
где R1(t) - рациональная функция от t. Исследование поведения функций и их графики При решении этой задачи находят: 1) область определения функции; 2) точки разрыва и исследуют поведение функции в граничных точках области определения; 3) находят нули функции и промежутки ее знакопостоянства; 4) находят асимптоты; 5) критические точки и интервалы монотонности; 6) точки перегиба и интервалы выпуклости. Замечание. Если функция f (x) четная, т.е. f (x) = f (–x), или нечетная, т.е. f (x) = – f (–x), то исследование функции достаточно провести для x³0, а затем по свойству четности или нечетности построить график при x<0. Завершают исследование функции построением ее графика. Матрицы Матрицей называется прямоугольная таблица чисел, сод Матрица, у которой число строк и столбцов равно – называется квадратной. Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной. Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной. Обозначается буквой Е. Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной. Матрица, у которой все элементы равны нулю, называется нулевой. 1. 2. 3. 4. 5. 6. 7. 8. Операция умножения возможна, если количество столбцов первой матрицы равно количеству строк другой матрицы.
где 1. 2. 3. 4.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.172.249 (0.116 с.) |
 .
. :
: 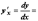




 ; (Первый замечательный предел)
; (Первый замечательный предел) (Второй замечательный предел)Данный предел относят обычно к неопределенностям вида 1∞. Раскрытие подобных неопределенностей как правило, связано с использованием второго замечательного предела.
(Второй замечательный предел)Данный предел относят обычно к неопределенностям вида 1∞. Раскрытие подобных неопределенностей как правило, связано с использованием второго замечательного предела. сводится к вычислению интегралов от paциoнaльнoй фyнкции подстановкой
сводится к вычислению интегралов от paциoнaльнoй фyнкции подстановкой  , которая называется универсальной. Действительно,
, которая называется универсальной. Действительно, ,
, Поэтому
Поэтому
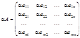
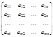 ; АТ=
; АТ=  ;
; ;
;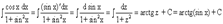 .
. , где х, t – любые буквы.
, где х, t – любые буквы.


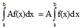


 то говорят, что функция f интегрируема в несобственном смысле на промежутке [ a; +∞), а несобственный интеграл
то говорят, что функция f интегрируема в несобственном смысле на промежутке [ a; +∞), а несобственный интеграл  сходится:
сходится:
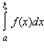 не имеет конечного предела при ξ → +∞, то говорят, что несобственный интеграл расходится.
не имеет конечного предела при ξ → +∞, то говорят, что несобственный интеграл расходится.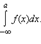



 такие, что
такие, что 

 то
то 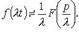
 то
то 
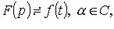 то
то 
 - оригинал, то
- оригинал, то
 - оригинал, то
- оригинал, то
 то
то 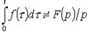
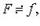 то
то - оригинал, то
- оригинал, то 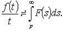
 то
то

 — эллипсоиды,
— эллипсоиды, — мнимые эллипсоиды;
— мнимые эллипсоиды;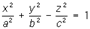 — однополостные гиперболоиды,
— однополостные гиперболоиды,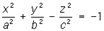 — двуполостные гиперболоиды;
— двуполостные гиперболоиды; — эллиптические параболоиды,
— эллиптические параболоиды, — гиперболические параболоиды;
— гиперболические параболоиды; — конусы,
— конусы, — мнимые конусы;
— мнимые конусы; — эллиптические цилиндры,
— эллиптические цилиндры, — мнимые эллиптические цилиндры,
— мнимые эллиптические цилиндры, — гиперболические цилиндры,
— гиперболические цилиндры, — параболические цилиндры.
— параболические цилиндры.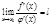 , то
, то 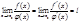
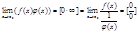

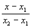 =
=  ; (3.3)
; (3.3) . (3.4)
. (3.4)

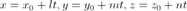
 (где М1(x1;y1;z1) - произвольная точка плоскости) на направление нормального вектора
(где М1(x1;y1;z1) - произвольная точка плоскости) на направление нормального вектора 




 Расстояние d от точки M0(x0,y0,z0)до прямой Аx+By+C=0 вычисляется по формуле:
Расстояние d от точки M0(x0,y0,z0)до прямой Аx+By+C=0 вычисляется по формуле:

 . Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то ox.
. Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то ox.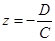 плоскость параллельна плоскости Oxy.
плоскость параллельна плоскости Oxy. . Это уравнение плоскости Oxy.
. Это уравнение плоскости Oxy.

 ;
; 

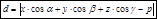




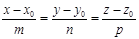
 и
и  .
.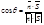
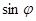 , если
, если 
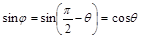 , т.к.
, т.к. 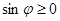


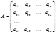 ержащая m строк одинаковой длины.Матрицы равны между собой, если равны все их соответствующие элементы.
ержащая m строк одинаковой длины.Матрицы равны между собой, если равны все их соответствующие элементы.