
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. Экспериментальный раздел работы.
Пример 1. Пусть задано натуральное число m. Необходимо найти минимальное число n такое, что факториал n! > m. По определению, n!=1*2*3*…n.Таким образом, решение поставленной задачи сводится к последовательному увеличению значения n, вычисления n! и сравнения его с заданным числом m. Как только величина n! станет больше m, вычисления
В этой последовательности первый член равен 1, а каждый последующий равен предыдущему, умноженному на k. Такое соотношение называется рекуррентным, что означает «возвращающийся». Из школьного курса математики нам известны такого рода соотношения для членов арифметической Запишем алгоритм нашей задачи: 1. «подготовка» цикла: ввод m; k=1; p=1; 2. «управление» циклом: если p<m, то выполнять пункт 3 (тело цикла), иначе выполнять пункт 4 (вывод результата); 3. «тело» цикла: к=к+1; p=p*k; возврат к пункту 2; 4. вывод результата n=k. Оформим его в виде подпрограммы-функции:
program Example_71; function Min_N(m:integer):integer; var k,p:integer; begin k:= 1; p:=1; while (p<m) do begin Inc(k); p:=p*k end; Min_N:=k end; var m: integer; Begin Writeln(‘Введите число m=?’); readln(m); Writeln(‘ Минимальное значение n=’, Min_N(m)); readln; End.
Провести отладку и тестирование программы. Вычислить значение n для случаев, когда m=MaxInt и MaxLongInt.
Пример 2. Составим программу вычисления степенной функции По определению,
Запишем алгоритм вычислений: 1. «подготовка» цикла: ввод n,x; k=1; y=1; 2. «управление» циклом: если k≤n, то выполнять пункт 3 (тело цикла), иначе выполнять пункт 4 (вывод результата); 3. «тело» цикла: к=к+1; y=y*x; возврат к пункту 2; 4. вывод результата y. Оформим его в виде подпрограммы-функции:
function Pow_1(n:integer; x:real):real; var k:integer; y:real; begin k:= 1; y:=1; while (k<=n) do begin Inc(k); y:=y*x end; Pow_1:=y end;
Проведите отладку и тестирование программы. Попытаемся улучшить составленный алгоритм. В нем нужно было выполнить n операций умножения. Заметим, что, например,
т.е. для четного n=2*k можно, за счет последовательного применения операций возведения в квадрат, уменьшить число умножений до величины k. Если n=2*k+1, то
function Pow_2 (n:integer; x:real): real; var y:real; b:boolean; begin b:= true; y:=1; while b do begin if Odd(n) then y:=y*x; n:=n div 2; if n>0 then x:=x*x else b:=false end; Pow_2:=y end;
Здесь введена логическая переменная b, условие n mod 2 =1 заменено логической функцией Odd(n). Необходимо выполнить тестирование программы и сделать сравнение количества операций двух вариантов программ. Запишем искомую функцию в виде:
где u=1, если n – четно и u=x, если n нечетно. Это позволяет составить еще один вариант программы:
function Pow_3 (n:integer; x:real): real; var u:real; begin if Odd(n) then u:=x else u:=1; if n=1 then Pow_3:=x else Pow_3:=u*sqr(Pow_3(n div 2,x)) end;
Здесь функция Pow_3 вызывает саму себя. Такой прием в программировании называется рекурсивным, но о нем речь пойдем позже. Поэкспериментируйте с разными вариантами программ. Из процесса работы над этим примером можно сделать очень важный вывод: написав программу – поэкспериментируй с ней; поэкспериментировав, - снова вернись к разработке алгоритма и подумай, как его можно улучшить. Параметры улучшения могут быть связаны с уменьшением количества операций, что приведет к сокращению времени работы программы, с уменьшением объема занимаемой в компьютере памяти, понятностью программы.
Пример 3. Напишем логическую функцию, которая будет возвращать значение true, если натуральное число n простое, и false – в противном случае. Напомним, что натуральное число называется простым, если оно делится без остатка только на единицу и само себя. Очевидно также, что число n – составное, если оно делится хотя бы на одно из чисел 2,3,…,n-1. Таким образом, при n>2 необходимо проверить делимость n на каждое из чисел k=2,3, … n-1. На самом деле, как показано в теории чисел, можно сократить сверху диапазон поиска до целой части корня квадратного из n: Составим программу на языке Turbo Pascal: function Simple (n:integer): boolean; var b:boolean; k,max: integer; begin b:= true; max:=trunc(sqrt(n)) + 1; k:=2; while b and (k<max) do begin if n mod k = 0 then b:=false; Inc(k) end; Simple:= b end;
Поэкспериментируйте с программой.
Пример 4. Используя алгоритм Евклида, составим программу определения наибольшего общего делителя числа a на b: НОД(a,b). Один из вариантов этого алгоритма состоит в том, что необходимо последовательно находить остатки от деления:
a на b: b на
.......................... до тех пор, пока
НОД(a,b) = НОД(b,r1) = НОД(r1,r2) =... = НОД(rn,0) = rn. Например,
НОД(18,12) = НОД(12,6) = НОД(6,0) = 6. Напишем подпрограмму-функцию:
function GCD(a,b:integer):integer; { Greatest Common Divisor –наибольший общий делитель} var r1,r2,r3:integer; begin if a>b then begin r1:=a, r2:=b end else begin r1:=b, r2:=a end; while r2 <> 0 do begin r3:=r1 mod r2; r1:=r2; r2:=r3 end; GCD:=r1 end;
Введите, отладьте и протестируйте программу.
Часть 3
ОПЕРАТОР ЦИКЛА С ПОСТУСЛОВИЕМ
Цель работы: - изучить правила работы с оператором цикла repeat … until; - приобрести навыки составления, отладки и тестирования программ, использующих циклы с постусловием; - закрепить навыки работы в среде Turbo Pascal.
|
||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.198 (0.005 с.) |
 нужно прекратить и вывести результат. Последовательное увеличение n организуем с помощью цикла while…do, а для вычисления факториала числа воспользуемся следующими соотношениями:
нужно прекратить и вывести результат. Последовательное увеличение n организуем с помощью цикла while…do, а для вычисления факториала числа воспользуемся следующими соотношениями:
 и геометрической
и геометрической  прогрессий, где d – разность, q – знаменатель. Рекуррентные соотношения играют важную роль в программировании, т.к. в сочетании с операторами циклов создают мощный вычислительный инструментарий.
прогрессий, где d – разность, q – знаменатель. Рекуррентные соотношения играют важную роль в программировании, т.к. в сочетании с операторами циклов создают мощный вычислительный инструментарий. , где n – целое натуральное число, x – вещественное.
, где n – целое натуральное число, x – вещественное. , т.е. искомая функция может быть вычислена с помощью цикла путем многократного умножения на х:
, т.е. искомая функция может быть вычислена с помощью цикла путем многократного умножения на х:
 , где
, где  ,
,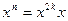 . Запишем новый вариант программы:
. Запишем новый вариант программы: , при n>1 и
, при n>1 и , при n=1,
, при n=1, .
.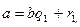 ; r1 = a mod b;
; r1 = a mod b;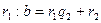 ; r2= b mod r1;
; r2= b mod r1; на
на  ; r3 = r1 mod r2;
; r3 = r1 mod r2; не станет равным нулю. Итак,
не станет равным нулю. Итак,


