
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Невыразимость транзитивного замыкания реляционными операторами
Следующий пример иллюстрирует класс запросов, невыразимых средствами реляционной алгебры или реляционного исчисления по причине невыразимости средствами реляционной алгебры транзитивного замыкания отношений (см. гл. 1). Пример 5.2. Рассмотрим отношение, описывающее сотрудников некоего предприятия. Отношение содержит данные о табельном номере сотрудника, фамилии, должности и табельном номере руководителя сотрудника – СОТРУДНИКИ (ТАБ_НОМ, ФАМИЛИЯ, ДОЛЖНОСТЬ, ТАБ_НОМ_РУК):
Рассмотрим запрос "Перечислить всех руководителей (прямых и непрямых) данного сотрудника". Ответом на запрос может быть получен при помощи понятия транзитивного замыкания. Однако транзитивное замыкание не может быть выражено операторами реляционной алгебры. Определение. Пусть отношение l либо кортеж l либо найдется конечная последовательность элементов Очевидно, что Кросс-таблицы Построение кросс-таблицы средствами реляционной алгебры невозможно, т.к. для этого требуется превратить данные в ячейках таблицы в наименования новых столбцов таблицы. ЛЕКЦИЯ 5. Реляционное исчисление В выражениях реляционной алгебры всегда явно задается некий порядок, а также подразумевается некая стратегия вычисления запроса. В реляционном исчислении не существует никакого описания процедуры вычисления запроса, поскольку в запросе реляционного исчисления указывается, что, а не как следует извлечь. Реляционное исчисление связано с той частью символьной логики, которая называется исчислением предикатов. В контексте баз данных оно существует в двух формах: в форме предложенного Коддом реляционного исчисления кортежей и в форме предложенного Лакруа и Пиро реляционного исчисления доменов. В логике первого порядка (или теории исчисления предикатов) под предикатом подразумевается истинностная функция с параметрами. После подстановки значений вместо параметров функция становится выражением, называемым суждением, которое может быть истинным или ложным. Например, предложения "Иванов является сотрудником данной организации" и "Иванов имеет более высокую зарплату, чем Петрова" являются суждениями, поскольку можно определить их истинность или ложность. В первом случае функция "является сотрудником данной организации" имеет один параметр ("Иванов"), а во втором случае функция "имеет более высокую зарплату, чем" имеет два параметра ("Иванов" и "Петрова").
Если предикат содержит переменную, например в виде "х является сотрудником этой организации", то у этой переменной должна быть соответствующая область определения. При подстановке вместо переменной х одних значений из ее области определения данное суждение может оказаться истинным, а при подстановке других — ложным. Например, если областью определения являются все люди и мы подставим вместо переменной х значение "Иванов", то суждение "Иванов является сотрудником данной организации" будет истинным. Если же вместо переменной х подставить имя другого человека, который не является сотрудником данной организации, то суждение станет ложным. Если Р — предикат, то множество всех значений переменной х, при которых суждение Р становится истинным, можно символически записать следующим образом: {х|Р(х)} Предикаты могут соединяться с помощью логических операций Ù (AND), v (OR) и ~ (NOT) с образованием составных предикатов.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.228.40 (0.006 с.) |
 задано на декартовом квадрате
задано на декартовом квадрате  некоторого множества
некоторого множества  . Транзитивным замыканием отношения
. Транзитивным замыканием отношения 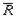 , состоящее из кортежей
, состоящее из кортежей 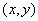 , для которых выполняется:
, для которых выполняется: ,
, , такая, что все кортежи
, такая, что все кортежи 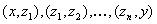 принадлежат отношению
принадлежат отношению  .
.


