
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторные работы ПО гидравликеСодержание книги
Поиск на нашем сайте
Лабораторные работы ПО гидравлике В виртуальной лаборатории
Методические указания
Утверждены редакционно-издательским советом университета 21 января 2009 г.
Самара 2009 Составитель В.И. Веснин
УДК 532; 621.031
Лабораторные работы по гидравлике в виртуальной лаборатории: методические указания / сост. В.И. Веснин; СГАСУ. – Самара, 2009. – 40 с. Методические указания предназначены для студентов дневного и заочного отделений университета специальностей: 290300, 290500, 290700, 290800, 291300, 291500, 330400 при выполнении лабораторных работ по курсу «Гидравлика» (II курс, III-IV семестры очного отделения и IV курс, VII семестр заочного). Приведены необходимые сведения для выполнения лабораторных работ по темам: «Гидростатическое давление и закон Паскаля», «Уравнение Бернулли для установившегося неравномерного движения жидкости», «Режимы течения жидкости», «Гидравлические сопротивления», «Истечение жидкости через малые отверстия в тонкой стенке и насадки при постоянном напоре в атмосферу», «Гидравлический удар». Даются контрольные вопросы к указанным лабораторным работам.
Учебное издание Редактор Г.Ф. Коноплина Технический редактор А.И. Непогодина Корректор Е.М. Исаева
Подписано в печать 20.07.09. Формат 60х84/16. Бумага офсетная. Печать офсетная. Уч.-изд. л. Усл. печ. л. Тираж 100 экз.
Самарский государственный архитектурно-строительный университет 443001 Самара, ул. Молодогвардейская, 194
Общая часть
Компьютерная версия лаборатории гидромеханики предназначена для имитационного выполнения лабораторных работ в соответствии с программой дисциплины «Гидравлика». Она включает в себя одну лабораторную установку по гидростатике и 5 установок по гидродинамике. Виртуальная лаборатория состоит из мультипликационного изображения на экране дисплея действующих установок и математической модели изучаемого физического процесса, управляющей содержанием экрана. Программа позволяет имитировать измерение параметров физического процесса с помощью применяемых в практике гидравлического эксперимента приборов. В процессе компьютерного эксперимента программа воспроизводит случайное отклонение измеряемого параметра, что дает возможность оценить точность измерений методами статистического анализа.
Каждая из лабораторных установок состоит из трех разделов: 1 – схема лабораторной установки, аналогичная приведенной в настоящих методических указаниях; 2 – информация о программе, описывающая методику выполнения данной работы и содержащая необходимые исходные данные, которые частично указываются на схеме; 3 – проведение эксперимента, который ведется в диалоговом режиме компьютера. Программа позволяет проводить эксперимент в различных режимах.
Работа 1 ИЗМЕРЕНИЕ ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ И ЭКСПЕРИМЕНТАЛЬНОЕ ПОДТВЕРЖДЕНИЕ ЗАКОНА ПАСКАЛЯ Цель работы: 1. Освоить технику измерения давления в жидкости с помощью пружинных манометров. 2. Подтвердить на основании опытных данных закон Паскаля. 3. Построить по данным опыта № 2 в масштабе эпюру манометрического давления по глубине Общие сведения Гидростатическим давлением
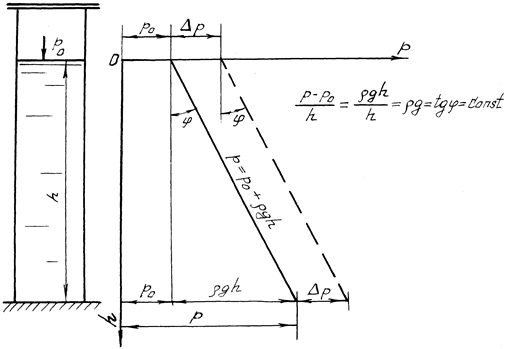
где Δρ- элементарная равнодействующая поверхностных и массовых сил (гидростатическая сила), Н; Δω- элементарная площадка действия, м2. Из формулы (1.1) видно, что гидростатическое давление За единицу гидростатического давления принято равномерно распределённое давление, создаваемое силой в 1 Н на площади в 1 м2, т.е. Гидростатическое давление, отсчитываемое от нуля, называют абсолютным (
Очевидно,
Величину нормального атмосферного давления Из формулы (1.3) видно, что в зависимости от соотношения между
По принципу действия манометры и вакуумметры делятся на две группы: жидкостные и механические. Жидкостный манометр (пьезометр) представляет собой стеклянную трубку, верхний конец которой открыт в атмосферу, а нижний присоединён к точке, где измеряется манометрическое давление. Манометрическое давление, выраженное через показания манометра, равно:
где
Действие механических приборов основано на деформации под действием давления упругого элемента (пружины или мембраны). Заметим, что пружинный манометр показывает давление в точке жидкости на уровне оси вращения его стрелки. Если высотное положение оси вращения стрелки и точки подключения манометра не совпадает (рисунок 1.1), в показание манометра ( Для случая, изображённого на рисунке 1.1,
где В данной лабораторной работе предусмотрено измерение манометрического давления пружинными манометрами. Когда на покоящуюся жидкость действует только сила тяжести, распределение гидростатического давления
где
Из уравнения (1.6) видно, что при Из уравнения (1.6) следует, что внешнее давление
Рисунок 1.1 - Схема установки для экспериментального подтверждения закона Паскаля: 1 – металлическая колонна; 2 – водомерное стекло; 3 – мерная шкала в метрах; 4 – механический манометр и его шкала в кПа; 5 – воздушный компрессор
Рисунок 1.2 - К закону Паскаля и его экспериментальному подтверждению Описание установки Установка (рисунок 1.1) представляет собой толстостенный стальной цилиндр 1, частично заполненный водой, уровень которой измеряется водомерной трубкой 2 со шкалой 3. Для изменения гидростатического давления над свободной поверхностью жидкости (в точке А) и в точках В и С, заглублённых под уровень соответственно на В пространство над свободной поверхностью можно подавать сжатый воздух от компрессора 5. В крышке цилиндра имеется предохранительный клапан 2, отрегулированный на давление 500 кПа (на рисунке 1.1 не показан). Общие сведения Для двух произвольно выбранных живых сечений I-I и II-II струйки реальной жидкости (рисунок 2.1) при установившемся движении уравнение Д. Бернулли имеет вид:
Слагаемые, входящие в уравнение (2.1), можно истолковать с геометрической и энергетической точек зрения. С геометрической точки зрения, слагаемые уравнения (2.1) являются высотами (напорами): z - геометрическая высота (напор),т.е. превышение центра тяжести рассматриваемого поперечного сечения струйки над плоскостью сравнения 0-0, выбираемой произвольно (рисунок 2.1); p/rg - пьезометрическая высота, т.е. высота подъема жидкости в пьезометре, подключенном к центру тяжести рассматриваемого сечения струйки, отвечающая гидродинамическому давлению р в этой точке; u2/2g - скоростная высота (напор), отвечающая местной скорости u,
С энергетической точки зрения, слагаемые уравнения (2.1) представляют собой разновидности удельной энергии, а именно: z - удельная потенциальная энергия положения жидкости в рассматриваемом сечении струйки; P/rg - удельная потенциальная энергия давления; u2/2g - удельная кинетическая энергия;
h`w1-2 - потеря полной удельной энергии струйки, т.е. часть ее, затраченная на преодоление работы сил внутреннего трения, обусловленного вязкостью жидкости. Удельной энергией называется энергия, приходящаяся на единицу веса жидкости. Величины слагаемых уравнения (2.1) могут быть определены опытным путем следующим образом: z - геометрическим нивелированием или же измерением линейкой; p/rg - с помощью пьезометрической трубки (пьезометра); u2/2g - по разности отметок уровней жидкости в скоростной и пьезометрической трубках, подключенных к рассматриваемой точке живого сечения струйки (рисунок 2.2); h`w1-2 - по разности отметок уровней воды в скоростных трубках, подключенных к сечениям I-I и II-II (рисунок 2.2).
Рисунок 2.1 – Диаграмма уравнения Д.Бернулли для струйки реальной жидкости
Рисунок 2.2 – Измерение скоростного напора u2/2g: а - напорное движение жидкости; б - безнапорное движение жидкости
Скоростная трубка (рисунок 2.2) представляет собой трубку, верхний конец которой открыт в атмосферу, а нижний изогнут навстречу скорости и в рассматриваемой точке потока жидкости. Благодаря этому у входа в изогнутый конец скоростной трубки кинетическая энергия частицы жидкости преобразуется в потенциальную энергию давления столба жидкости высотой hu= u2/2g.
Поскольку срез нижнего конца скоростной трубки перпендикулярен вектору скорости, а срез нижнего конца пьезометра параллелен (рисунок 2.2), уровень жидкости в скоростной трубке всегда устанавливается выше, чем в пьезометре, на величину u2/2g. Прибор, объединяющий конструктивно пьезометрическую (П) и скоростную (С) трубки, называется трубкой Пито и широко применяется для измерения скорости движения жидкости Для двух сечений потока реальной жидкости уравнение Д. Бернулли имеет вид:
где hw1-2 - потеря полного напора (полной удельной энергии) на преодоление работы сил внутреннего и внешнего трения на пути между живыми сечениями потока жидкости I-I и II-II; a - коэффициент Кориолиса (корректив кинетической энергии), учитывающий неравномерность распределения местных скоростей Величина a зависит от режима течения жидкости, а также от вида движения. Так, при равномерном движении для ламинарного режима a=2,0, а для турбулентного - a=1,05…1,15. Слагаемые уравнений (2.1) и (2.2) в различных живых сечениях можно изображать графически в виде диаграммы уравнения Д. Бернулли (графика напоров), рисунок 2.1, дающей наглядное представление о перераспределении по пути движения жидкости потенциальной и кинетической энергии, а также о характере убывания полной энергии. Описание установки Установка (рисунок 2.3) представляет собой трубопровод 2 переменного сечения с напорным баком 1, вода в который подается по питающему трубопроводу 8. Бак 1 снабжен переливным устройством 10 для поддержания уровня воды на постоянной отметке, чтобы обеспечить в трубопроводе 2 установившееся движение жидкости. К сечениям I-I…II-II трубопровода 2 подключены пьезометры 3 и скоростные трубки 4 для измерения величин p/rg и u2/2g. Расход воды в трубопроводе 2 регулируется вентилем 6. Для измерения расхода воды имеются мерный бак 7 и секундомер 5.
Рисунок 2.3 – Схема установки: 1 – напорный питающий бак; 2 – трубопровод переменного сечения; 3 – пьезометры; 4 – скоростные трубки; 5 – секундомер; 6 – вентиль для регулирования расхода воды; 7 – мерный бак; 8 – питающий трубопровод; 9 – переливное устройство Общие сведения Многочисленными экспериментальными исследованиями установлено, что движение жидкости может происходить или при ламинарном, или при турбулентном режиме. Ламинарный режим наблюдается при небольших скоростях движения. При этом окрашенные струйки жидкости не перемешиваются, сохраняясь по всей длине потока, т.е. движение жидкости при ламинарном режиме является струйчатым, перемешивание частиц жидкости отсутствует. Турбулентный режим наблюдается при значительных скоростях и характеризуется интенсивным перемешиванием частиц жидкости, что обусловливает пульсацию скоростей и давления.
Средняя скорость потока, при которой происходит смена режима движения жидкости, называется критической (
от m, r и d не зависит. Reкр(d)=2320 называется критическим числом Рейнольдса. Устойчивый ламинарный режим наблюдается при значениях числа Рейнольдса Таким образом, число Рейнольдса
является критерием, позволяющим судить о режиме движения жидкости в круглой трубе, работающей полным сечением. Величину n=m/r, входящую в формулы (3.1) и (3.2), называют кинематическим коэффициентом вязкости жидкости. Из изложенного следует, что для определения режима движения жидкости в круглом трубопроводе при напорном движении достаточно вычислить по формуле (3.2) число Рейнольдса и сравнить его с критическим. Знание режима движения жидкости необходимо для правильной оценки потерь напора при гидравлических расчетах. Дело в том, что зависимость потерь напора по длине he от средней скорости
Рисунок 3.1 – График зависимости потерь напора по длине hℓ от средней скорости υ в логарифмической форме
При ламинарном режиме потери напора he пропорциональны средней скорости 3.2 Описание установки (рисунок 3.2) Включает в себя стеклянную трубу расположенную горизонтально 2, в которой изучается движение воды при различных режимах, напорный бак 1, емкость 6 с раствором красителя, подаваемого по капиллярной трубке во входное сечение трубы 2. Для измерения расхода воды в трубе 2 служат мерная емкость 5 и секундомер 7. Вода в напорный бак 3 подается по питающему трубопроводу из резервуара лаборатории. Для поддержания уровня воды в баке 1 во время опытов на постоянной отметке имеется переливное устройство.
Рисунок 3.2 – Схема установки: 1 – напорный бак; 2 – стеклянная прозрачная трубка; 3 – пьезометры; 4 – регулирующий кран; 5 – мерный бак; 6 – водный краситель; 7 – секундомер; 8 – индикация разности уровней в пьезометрах (гидравлических потерь)
Регулирование расхода воды, а следовательно, и средней скорости ее движения в трубе 2, осуществляется краном. На трубе 2 имеются пьезометры 3 для определения потерь напора по длине hℓ (по разности их показаний). И МЕСТНЫХ СОПРОТИВЛЕНИЙ
Цель работы: 1. Определить по опытным данным, воспользовавшись формулами (4.2) и (4.3), значение коэффициента гидравлического трения 2. Установить, воспользовавшись соотношениями А.Н. Альтшуля или же графиком Никурадзе (рисунок 4.1), области гидравлического сопротивления, в которых работали участки напорного трубопровода. 3. Вычислить значения коэффициентов гидравлического трения 4. Найти справочные значения коэффициентов местных сопротивлений ( 5. Оценить сходимость
Общие сведения Экспериментальными исследованиями установлено, что при движении жидкости часть полного напора (энергии) затрачивается на преодоление работы вязкостных и инерциональных сил, т.е. возникают потери напора. При равномерном движении жидкости гидравлическое сопротивление, проявляющееся равномерно по всей длине потока, называют сопротивлением по длине, а вызываемые им потери напора - потерями напора по длине (hℓ). Эти потери в круглых трубопроводах, работающих полным сечением, вычисляют по формуле Дарси-Вейсбаха:
где l - безразмерный коэффициент, называемый коэффициентом гидравлического трения (коэффициентом Дарси). Величина коэффициента l характеризует гидравлическое сопротивление трубопровода и зависит в общем случае от числа Рейнольдса Re и относительной шероховатости Dэ/d трубопровода, т.е. l=f(Re, Dэ/d); l, d – длина и внутренний диаметр трубопровода;
Величину коэффициента l при гидравлических экспериментах вычисляют по опытным данным из формулы (4.1). При гидравлических же расчетах – по эмпирическим и полуэмпирическим формулам, например, при ламинарном режиме lп=64/Rе, а при турбулентном режиме движения и работе трубопровода в области доквадратичного сопротивления – по формуле А.Д. Альтшуля:
Величину абсолютной эквивалентной шероховатости Dэ при расчетах берут из справочной литературы в зависимости от материала трубопровода и состояния его внутренней поверхности. Например, для труб из органического стекла Dэ=0,006 мм, а для стальных водопроводных умеренно заржавленных труб Dэ=0,20…0,50 мм. Область гидравлического сопротивления при расчетах определяют или непосредственно по графикам l=f(Re,Dэ/d), полученным опытным путем для труб из различных материалов и приведенным в справочной литературе, например, по графику Никурадзе (рисунке 4.1), или же с помощью соотношений
Вычисляют соотношения 10d/Dэ и 500d/Dэ и сравнивают их с числом Рейнольдса Re = Vd/n. При этом, если
Следует иметь в виду, что для каждой области гидравлического сопротивления предложены и используются при гидравлических расчетах свои формулы для вычисления коэффициента l. Другой вид гидравлических сопротивлений, возникающих в местах резкого изменения конфигурации потока, называют местными сопротивлениями, а вызываемые ими потери напора - местными потерями напора (hм). При прохождении через любое местное сопротивление поток жидкости деформируется (рисунок 4.2 а, б, в), вследствие чего движение становится неравномерным резко изменяющимся, для которого характерны: а) значительное искривление линий потока и кривых сечений потока; б) отрывы транзитной струи от стенок трубопровода (ввиду действия закона инерции) и возникновения в местах отрыва устойчивых водовязатов; в) повышенная (по сравнению с равномерным движением) пульсация скоростей и давлений; г) изменение формы (переформирование) эпюр скоростей.
Местные потери напора при гидравлических расчетах вычисляют по формуле Вейсбаха:
где
Величина коэффициента Величину
если же скорость берется за местным сопротивлением, т.е.
Коэффициент сопротивления при резком сужении трубопровода (
где
4.2 Описание установки Установка (рисунок 4.3) представляет собой систему напорных трубопроводов с последовательно расположенными на нем гидравлическими сопротивлениями (по длине и местными). К каждому гидравлическому сопротивлению подключено по два пьезометра (перед и за ним). Все пьезометры для удобства работы выведены на щит 4. Для регулирования расхода воды
Рисунок 4.3 – Схема установки: 1 – мерный бак; 2 – вентиль для регулирования расхода воды; 3 – секундомер; 4 – пьезометры; 5 – напорный питающий бак; D1 и D2 – диаметры трубопроводов Общие сведения Малым считаются отверстие, высота которого не превышает 0,1 Н (рисунок 5.1). Здесь Н - превышение свободной поверхности жидкости над центром тяжести отверстия. Стенку считают тонкой, если ее толщина d < (1,5...3,0)d (рисунок 5.1). При выполнении этого условия величина d не влияет на характер истечения жидкости из отверстия, так как вытекающая струя жидкости касается только острой кромки отверстия.
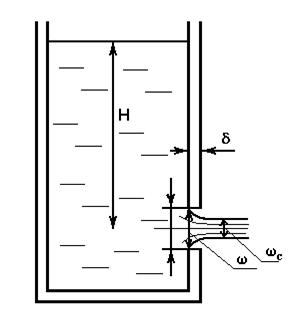
Рисунок 5.1 – Расчетная схема истечения жидкости из малого отверстия в тонкой стенке
Поскольку частицы жидкости движутся к отверстию по криволинейным траекториям сил инерции струя, вытекающая из отверстия, сжимается. Благодаря действию сил инерции струя продолжает сжиматься и после выхода из отверстия. Наибольшее сжатие струи, как показывают опыты, наблюдается в сечении с-с на расстоянии примерно (0,5...1,0)d от входной кромки отверстия (рисунок 5.1). Это сечение называют сжатым. Степень сжатия струи в этом сечении оценивают коэффициентом сжатия e:
где wс и w соответственно площадь сжатого живого сечения струи и площадь отверстия. Среднюю скорость струи Vc в сжатом сечении с-с при р0=рат вычисляют по формуле, полученной из уравнения Д. Бернулли, составленного для сечений I-I и с-с (рисунок 5.1):
где j - коэффициент скорости отверстия.
На основе использования уравнения траектории струи, вытекающей из отверстия, получено еще одно выражение для коэффициента j:
В формулах(5.3) и(5.4) a - коэффициент Кориолиса, z - коэффициент сопротивления отверстия, xi и yi - координаты произвольно взятой точки траектории струи. Поскольку напор теряется главным образом вблизи отверстия, где скорости достаточно велики, при истечении из отверстия во внимание принимают только местные потери напора. Расход жидкости Q через отверстие равен:
где Здесь m - коэффициент расхода отверстия, учитывающий влияние гидравлического сопротивления и сжатия струи на расход жидкости. С учетом выражения для m формула (1.25) принимает вид:
Величины коэффициентов e, z, j, m для отверстий определяют опытным путем. Установлено, что они зависят от формы отверстия и числа Рейнольдса. Однако при больших числах Рейнольдса (Re ³ 105) указанные коэффициенты от Re не зависят и для круглых и квадратных отверстий при совершенном сжатии струи равны: e= 0,62...0,64, z=0,06, j=0,97...0,98, m=0,60...0,62. Насадкой называют патрубок длиной 2,5d £ LH £ 5d, присоединенный к малому отверстию в тонкой стенке с целью изменения гидравлических характеристик истечения (скорости, расхода жидкости, траектории струи). Насадки бывают цилиндрические (внешние и внутренние), конические (сходящиеся и расходящиеся) и коноидальные, т.е. очерченные по форме струи, вытекающей из отверстия. Использование насадки любого типа вызывает увеличение расхода жидкости Q благодаря вакууму, возникающему внутри насадка в области сжатого сечения и обусловливающему повышение напора истечения. Среднюю скорость истечения жидкости из насадки V и расход Q определяют по формулам, полученным из уравнения Д. Бернулли.
Здесь zН - коэффициент сопротивления насадки. Для выходного сечения в-в коэффициент сжатия струи e=1 (насадка в этой области работает полным сечением), поэтому коэффициент расхода насадки mН = jН. Расход жидкости, вытекающей из насадки, вычисляется по формуле, аналогичной (5.7),
Описание установки Установка (рисунок 5.2) представляет собой напорный резервуар 1, в боковой поверхности которого имеется отверстие. Перед отверстием (снаружи резервуара 1) смонтирован поворотный круг с отверстием и насадками различных типов. Поворачивая круг, можно установить против отверстия 3 насадки нужного типа или отверстия. Постоянный уровень воды в резервуаре 1 во время опытов поддерживается переливной трубой, а ослабление возмущений, создаваемых поступающей в него водой, осуществляется успокоительной решеткой. Для определения напора истечения Н резервуар I снабжен водомерной трубкой 6 со шкалой, нуль которой совмещен с центром отверстия. Расход воды при истечении из отверстий и насадков измеряется с помощью передвижного мерного бака 2 и секундомера. Для опорожнения мерного бака имеется вентиль 8. Координаты X и Y произвольных точек траектории струи измеряются с помощью координатной сетки, нанесенной на координатный планшет 4.
Рисунок 5.2 – Схема лабораторной установки: 1 – напорный резервуар; 2 – мерный бак; 3 – водомерное стекло; 4 – координатный планшет; 5 – струя истечения жидкости; 6 – пьезометр; 7 – напор истечения; 8 - секундомер
В НАПОРНОМ ТРУБОПРОВОДЕ
Цель работы: Определить опытным путем величину повышения давления Dроп при прямом гидравлическом ударе в напорном трубопроводе, сравнить ее с величиной Dр, вычисленной по формуле Н. Е. Жуковского, и подсчитать относительное отклонение.
Общие сведения Гидравлическим ударом называется изменение (повышение или понижение) давления в напорном трубопроводе при резком изменении скорости движения жидкости (например, в результате резкого закрытия или открытия затвора). Повышение давления при гидравлическом ударе может быть настолько большим, что способно привести к разрыву трубопровода. При быстром закрытии затвора сначала остановится не вся масса жидкости, заключенная в трубопроводе, а лишь часть ее, находящаяся непосредственно перед затвором (рисунок 6.1). Это происходит благодаря инерции и упругим свойствам жидкости и материала трубы (остановившаяся масса жидкости несколько сжимается, труба расширяется, а давление в жидкости резко возрастает). Затем повышение давления весьма быстро распространяется по трубопроводу от затвора к резервуару. Скорость распространения повышения давления называют
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.241.79 (0.016 с.) |

 .
. называют нормальное сжимающее напряжение, возникающее в покоящейся жидкости под действием поверхностных и массовых сил,
называют нормальное сжимающее напряжение, возникающее в покоящейся жидкости под действием поверхностных и массовых сил, , (1.1)
, (1.1) (один Паскаль).
(один Паскаль). ), а отсчитываемое от атмосферного (
), а отсчитываемое от атмосферного ( ) – избыточным (
) – избыточным ( ), следовательно,
), следовательно, . (1.2)
. (1.2) . (1.3)
. (1.3) , (1.4)
, (1.4) - объемный вес жидкости;
- объемный вес жидкости; - пьезометрическая высота, т.е. высота, отсчитываемая от точки подключения пьезометра до уровня жидкости в нём.
- пьезометрическая высота, т.е. высота, отсчитываемая от точки подключения пьезометра до уровня жидкости в нём. ) вводят поправку (
) вводят поправку ( ).
). , (1.5)
, (1.5) - превышение оси вращения стрелки манометра над точкой его подключения, м.
- превышение оси вращения стрелки манометра над точкой его подключения, м. , (1.6)
, (1.6) - внешнее давление, т.е. гидростатическое давление на свободной поверхности жидкости, Па;
- внешнее давление, т.е. гидростатическое давление на свободной поверхности жидкости, Па; - весовое давление, т.е. гидростатическое давление, создаваемое весом столба
- весовое давление, т.е. гидростатическое давление, создаваемое весом столба  и
и  давление
давление 
 и
и 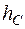 , подключены пружинные манометры
, подключены пружинные манометры 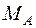 ,
,  ,
,  .
. . (2.1)
. (2.1) - гидростатический напор;
- гидростатический напор; - полный напор в рассматриваемом сечении струйки;
- полный напор в рассматриваемом сечении струйки; - потеря полного напора, т.е. часть полного напора, затраченная на преодоление гидравлических сопротивлений на пути между сечениями I-I и II-II.
- потеря полного напора, т.е. часть полного напора, затраченная на преодоление гидравлических сопротивлений на пути между сечениями I-I и II-II. - полная удельная энергия;
- полная удельная энергия;

 .
. , (2.2)
, (2.2)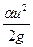 - скоростной напор, отвечающий средней скорости
- скоростной напор, отвечающий средней скорости  потока жидкости в рассматриваемом живом сечении (здесь Q, - расход потока жидкости, w - площадь живого сечения потока);
потока жидкости в рассматриваемом живом сечении (здесь Q, - расход потока жидкости, w - площадь живого сечения потока); по живому сечению потока, обусловленную вязкостью жидкости.
по живому сечению потока, обусловленную вязкостью жидкости.
 (3.1)
(3.1) , а турбулентный – при Re(d)>Reкр(d).
, а турбулентный – при Re(d)>Reкр(d). (3.2)
(3.2)

 и величины коэффициента
и величины коэффициента  для трех видов местных сопротивлений.
для трех видов местных сопротивлений. по соответствующим эмпирическим формулам.
по соответствующим эмпирическим формулам. - по таблице,
- по таблице, 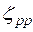 и
и  - по формулам (4.4), (4.6)).
- по формулам (4.4), (4.6)). с их расчетными справочными значениями.
с их расчетными справочными значениями. (4.1)
(4.1) . (4.2)
. (4.2) и
и  , предложенных А. Д. Альтшулем на основе использования упомянутых графиков. В последнем случае поступают следующим образом.
, предложенных А. Д. Альтшулем на основе использования упомянутых графиков. В последнем случае поступают следующим образом.

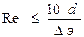 , трубопровод работает в области гидравлически гладких труб. Если
, трубопровод работает в области гидравлически гладких труб. Если  , трубопровод работает в области квадратичного сопротивления. Если же 10d/Dэ ≤ Re ≤ 500dэ/Dэ, трубопровод работает в области доквадратичного сопротивления.
, трубопровод работает в области квадратичного сопротивления. Если же 10d/Dэ ≤ Re ≤ 500dэ/Dэ, трубопровод работает в области доквадратичного сопротивления.
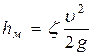 , (4.3)
, (4.3) зависит в общем случае от числа Рейнольдса
зависит в общем случае от числа Рейнольдса 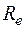 и от конфигурации, т.е. формы проточной части местного сопротивления. В частном случае, когда трубопровод, на котором расположено местное сопротивление, работает в области квадратичного сопротивления, величина коэффициента
и от конфигурации, т.е. формы проточной части местного сопротивления. В частном случае, когда трубопровод, на котором расположено местное сопротивление, работает в области квадратичного сопротивления, величина коэффициента 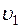 ,
, , (4.4)
, (4.4)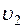 ,
, (4.5)
(4.5) , (4.6)
, (4.6) - коэффициент сжатия струи.
- коэффициент сжатия струи.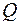 в системе служит вентиль 2. Величина
в системе служит вентиль 2. Величина 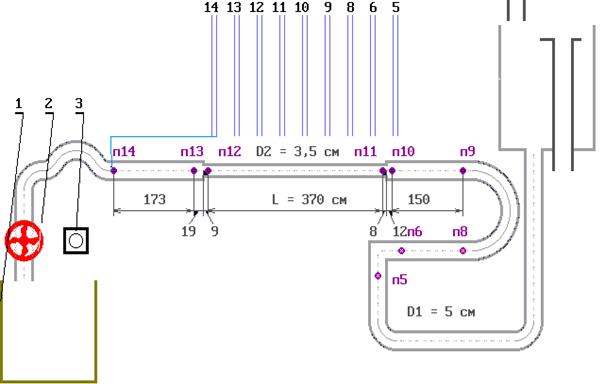
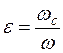 , (5.1)
, (5.1) , (5.2)
, (5.2)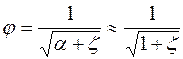 . (5.3)
. (5.3)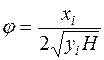 . (5.4)
. (5.4)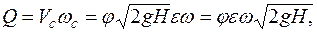 (5.5)
(5.5) . (5.6)
. (5.6) (5.7)
(5.7) . (5.8)
. (5.8) - коэффициент скорости насадки,
- коэффициент скорости насадки, (5.9)
(5.9)



