
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И построение графика давления»
И построение графика давления» Вариант №3
Выполнил: Стародубцев А.О. Группа: НД-10-3 Проверила: Исакова Е.А.
Москва, 2012 г. Содержание: Введение3 Теоретическая часть6 Расчетная часть7 Интервал 1 7 Интервал 2 8 Интервал 3 9 Интервал 5 10 Интервал 6 11 Интервал 7 12 Интервал 8 13 Иные потери давления 14 Расчет давления в точках 15 Графическая часть16 Приложения17 Выводы18 Использованная литература19 Введение Что такое, вообще говоря, жидкость? Жидкость — агрегатное состояние вещества, обладающее свойством, отличающим её от других агрегатных состояний — способность неограниченно менять форму под действием механических напряжений, даже сколь угодно малых, практически сохраняя при этом объём. Это свойство называется текучестью, и именно благодаря нему мы отличаем жидкость от остальных агрегатных состояний. Собственно, жидкость и считается чем-то промежуточным между твердым телом и газом — газ не сохраняет ни объём, ни форму, а твёрдое тело сохраняет и то, и другое. Другое важное свойство жидкостей, роднящее их с газами — это вязкость. Она определяется, как способность оказывать сопротивление перемещению одной из части относительно другой — то есть как внутреннее трение. Когда соседние слои жидкости движутся относительно друг друга, неизбежно происходит столкновение молекул дополнительно к тому, которое обусловлено тепловым движением. Возникают силы, затормаживающие упорядоченное движение. При этом кинетическая энергия упорядоченного движения переходит в тепловую — энергию хаотического движения молекул. Все обладающие вязкостью жидкости подразделяются на ньютоновские и неньютоновские.
где Кривая течения ньютоновских жидкостей, т.е. график зависимости касательного напряжения от градиента скорости, представляет собой прямую линию, выходящую из начала координат, с тангенсом угла наклона η (рис.1, линия 4).
1 — нелинейновязкопластичная, 2 — вязкопластичная, 3 — псевдопластичная, 4 — ньютоновская, 5 — дилатантная.
Ньютоновская вязкость η представляет собой силу трения, приходящуюся на единицу длины площади поверхности при градиенте скорости, равной единице. Она зависит только от температуры и давления и полностью характеризует поведение жидкости. Ньютоновскими, или нормальными характеристиками течения, обладают все газы, жидкости и растворы, имеющие небольшую молекулярную массу (вода, бензин и т. д.). Неньютоновскими, или аномальными, называют жидкости, течение которых не подчиняется закону Ньютона. Таких, аномальных с точки зрения гидравлики, жидкостей немало. Они широко распространены в нефтяной, химической, перерабатывающей и других отраслях промышленности. Все неньютоновские жидкости можно разделить на три группы: 1. Неньютоновские вязкие жидкости. 2. Неньютоновские нереостабильные жидкости. 3. Неньютоновские вязкоупругие жидкости. Неньютоновские вязкие жидкости характеризуются тем, что их свойства не зависят от времени, а касательное напряжение является простой функцией градиента скорости. Они подразделяются на: · вязкопластичные жидкости; · псевдопластичные жидкости; · дилатантные жидкости; · нелинейно-вязкопластичные жидкости.
Если к вязкопластичной жидкости прикладывать напряжение сдвига, меньшим по величине, чем τ0, то такая жидкость будет оставаться в покое. Как только напряжение сдвига превысит τ0 вязкопластик начнет течь, как обычная ньютоновская жидкость. Иначе говоря, привести в движение вязкопластичную жидкость можно, лишь преодолев её статическое (предельное) напряжение — это полностью соответствует уже рассмотренной нами реологической модели Бингама.
Такое поведение вязкопластиков объясняется тем, что в жидкости, находящейся в покое, образуется жесткая пространственная структура, оказывающая сопротивление любому напряжению, меньшему τ0. При напряжениях, больших τ0, структура полностью разрушается и не препятствует движению жидкости. При напряжениях, меньших τ0, структура вновь восстанавливается, а жидкость перестает течь. К вязкопластичным жидкостям можно отнести буровые растворы, сточные грязи, масляные краски, зубную пасту и т. д. Для неньютоновских вязких жидкостей используется понятие кажущейся или эффективной вязкости. Использование эффективной вязкости позволяет приближенно рассчитывать движение аномальных сред по уравнениям и формулам, полученным для ньютоновских жидкостей. Теоретическая часть
Расчетная часть Рис.3 График зависимости давления от длины бурения скважины Приложения
График зависимости безразмерного коэффициента βк, от числа Сен-Венана – Ильюшина: 1 - для труб; 2 - для соосного кольцевого пространства.
Кривая критических значений числа Рейнольдса перехода в турбулентный режим Выводы и построение графика давления» Вариант №3
Выполнил: Стародубцев А.О. Группа: НД-10-3 Проверила: Исакова Е.А.
Москва, 2012 г. Содержание: Введение3 Теоретическая часть6 Расчетная часть7 Интервал 1 7 Интервал 2 8 Интервал 3 9 Интервал 5 10 Интервал 6 11 Интервал 7 12 Интервал 8 13 Иные потери давления 14 Расчет давления в точках 15 Графическая часть16 Приложения17 Выводы18 Использованная литература19 Введение Что такое, вообще говоря, жидкость? Жидкость — агрегатное состояние вещества, обладающее свойством, отличающим её от других агрегатных состояний — способность неограниченно менять форму под действием механических напряжений, даже сколь угодно малых, практически сохраняя при этом объём. Это свойство называется текучестью, и именно благодаря нему мы отличаем жидкость от остальных агрегатных состояний. Собственно, жидкость и считается чем-то промежуточным между твердым телом и газом — газ не сохраняет ни объём, ни форму, а твёрдое тело сохраняет и то, и другое.
Другое важное свойство жидкостей, роднящее их с газами — это вязкость. Она определяется, как способность оказывать сопротивление перемещению одной из части относительно другой — то есть как внутреннее трение. Когда соседние слои жидкости движутся относительно друг друга, неизбежно происходит столкновение молекул дополнительно к тому, которое обусловлено тепловым движением. Возникают силы, затормаживающие упорядоченное движение. При этом кинетическая энергия упорядоченного движения переходит в тепловую — энергию хаотического движения молекул. Все обладающие вязкостью жидкости подразделяются на ньютоновские и неньютоновские.
где Кривая течения ньютоновских жидкостей, т.е. график зависимости касательного напряжения от градиента скорости, представляет собой прямую линию, выходящую из начала координат, с тангенсом угла наклона η (рис.1, линия 4).
1 — нелинейновязкопластичная, 2 — вязкопластичная, 3 — псевдопластичная, 4 — ньютоновская, 5 — дилатантная.
Ньютоновская вязкость η представляет собой силу трения, приходящуюся на единицу длины площади поверхности при градиенте скорости, равной единице. Она зависит только от температуры и давления и полностью характеризует поведение жидкости. Ньютоновскими, или нормальными характеристиками течения, обладают все газы, жидкости и растворы, имеющие небольшую молекулярную массу (вода, бензин и т. д.). Неньютоновскими, или аномальными, называют жидкости, течение которых не подчиняется закону Ньютона. Таких, аномальных с точки зрения гидравлики, жидкостей немало. Они широко распространены в нефтяной, химической, перерабатывающей и других отраслях промышленности. Все неньютоновские жидкости можно разделить на три группы: 1. Неньютоновские вязкие жидкости. 2. Неньютоновские нереостабильные жидкости. 3. Неньютоновские вязкоупругие жидкости. Неньютоновские вязкие жидкости характеризуются тем, что их свойства не зависят от времени, а касательное напряжение является простой функцией градиента скорости. Они подразделяются на:
· вязкопластичные жидкости; · псевдопластичные жидкости; · дилатантные жидкости; · нелинейно-вязкопластичные жидкости.
Если к вязкопластичной жидкости прикладывать напряжение сдвига, меньшим по величине, чем τ0, то такая жидкость будет оставаться в покое. Как только напряжение сдвига превысит τ0 вязкопластик начнет течь, как обычная ньютоновская жидкость. Иначе говоря, привести в движение вязкопластичную жидкость можно, лишь преодолев её статическое (предельное) напряжение — это полностью соответствует уже рассмотренной нами реологической модели Бингама. Такое поведение вязкопластиков объясняется тем, что в жидкости, находящейся в покое, образуется жесткая пространственная структура, оказывающая сопротивление любому напряжению, меньшему τ0. При напряжениях, больших τ0, структура полностью разрушается и не препятствует движению жидкости. При напряжениях, меньших τ0, структура вновь восстанавливается, а жидкость перестает течь. К вязкопластичным жидкостям можно отнести буровые растворы, сточные грязи, масляные краски, зубную пасту и т. д. Для неньютоновских вязких жидкостей используется понятие кажущейся или эффективной вязкости. Использование эффективной вязкости позволяет приближенно рассчитывать движение аномальных сред по уравнениям и формулам, полученным для ньютоновских жидкостей. Теоретическая часть
Расчетная часть
|
||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.248.119 (0.055 с.) |
 Ньютоновскими называются жидкости, течение которых подчиняется уравнению Ньютона-Петрова:
Ньютоновскими называются жидкости, течение которых подчиняется уравнению Ньютона-Петрова: — градиент скорости, показывающий изменение скорости течения жидкости du при переходе от слоя к слою, dn — расстояние между слоями жидкости; τ — касательное напряжение (напряжение трения); F — сила внутреннего трения; S — площадь поверхности соприкасающихся слоев жидкости; η — динамический коэффициент вязкости, или ньютоновская вязкость.
— градиент скорости, показывающий изменение скорости течения жидкости du при переходе от слоя к слою, dn — расстояние между слоями жидкости; τ — касательное напряжение (напряжение трения); F — сила внутреннего трения; S — площадь поверхности соприкасающихся слоев жидкости; η — динамический коэффициент вязкости, или ньютоновская вязкость. Рис.1. Кривые течения жидкостей:
Рис.1. Кривые течения жидкостей: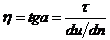
 Кривая течения вязкопластичных жидкостей (рис. 1, линия 2) представляет собой прямую линию, пересекающую ось напряжений τ на расстоянии τ0 её начала. Течение таких жидкостей может быть описано уравнением Шведова-Бингама:
Кривая течения вязкопластичных жидкостей (рис. 1, линия 2) представляет собой прямую линию, пересекающую ось напряжений τ на расстоянии τ0 её начала. Течение таких жидкостей может быть описано уравнением Шведова-Бингама: где τ0 — статическое (предельное) напряжение; η — пластическая вязкость, численно равная тангенсу угла наклона кривой течения:
где τ0 — статическое (предельное) напряжение; η — пластическая вязкость, численно равная тангенсу угла наклона кривой течения: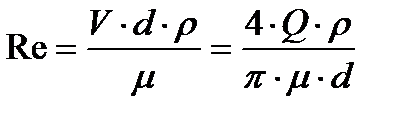 – Формула для нахождения числа Рейнольдса, где V – скорость,
– Формула для нахождения числа Рейнольдса, где V – скорость, – плотность раствора,
– плотность раствора,  – динамический коэффициент вязкости, Q – расход.
– динамический коэффициент вязкости, Q – расход.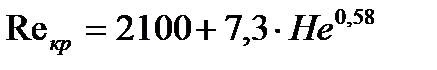 – Формула для нахождения критического числа Рейнольдса, также может быть найдено по кривой (Приложение 2).
– Формула для нахождения критического числа Рейнольдса, также может быть найдено по кривой (Приложение 2). – Формула для нахождения числа Хендстрена, где
– Формула для нахождения числа Хендстрена, где  – динамическое напряжение сдвига.
– динамическое напряжение сдвига. – Формула для нахождения числа Сен – Венана.
– Формула для нахождения числа Сен – Венана. – Формула для перепада давления в кольцевом пространстве при ламинарном режиме течения, где
– Формула для перепада давления в кольцевом пространстве при ламинарном режиме течения, где  – длина участка,
– длина участка,  – коэффициент.
– коэффициент. – Формула для вычисления коэффициента Сен–Венана – Ильюшина, также может быть найден по графику (Приложение 1).
– Формула для вычисления коэффициента Сен–Венана – Ильюшина, также может быть найден по графику (Приложение 1). – Формула Дарси – Вейсбаха для определения перепада давления в трубах, при турбулентном режиме течения.
– Формула Дарси – Вейсбаха для определения перепада давления в трубах, при турбулентном режиме течения. – Формула для определения коэффициента гидравлического сопротивления в трубах.
– Формула для определения коэффициента гидравлического сопротивления в трубах.
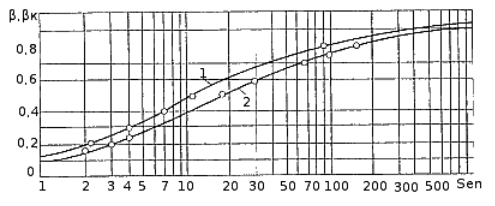 Приложение 1
Приложение 1 Приложение 2
Приложение 2


