
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування ройових алгоритмів до розв’язуванняСодержание книги
Поиск на нашем сайте Задач оптимізації Ройові алгоритми, як вже було сказано, призначені для розв’язку задач оптимізації, або задач пошуку екстремуму(мінімального чи максимального значення). Одними з таких задач є задачі міжгалузевого балансу(МГБ). МГБ в економіці – це метод аналізу взаємозв’язків між різними галузями (секторами) економічної системи. При виробництві продукції (товарів, виконанні робіт та надання послуг) в кожній галузі споживається продукція, що виробляється у своїй та всіх інших галузях економіки. Це означає, що кожна галузь виступає в системі міжгалузевих відношень одночасно як виробник, так і як споживач. Мета міжгалузевого балансу – визначити, скільки продукції повинна виробити кожна галузь для того, щоб задовольнити всі потреби економічної системи в її продукції, тобто задовольнити як внутрішні потреби всіх галузей, так і потреби зовнішнього середовища (кінцевий попит: задоволення особистих потреб людей, суспільних потреб, накопичення продукції, експорт продукції). Сутність принципу балансу – все, що випускається (вал), дорівнює сумі витрат продукції на внутрішні потреби галузей економіки і випуск продукції для зовнішніх потреб (експорт): ВАЛ=ВИТРАТИ (ВНУТРІШНІ ПОТРЕБИ)+ВИПУСК (ЕКСПОРТ). Задача оптимізаційної ж задачі МГБ полягає у тому, щоб знайти вектор валової продукції X *, при якому досягається максимальний прибуток від накопиченої продукції Y* при відомій виробничій потужності галузей Математична модель МГБ Нехай в нас є n галузей, що виробляють продукцію, тоді A={ai,j} – матриця, що показує частку продукції, яка виробляється i-ю галуззю, що споживається j-ю галуззю i,j∈[1;n], X=(x1,x2,…,xn)T – вектор валової продукції, що показує загальну кількість виробленої продукції j-ї галузі, Y=(y1,y2,…,yn)T – вектор, що визначає замовлення на випуск готової продукції i-ю галуззю, що йде на експорт. Класична балансова задача ставить за мету визначити валовий випуск продукції всіх галузей (вектор Х), необхідний для: 1) задоволення внутрішніх потреб, що визначаються діючою технологією і, відповідно, матрицею А; 2) забезпечення замовлення на готову продукцію (вектор Y). Витрати на внутрішні потреби обчислюються як добуток матриці А на шуканий вектор Х:
випуск готової продукції визначається заданим вектором Y, тоді балансова модель визначається системою лінійних рівнянь: в матричному вигляді
або у розгорнутому вигляді
Таким чином, отримуємо, що X=(E-A)-1Y, де E – одинична матриця (n на n), усі елементи якої, крім головної діагоналі, нулі, а на головній діагоналі одиниці.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.20.78 (0.011 с.) |


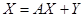 , (1.1)
, (1.1)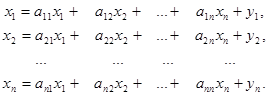 (1.2)
(1.2)


