Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция №1. Тема: теория множества.Стр 1 из 6Следующая ⇒
Лекция №1. Тема: теория множества. Множество – это совокупность каких-либо элементов чего-либо, объединенных неким признаком, общим свойством, присущим всем элементам. Например: человечество, класс, группа и т.д. Множество можно задать словесно, перечислением. Множество считается заданным, если: · Перечислены все его элементы · Либо указано свойства, которым обладают те и только те элементы, которые принадлежат данному множеству.
Примеры записи множества: · Перечисление M = {m1, m2 … mn} N = 1, 2, 3,4 … 10. · Описание множества M = {x│P(x)} – состоит из тех элементов х, которое обладает признаком Р. Свойство Р – характеристическое. · M = {n│n? N, n<5} – M состоит из натуральных чисел, меньше 5.
Если множество не содержит никаких элементов, обладающих характеристическим признаком, то оно называется пустым. Обозначается: Ø. Пример: 1. Множество целых решений 5<x<6 – является пустым
множество признак
2. Множество действительных решений уравнения пустое: x2 + 4 = 0; к = Ǿ; x2 = -4. Действительного решения нет, т.е. это множество – пустое.
Множество конечно, если количество элементов в нем ограничено (бесконечное множество бывает счетное и несчетное). Множество будет счетным, если его элементы можно пронумеровать (считать). Элементы несчетного множества пронумеровать нельзя. Из множества М можно выделить его часть (выделением нового характеристического свойства или перечислением выбранных элементов) – множества К, все элементы которого обладают таким же признаком, что и элементы множества М.
Пример: группу людей разбили на части и получили подмножества.
Множество К называется подмножеством множества М(КЄM), если для любых значений х Є К выполняется условие: х Є M.
Пример: NЄZЄQЄRЄC N – натуральные числа Z – целые числа Q – рациональные числа R – действительные числа C – комплексные (a+ib)
Равными называются два множества, состоящие из одинаковых элементов.
Универсальным называют множество U, состоящее из всех возможных элементов B, обладающих данным признаком, т.е. признаком, общим для всех (понятие универсального множества четко не определено).
Пример: множество букв, слов. Число элементов множества А называется мощностью множества. Обозначается: │А│,U, n (A).
Пример: 1. n(Ø) = 0; 2. M (1, 2, 3): n(M) = 3. Лекции №3. Тема: основные тождества алгебры множеств.
1. 2.
3. 4.
5. 6.
7. 7а.
8. 9. 10. 11.
13. где Ø - пустое множество
Пример: M (1, 9, 12, 17, 33, 4, 16) N (33, 22, 45, 9, 1, 20, 35) 1. вычитание: R = (12, 17, 4, 16); 2. сложение: R = (1, 9, 12, 17, 33, 4, 16, 22, 45, 20, 35); 3. произведение: R = (1, 9, 33)
Лекция №4. Тема: кортежи. Происхождение от французского «торжественность».
Пусть М – конечное множество, элементами которого являются символы. Например: цифры, буквы. Кортеж – есть упорядоченный набор (строгая последовательность) элементов множества M. Алфавит - есть кортеж попарно различных символов, называемых буквами алфавита.
Рассмотрим множество состоящее из n элементов:0,1,2,…,n. Кортежи длины m из этих элементов, обозначим Mm, тогда мощность n(Mm), есть nm. Такие кортежи, которые называются упорядоченными наборами или векторами. Пример: M
Декартовое произведение множеств: Пусть заданы множества M1,M2,…. Mn. Декартовым произведением этих множеств называется множество состоящие из всех кортежей (m1, m2….mn) длины k1(mk Є Mk, M * M *… * M – nраз, обозначается как Mn и называется n – ой степенью M. Порядок задания множителей для декартового произведения, как для кортежей одинаков. Примерами декартовых произведений является таблица умножения, все возможные наборы пар координат на плоскости и т.д.
Пример: M1 = {0, 1, 2}, M2 = {x, y, z}, M3 = {A, Б, С} Декартовое произведение: M1 * M2 * M3
Отображения множеств (функций) Отображение f множества x во множество y – это когда каждому элементу x Є X, ставится в соответствие только один элемент y Є Y.
Элемент y множества Y, соответствующий при отображении f элементу x из X называется образом элемента x. Если y = f(x), то x называется прообразом элемента y при этом отображении. Частный случай отображения множества X в Y имеет место, если каждый элемент множества Y имеет прообраз из множества X. В этом случае отображение (f) сюръективно, (может быть случай, когда несколько элементов Y имеют один и тот же прообраз в X). Отображение f, называется инъективным, если для каждого элемента y Є Y существует не более 1- го прообраза, если отображение f сюръективно и инъективно, то оно называется биективным. Пример: функций, отображающих x Є R на множество y Є R на множество y Є R, где R – множество (бесконечное) действительных чисел.
1. f1(x) = Ex – инъективно (не сюръективно) 2. f2(x) = x*(x2-1) – сюръективно (не инъективно) 3. f3(x) = 3x+1 – биективно
Лекция №5. Тема: алгебра логики (булева алгебра).
В основе логико – математической теории дискретной математики лежит понятие: высказывание. Это повествовательное предложение, которое интересует математика прежде всего в узком смысле: истинно оно или ложно.
В алгебре логики основными связками (операциями) являются следующие: o дизъюнкция (или) o конъюнкция (и) o отрицание (не) o импликация (если…, то…) → o эквиваленция (тогда и только тогда, когда…) ↔ o штрих Шеффера (антиконъюнкция) | o стрелка Пирса (антидизъюнкция) ↓
При выполнении операций существует следующий порядок: - операции в скобках, если их нет тот операции выполняются так: I. отрицание II. конъюнкция III. дизъюнкция IV. импликация V. эквиваленция VI. штрих Шеффера VII. стрелка Пирса Конъюнкцией двух высказываний X, Y называется высказывание (функция) x
Дизъюнкция X и Y называется высказывание (функция) X
Импликацией X и Y называется высказывание (функция) X→Y, которая ложна тогда, и только тогда, когда X истинно, а Y ложно, и истинна в остальных вариантах.
Таблица истинности для импликации
Эквиваленцией X иY называется высказывание X↔Y, которое истинно тогда, и только тогда, когда X и Y оба истинны или ложны, одновременно.
Таблица истинности для эквиваленции
Штрих Шеффера (антиконъюнкция) - X│Y = X∩Y
____ Стрелка Пирса (антиконъюнкция) - X↓Y = XUY
____ Сложение по модулю два (антиэквиваленция) - X
Равносильные формулы.
Дизъюнктивные и конъюнктивные нормальные формы формул алгебры логики (булевой алгебры).
Дизъюнктивной нормальной формой (ДНФ) какой либо формулы алгебры логики называется формула, являющаяся дизъюнкцией элементарных конъюнкций.
Пример:
Формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных сумм (дизъюнктивных одночленов), называется конъюнктивной нормальной формой (КНФ), данной формулы. Например:
ДНФ называется дизъюнкция конечного числа элементарных конъюнкций.
КНФ называется конъюнкция конечного числа элементарных дизъюнкций.
Равносильные формулы:
1) X→Y=
2) X↔Y= (X
3) Закон Де Моргана 4) 5) X↓Y=
Примеры: 1. 2.
Совершенные СДНФ и СКНФ Нормальные формы (ДНФ) (КНФ) называются совершенными (СДНФ, СКНФ), если в каждой элементарной дизъюнкции (конъюнкции) представлены все переменные, входящие в данную формулу, сами, либо с отрицанием.
Существует ДНФ (X
Примеры: СДНФ – CКНФ - Карта Карно Пример: _ 1. F = f(XYZ) = XYZ
_ _ 1) (XYZ _ _ _ _ _ _ 2) (XYZ _ _ _ _ _ _ 3) F = f(XYZ) = XYZ
_ _ _ _ _ _ _ _ _ _ _ _ _ 2. F = ABCD
Если несколько единичек в карте Карно расположены на соседних клетках, то каждая единичка может и должна включаться во все контура, которые могут образоваться. _ _ _ _ _ _ _ _ _ _ 1) (ABCD _ _ _ _ _ _ 2) (ABCD _ _ _ _ _ _ _ _ _ _ 3) (ABCD _ _ _ _ _ _ 4) f(ABCD) = ABD _ _ _ 5) f(ABCD) = AD
_ _ _ _ _ _ _ _ 3. F = x1x2x3x4 _____ ___ ___ _ _ _ _ _ 1) (x1x2x3x4 __ __ _ _ _ 2) (x1x2x3x4 _ _ _ _ __ _ 3) F = (x2x3x4
Теорема Поста. Операции по модулю два, основные законы:
1) x1 2) (x1 3) для конъюнкции: x1*(x2 4) операции с конъюнкцией: _ _ x _____ _ _ 5) x1 _ _ 6) x1
Теорема: Любую булеву функцию можно представить в виде многочлена Жегалкина, который есть сумма констант и различных одночленов (конъюнкций), в которые каждые из переменных входят не выше чем в первой степени.
Любая функция булевой алгебры может быть представлена, и притом единственным образом, с помощью многочлена Жегалкина вида: n F = i, j = 0
Многочлен Жегалкина булевой функции одной переменной: 1) F(A) = a1 2) F(X) = a0 3) F(Я) = a0 4) Многочлен Жегалкина булевой функции двух переменных: 1) F(A, B) = a0 2) F(x1, x2) = a0
Многочлен Жегалкина булевой функции трёх переменных: 1) F(x1, x2, x3) = a0
_ _ _ _ _ _ _ _ _ _ _ F = (x1 _ _ _ _ _ _ = 1
Теорема Поста.
Для того, чтобы система булевых функций {f1, f2,… fn} была полной, необходимо и достаточно, чтобы для каждого из классов Т0, Т1, S L M начиналась функция fi не принадлежащая этому классу. Т0 - класс функций сохраняющих 0; Т1 - класс функций сохраняющих 1; S - класс самодвойственных функций; L - класс линейных функций; M – класс монотонных функций.
Множество булевых функций называется функционально-замкнутым, если вместе с функциями из данного класса оно содержит также все их суперпозиции. Система булевых функций {f1, f2,… fn} называется полной, если любая из этих функций (fi) может быть выражено через другие функции с помощью суперпозиции, например:
f3 = f1 + f2 f1 + f2 - f4 f1 = f3+f5+f6 - f7 - f8
(f1, f1, … fn; f1 + f2; f1 + f3)
Примеры важнейших замкнутых классов: Т0 : f(0, 0, 0) = (0 Т1: f(1, 1, 1) = 1 Лекция №12. Тема: Кванторы.
1. Квантор общности Ұ х (Z(x)) – для любого х существует Z(x). 2. Квантор существования Например, «для каждого х существует y, равный х2» записывается так: Ұх Переменная, к которым относиться квантор называется связанным. Примеры применения кванторов: 1) х*х = х2 2) х+2 = 7
Пусть A и B формулы алгебры логики, причем нет таких переменных, которые были бы связанны в одной формуле и свободны в другой, тогда: A = x1 (A
Правила переходов от одних формул к другим: o перенос квантора через отрицание. Пусть А – формула, где х – свободная переменная, тогда _ _ _ Ұх (А(х)) ≡ _ _
Перенос квантора через отрицание. ________ ___ (Ұх)(Ұ(х)) ≡ ( ____
Вынос квантора за скобки: ( ( (Vх)(V(х) (Vх)(V(х)
Исчисление предикатов. В исчислении предикатов указывается некоторая совокупность формул, которые называются аксиомами и составляют аксиоматическую теорию, а также указывается конечное множество отношений между формулами, составляются правила вывода.
Аксиомы исчисления: 1) А → (B → А) 2) (А→ (B → C)) → ((А → B) → (A → C) _ _ _ 3) (B → А) → ((B → А) → (A → C)) 4) (V x1)A(хi) → A(хj), где A(хi) не содержит xj 5) A(хi) → (
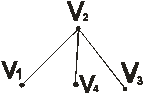
Примеры графов
1) 3)
4)
Пусть на плоскости задано некоторое множество вершин V и дуг R. Графом называют бинарное отношение множеством V и R или иначе f V → R. Здесь f отображение инциденции.
Граф называется ориентированным, если указано направление дуг и неориентированным, если такое направление не указано. Граф называется петлёй, если его начало и конец совпадают. Под графом Ga графа G называется граф, который входит в лишь часть вершин графа G вместе с дугами их соединяющими. Частным графом Gв графа G называется граф, который входит в лишь часть дуг графа G вместе с вершинами их соединяющими. (Карта шоссейных дорог – это граф. Дороги Саратовской области – это подграф, а главные дороги – это частный граф, где вершины называются смежными, если существует соединяющая их дуга. Два смежных ребра имеют общую вершину). Степенью (валентностью) вершины называется число инцидентных ей рёбер. Кратностью пары вершин называется число соединяющих их ребер или дуг. Граф, состоящий из изолированных вершин, называется нульграф. Теорема В графе G(V, R) сумма степеней всех его вершин – число четное равное удвоенному n числу ребер графа: i= 1 m =│R│ - число ребер графа
Вершина называется четной/нечетной, если её степень – четная/нечетная. Ориентированные графы изображаются так: V2 V2 V1
Неориентированный граф – ребро, цепь, цикл; Ориентированный граф – дуга, путь, контур.
Ребро (дуга) – отрезок, соединяющий две вершины. Цель (путь) – последовательность ребер (дуг). Цикло (контур) – конечной длины цель (путь), у которой начальная и конечная вершины совпадают.
Граф называется связанным, если любые две его вершины можно соединить цепью. Граф сильно связан, если для любых двух вершин хi ≠ хj существует путь, идущий из хi и хj. Граф, который не является связанным, может быть разбит на конечное число связанных графов, называемых компонентами связанности.
V3 V3
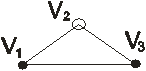
V1 V5 графа G У графа может быть несколько подграфов. Граф G называется полным, если любые две его различные вершины напрямую соединены как минимум одним и ребром. V3
V1 V5 _ Дополнением графа G(V, R) называется граф G(V, R) с теми же вершинами V, что и граф G и имеющие те и только те ребра R, которые необходимо добавить в графу G, чтоб он стал полным. Граф с кратными ребрами не имеет дополнения.
- граф _ G(V,R) - V1 V4 Маршрут – это последовательность ребер неориентированного графа, когда вершина предыдущего ребра совпадает с следующего ребра. Число ребер маршрута называется его длиной. В маршруте одно и тоже ребро может встретиться несколько раз; если ребра встречаются один раз, то маршрут называется цепью. В ориентированном графе маршрут называется путь – упорядоченная последовательность дуг ориентированного графа, соединенных последовательно. § Направление каждой дуги должно совпадать с направлением пути. Путь навстречу дуги невозможен. § Не одна дуга пути не должна встречаться дважды.
Лекция №1. Тема: теория множества. Множество – это совокупность каких-либо элементов чего-либо, объединенных неким признаком, общим свойством, присущим всем элементам. Например: человечество, класс, группа и т.д. Множество можно задать словесно, перечислением. Множество считается заданным, если: · Перечислены все его элементы · Либо указано свойства, которым обладают те и только те элементы, которые принадлежат данному множеству.
Примеры записи множества: · Перечисление M = {m1, m2 … mn} N = 1, 2, 3,4 … 10. · Описание множества M = {x│P(x)} – состоит из тех элементов х, которое обладает признаком Р. Свойство Р – характеристическое. · M = {n│n? N, n<5} – M состоит из натуральных чисел, меньше 5.
Если множество не содержит никаких элементов, обладающих характеристическим признаком, то оно называется пустым. Обозначается: Ø. Пример: 1. Множество целых решений 5<x<6 – является пустым
множество признак
2. Множество действительных решений уравнения пустое: x2 + 4 = 0; к = Ǿ; x2 = -4. Действительного решения нет, т.е. это множество – пустое.
Множество конечно, если количество элементов в нем ограничено (бесконечное множество бывает счетное и несчетное). Множество будет счетным, если его элементы можно пронумеровать (считать). Элементы несчетного множества пронумеровать нельзя.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.53.68 (0.31 с.) |

 M = {x│x Є N, 5<x<6} = Ø
M = {x│x Є N, 5<x<6} = Ø
 Пример:
Пример:
 M1 (1, 2, 3) а) б)
M1 (1, 2, 3) а) б) M 2 (1, 3, 2)
M 2 (1, 3, 2) M 3 (3, 2, 1)
M 3 (3, 2, 1)

 Коммутативность
Коммутативность

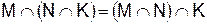 Ассоциативность
Ассоциативность

 Дистрибутивность
Дистрибутивность Закон
Закон Де Моргана
Де Моргана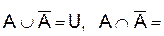 Ø
Ø  Ø
Ø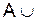 Ø
Ø 

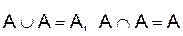
 Ø = Ø
Ø = Ø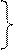 12.
12.  Закон
Закон поглощения
поглощения (1,2,3,4), M
(1,2,3,4), M  (4,3,2,1) M
(4,3,2,1) M  (1,3,2,4); M
(1,3,2,4); M  1 ≤ k ≤ n), где m1Є M1, m2 Є M2, … mn Є Mn. Обозначается как M1*M2*…Mn. Произведение –
1 ≤ k ≤ n), где m1Є M1, m2 Є M2, … mn Є Mn. Обозначается как M1*M2*…Mn. Произведение – K1 = {(0, 1), (x, y), (A, Б)}, или К2 = {(1, 2), (x, z), (A, C)}.
K1 = {(0, 1), (x, y), (A, Б)}, или К2 = {(1, 2), (x, z), (A, C)}.




 Y = X↔Y
Y = X↔Y
 – КНФ
– КНФ - ДНФ
- ДНФ - КНФ
- КНФ (X
(X  )
) )
) ;
; 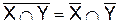

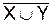





 XYZ X
XYZ X 






 x2 = x2
x2 = x2  x1 * x2
x1 * x2 aixixj
aixixj (x1
(x1 
 - «существует»:
- «существует»:  Ұ (х)(х*х = х2) = истинно (1)
Ұ (х)(х*х = х2) = истинно (1) x2
x2 

 2)
2)
 5) 6)
5) 6)
 V3 V1
V3 V1  V3
V3 - G(V, R) – граф V2
- G(V, R) – граф V2  V4 - Gа(V, R) – подграф
V4 - Gа(V, R) – подграф