
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез передаточного шарнирного четырехзвенникаСодержание книги
Поиск на нашем сайте Порядок разработки практической части курсовой работы рассматривается на нескольких примерах. В качестве первого примера выбрана задача проектирования шарнирного четырехзвенника. Ниже приведено условие задачи, которое студент должен поместить при составлении пояснительной записки в подраздел «Полная постановка задачи» раздела «Алгоритмический анализ задачи».
2.1 Полная постановка задачи Спроектировать шарнирный плоский кривошипно-коромысловый четырехзвенник, ведущее звено которого – кривошип АВ – совершает равномерное вращательное движение во времени (рисунок 2.1).
Рисунок 2.1 - Шарнирный четырехзвенник Коромысло СD движется по закону: y = K sin(j + j0). Проверить, соответствуют ли вычисленные значения параметров a (длина кривошипа), b (длина шатуна) и c (длина коромысла) с заданными значениями a и b условиям существования механизма и ограничениям: u £ uд a < d Рассчитать значение функции погрешности YD(j), построить графики зависимости Y(f) и Y(f)+YD(j). В общем случае при синтезе плоского шарнирного четырехзвенника требуется подобрать пять параметров: относительные длины звеньев a, b, c (d=1) и начальные углы a и b таким образом, чтобы проектируемый механизм обеспечивал определенный закон преобразования движения Y=f(j), 0£j£jm, и максимальный угол давления шатуна на звено CD был меньше допустимого значения uд[2]. В основу методики решения сформулированной задачи положен метод синтеза механизмов на основе приближающих функций, разработанный П.Л. Чебышевым и получивший развитие в работах Н.И. Левитского [3]. По этой методике углы a и b задаются в качестве исходных данных, а параметры механизма вычисляются по формулам:
где параметры pj (j=0,1,2) есть неизвестные в системе линейных уравнений вида:
В этой системе коэффициенты
Для определения ¡ используют равенство
В (2.3) и (2.4) функции fk (j) (k = 0,1,2) и F(j) задаются в виде: f0 (j) = cos(a+j) f1 (j) = cos(b+y) f2 (j) = 1 F(j) = cos(a+j - b - y) (2.5) где, в соответствии с заданием y = K sin(j + j0). Угол давления определяется по формуле: u = arcsin [(b2 + c2 – l2)] / 2 * b * c, где l2 = a2 + 1 – 2a * c * cos(j). (2.6) Полученный угол давления при j = 0 является максимальным и должен удовлетворять условиям u £ uд (2.7) Для определения погрешности воспользуемся формулой: DY = DQ / (2bc cos(u), где DQ = - 2ac [ p0f0(j) + p1f1(j) + p2f2(j) – F(j)] (2.8)
Проработав условие задачи, студент должен приступить к выполнению алгоритмического анализа задачи, последовательность проведения которого ему известна из курса «Информатика».
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |



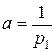 ,
,  ,
,  (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4)


