
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конфликтной задачи ОптимизацииСодержание книги
Поиск на нашем сайте
Пример постановки задачи на составление оптимального производственного плана в условиях чистого риска
Предприятие ежедневно выпускает два вида скоропортящейся продукции. Сбыт зависит от погодных условий. На реализацию всей произведенной за день продукции расходуется 200 у.е.
Если продукция не реализуется в день выпуска, то ее качества значительно снижаются, и она гарантированно продается после завершения торговли по цене в 4 раза меньше отпускной. Требуется: а) составить ежедневный план производства, при котором прибыль максимальна, а риск минимален; б) составить ежедневный план производства, при котором прибыль максимальна, а допустимый риск равен 0,3.
Предварительный этап решения. Для предприятия ежедневный сбыт продукции не гарантирован, т.е. из-за неопределенности погоды возникает чистый риск. Эту ситуацию можно считать конфликтной (игровой). Построим модель для определения оптимального плана в виде матричной игры двух лиц.
Можно, конечно, не считать, что природа разумный противник, и она не будет изучать поведение предприятия с целью максимально навредить ему, и поэтому не следует считать такую ситуацию антагонистической игрой. Тогда можно изучить статистические данные о поведении погоды, и строить план производства с учетом состояния погоды в среднем (применить статистические методы принятия решений). Однако игровой подход имеет свои преимущества. Рассматривая природу как противника, предприятие может строить план производства с учетом наиболее неблагоприятных действий природы, а если природные условия будут благоприятными для предприятия, то этот оптимальный план поведения предприятия даст возможность ему увеличить свою прибыль. Составим матрицу выигрышей (в Вашем варианте задания эта матрица задана) Составим матрицу производственных планов (в Вашем варианте задания эта матрица задана) Так как данная игровая ситуация повторяется многократно, то для игроков имеют смысл не только чистые, но и смешанные стратегии – вероятности (частоты) применения игроками чистых стратегий (базовых планов – предприятием, погодных условий – природой. Предположим, что на рассматриваемую перспективу по прогнозу погоды известны вероятности наступления хорошей (0,75) и плохой погоды (0,25). Тогда для второго игрока ориентировочно известна оценка его смешанной стратегии Часто смешанная стратегия оценивается в результате обработки экспертных оценок с помощью метода Саати. При выполнении индивидуального задания выберите оценку смешанной стратегии игрока 2 (как вектор приоритетов!) и риск (от 0 до 1) произвольно самостоятельно. Итак, задача планирования сведена к игровой задаче об отыскании оптимальных стратегий (чистых, смешанных и скорректированных) игроков.
К началу ↑ Предварительный этап решения задачи в программе Excel
На предварительном этапе требуется определить: 1) нижнюю и верхнюю цены игры; 2) наличие седловой точки (их м.б. и несколько); 3) выделить чистые стратегии, оптимальные по Парето. Если игра имеет седловую точку, то она может быть решена в чистых стратегиях. Тогда уже на предварительном этапе требуется определить и указать на листе Excel: 1) оптимальные чистые стратегии игроков; 2) оптимальную цену игры. (Далее, при решении игры в смешанных стратегиях, оказывается, что вектор оптимальной смешанной стратегии содержит компоненты 0 с номерами, соответствующими неоптимальным чистым стратегиям, т.е. их вероятности применения равны 0 – они не применяются никогда.) Пример. Допустим, задана игра с матрицей выигрышей
Здесь:
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.203.35 (0.006 с.) |

 (на примере работы с программами Excel, Mathcad)
(на примере работы с программами Excel, Mathcad) =
= 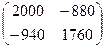 , элемент a ij (i =1,2; j =1,2) в матрице A - прибыль предприятия за день (один ход игры), если предприятие применяет свою i -ю стратегию, а природа свою j -ю стратегию.
, элемент a ij (i =1,2; j =1,2) в матрице A - прибыль предприятия за день (один ход игры), если предприятие применяет свою i -ю стратегию, а природа свою j -ю стратегию. =
=  , элемент w ij (i =1,2; j =1,2) в матрице W – объем производства продукта Пj при плане № i. (предприятия предприятие применяет свою i -ю стратегию).
, элемент w ij (i =1,2; j =1,2) в матрице W – объем производства продукта Пj при плане № i. (предприятия предприятие применяет свою i -ю стратегию). . (Причем это, вообще говоря, не оптимальная стратегия второго игрока!) Кроме того, известна оценка чистого риска R=0,3 (вероятность реализации прогноза погоды). С точки зрения использования в расчетах – это допустимый для игрока 1 уровень риска.
. (Причем это, вообще говоря, не оптимальная стратегия второго игрока!) Кроме того, известна оценка чистого риска R=0,3 (вероятность реализации прогноза погоды). С точки зрения использования в расчетах – это допустимый для игрока 1 уровень риска.



