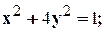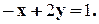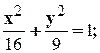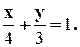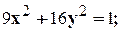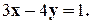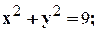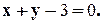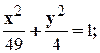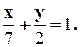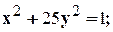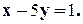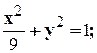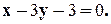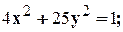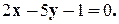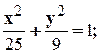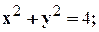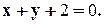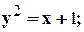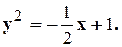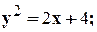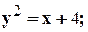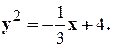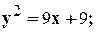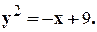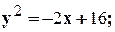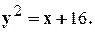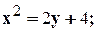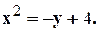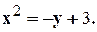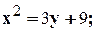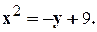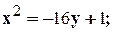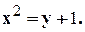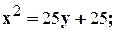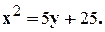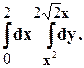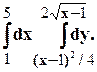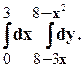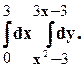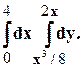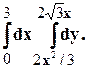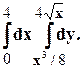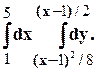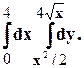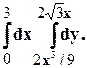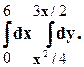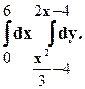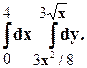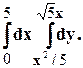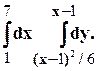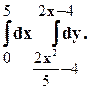Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения, их порядок, общий и частные интегралы
Введение
Целью настоящих методических указаний является помощь студентам – заочникам в выполнении контрольной работы №3. Перед выполнением контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы и воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях. Номер варианта по каждому заданию студент выбирает по формуле где
Пример. Пусть шифр студента 1235, тогда: номер варианта первого задания: номер варианта второго задания: номер варианта третьего задания: номер варианта четвертого задания: Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом. Если итоговая число по формуле получится больше 20, то для опред еле ния варианта от полученного числа отнимают 20.
Пример. Пусть шифр студента 1298. Номер варианта второго задания: Основная цель инженера – исследователя, изучающего какой- либо физический или технический процесс, заключается в выявлении его закономерностей, в получении аналитического выражения функциональной зависимости между переменными параметрами этого процесса. Большинство подобных задач сводится к решению уравнений, содержащих производные или дифференциалы неизвестных функций.
Знакоположительные ряды
Для числовых рядов с положительными членами Интегральный признак Коши Ряд с положительными убывающими членами Нижним пределом несобственного интеграла может быть любое число Пример 7. Исследовать сходимость гармонического ряда: Решение: Заменяем в выражении общего члена
Признак Даламбера Если Пример 8. Исследовать на сходимость ряд Решение:
Применим признак Даламбера:
Признак сравнения Пусть даны два ряда с положительными членами
если начиная с некоторого номера n: 1) 2) При использовании этого признака исследуемый ряд часто сравнивается либо с бесконечной геометрической прогрессией
Пример 9 Исследовать ряд на сходимость с помощью признака сравнения Решение: Каждый член
Знакопеременные ряды Если знаки членов ряда (1) строго чередуются, то ряд называется знакочередующимся (знакопеременным). Знакопеременный ряд
Знакопеременный сходящийся ряд (2) называется условно сходящимся, если ряд (3) расходится. Всякий абсолютно сходящийся ряд есть ряд сходящийся.ъ
Признак Лейбница Знакочередующийся ряд Пример 10. Доказать сходимость ряда Решение:
Функциональные ряды Ряд При различных значениях Совокупность значений Из всех функциональных рядов простейшими и наиболее употребительными являются степенные ряды вида
или Областью сходимости всякого степенного ряда является интервал числовой оси, симметричный относительно точки Для определения области сходимости обычно вначале используется признак Даламбера, а затем те значения Пример 11. Найти область сходимости ряда Решение:
И определяем, при каких х этот ряд будет сходиться:
При При Ряды Тейлора Рядом Тейлора для функции При а =0 ряд Тейлора есть степенной ряд относительно независимой переменной х: который принято называть рядом Маклорена. Разложение в ряд Маклорена некоторых функций
Применение рядов к приближенным вычислениям Для вычисления приближенных значений функций с заданной точностью удобно пользоваться рядами в том случае, когда соответствующий ряд является знакочередующимся; для знакочередующегося ряда легко оценить погрешность приближенного значения суммы - она меньше абсолютного значения первого из отброшенных членов. Пример 12. Вычислить Решение:
Разложим подынтегральную функцию Заменив в разложении функции
Следовательно,
=
Варианты индивидуальных заданий Задание 1. Найти общий интеграл уравнения . 1. 2.
3. 4. 5. 6. 7. 8. 9. 10.
11.
12. 13. 14. 15. 16. 17.
18. 19.
20.
Задание 2. Найти частное решение (частный интеграл) уравнения. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. Задание 3. Найти общее решение дифференциального уравнения. 1.
2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20.
Задание 4. Найти общее решение дифференциального уравнения. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
Задание 5. Написать три первые члены ряда. Найти интервал сходимости и исследовать ряд на сходимость на концах интервала.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. Задание 6. Вычислить определенный интеграл с точностью до 0,001 путем разложения подынтегральной функции в ряд и почленного интегрирования этого ряда. 1. 3. 5. 7. 9. 11. 13. 15. 17. 19.
Двойные интегралы 5.1 Основные понятия и определения Пусть в замкнутой области В каждой области
Эта сумма называется функции Если существует предел интегральной суммы, не зависящий от способа разбиения области
Таким образом,двойной интеграл определяется равенством
В этом случае функция Случайные величины
Случайной величиной называют переменную величину, которая в результате испытания случайно принимает одно из множества возможных значений. Случайную величину, возможные значения которой можно записать в виде конечной или бесконечной последовательности, называют дискретной случайной величиной. Случайную величину, которая может принимать все значения из некоторого числового промежутка называют непрерывной случайной величиной.
Варианты заданий
Задание 7. Данную функцию z= f (x, y) исследовать на экстремум.
1. z= 2. z= 3. z= 4. z= 5. z= 6. z= 7. z= 8. z= 9. z= 10. z= 11. z= 12. z= 13. z= 14. z= 15. z= 16. z=
17. z= 18. z=
19. z= 20. z=
1. z= 2. z= 3. z= 4. z= 5. z= 6. z= 7. z= 8. z=
9. z= 10. z=
Вычислить частные производные первого и второго порядков от заданных функций.
11. z= 12. z= 13. z= 14. z= 15. z= 16. z=
17. z= 18. z= 19. z= 20. z=
Задание 9. С помощью двойного интеграла вычислить координаты центра тяжести фигуры, ограниченной заданными линиями (поверхностную плотность считать равной единице).
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
13. 14. 15. 16.
17. 18. 19. 20.
Задание 10. Требуется: 1) построить на плоскости хОу область интегрирования заданного интеграла; 2) изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядках интегрирования. 1. 2. 3.
4. 5. 6. 7. 8. 9.
10. 11. 12. 13. 14. 15.
16.
17. 18. 19. 20.
Задание 11. Заданы математическое ожидание m и среднее квадратическое отклонение s нормально распределенной случайной величины х. Найти: 1) вероятность того, что х примет значение, принадлежащее интервалу (a, b); 2) вероятность того, абсолютная величина отклонения |x-m| окажется меньше d.
1. m=15, s=2, a=16, b=25, d=4. 2. m=14, s=4, a=18, b=34, d=8. 3. m=13, s=4, a=15, b=17, d=6. 4. m=12, s=5, a=17, b=22, d=15. 5. m=11, s=3, a=17, b=26, d=12. 6. m=10, s=2, a=11, b=13, d=5. 7. m=9, s=4, a=15, b=19, d=18. 8. m=8, s=2, a=6, b=15, d=8. 9. m=7, s=5, a=2, b=22, d=20. 10. m=6, s=3, a=0, b=9, d=9. 11. m=15, s=2, a=9, b=19, d=3. 12. m=14, s=4, a=10, b=20, d=4. 13. m=13, s=4, a=11, b=21, d=8. 14. m=12, s=5, a=12, b=22, d=10. 15. m=11, s=4, a=13, b=23, d=6. 16. m=10, s=8, a=14, b=18, d=2. 17. m=9, s=3, a=9, b=18, d=6. 18. m=8, s=4, a=8, b=12, d=8. 19. m=7, s=2, a=6, b=10, d=4. 20. m=6, s=2, a=4, b=12, d=4.
Задание 12 1. В цехе работают 6 мужчин и 4 женщины. По табельным номерам на удачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины. 2. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников. 3. Собрание, на котором присутствуют 25 человек, в том числе 5 женщин, выбирает делегацию из 3 человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти вероятность того, что в делегацию войдут 2 женщины и 1 мужчина. 4. Вероятность попадания в мишень при одном выстреле для первого стрелка равна р, а для второго – 0.7. Известно, что вероятность ровно одного попадания при одном выстреле обоих стрелков равна 0.38. Найдите р. 5. Бросают 4 игральные кости. Найти вероятность того, что на всех выпадет одинаковое число очков. 6. В партии из 10 изделий имеется 4 бракованных. Наугад выбирают 5 изделий. Определить вероятность того, что среди этих 5 изделий окажется 3 бракованных. 7. Три стрелка стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0.75; для второго – 0.8, для третьего – 0.9. Найти вероятность того, что: 1) все три стрелка попадут в цель; 2) все трое промахнутся; 3) только один стрелок попадет в цель; 4) хотя бы один стрелок попадет в цель.
8. В первом ящике 6 белых и 4 черных шара, во втором – 7 белых и 3 черных. Из каждого ящика наугад вынимают по одному шару. Чему равна вероятность того, что вынутые шары разного цвета? 9. На двух станках производятся одинаковые детали. Вероятность того, что деталь стандартная, для первого станка равна 0.8, для второго – 0.9. Производительность второго станка втрое больше, чем первого. Найти вероятность того, что взятая наудачу деталь окажется стандартной. 10. Из партии, в которой 20 деталей без дефектов и 5 с дефектами, берут наудачу 3 детали. Чему равна вероятность того, что: 1) все три детали без дефектов; 2) по крайней мере одна деталь без дефектов? 11. Слово «карета», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают буквы одну за другой. Какова вероятность получить при таком извлечении слова «ракета»? 12. Ящик содержит 10 деталей, среди которых 3 стандартных. Найти вероятность того, что из наудачу отобранных 5 деталей окажется не более одной стандартной. 13. Брошены два одинаковых игральных кубика. Найти вероятность того, что цифра 6 появиться хотя бы на одной грани. 14. Для поражения цели достаточно попадания хотя бы одного снаряда. Произведено два залпа из орудий. Найти вероятность поражения цели, если вероятность попадания в цель при одном выстреле из первого орудия равна 0.3, а из второго - 0.4. 15. Монету бросают 5 раз. Найти вероятность того, что «герб» выпадет: а) менее 2 раз; б) не менее 2 раз. 16. Найти вероятность того, что событие А произойдет не менее 2 раз в 4 независимых испытаниях, если вероятность наступления события А в одном испытании равна 0.6. 17. Вероятность наступления события А хотя бы один раз при трех испытаниях равна 0.936. Найти вероятность наступления события А при одном испытании. 18. Пусть вероятность того, что телевизор потребует ремонта в течении гарантийного срока, равна 0.2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) не более одного потребует ремонта; б) хотя бы один не потребует ремонта. 19. Вероятность выиграть по лотерейному билету равна 1/7. Найти вероятность выиграть не менее чем по двум билетам из шести. 20. Вероятность попадания при каждом выстреле равна 0.4. Найти вероятность разрушения объекта, если для этого необходимо не менее трех попаданий, а сделано 15 выстрелов.
Задание 13. Две независимые дискретные случайные величины Х и У заданы своими законами распределения. Найти математическое ожидание и дисперсию для случайно величины Z=3X-2Y. 1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.199 (0.01 с.) |
 ,
,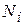 - номер варианта,
- номер варианта,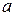 -номер задания,
-номер задания,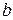 -предпоследняя цифра шифра студента,
-предпоследняя цифра шифра студента,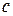 -последняя цифра шифра.
-последняя цифра шифра. =
= 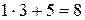 ;
;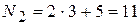 ;
;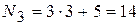 ;
;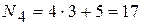 .
.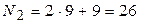 . Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу варианта №6.
. Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу варианта №6.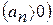 , при исследовании сходимости используются следующие достаточные признаки.
, при исследовании сходимости используются следующие достаточные признаки.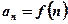 сходится или расходится в зависимости от того, сходится или расходится несобственный интеграл
сходится или расходится в зависимости от того, сходится или расходится несобственный интеграл 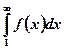 , где
, где 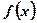 - непрерывная убывающая функция.
- непрерывная убывающая функция.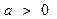 из области определения
из области определения 

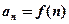 номер n непрерывной переменно
номер n непрерывной переменно  и убеждаемся, что
и убеждаемся, что 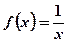 является непрерывной убывающей функции при
является непрерывной убывающей функции при 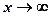 Вычислим несобственный интеграл
Вычислим несобственный интеграл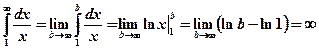 .Несобственный интеграл расходится, следовательно, расходится и гармонический ряд.
.Несобственный интеграл расходится, следовательно, расходится и гармонический ряд.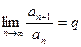 ,то при q <1ряд сходится, а при q >1расходится. При q =1 вопрос о сходимости ряда остается нерешенным.
,то при q <1ряд сходится, а при q >1расходится. При q =1 вопрос о сходимости ряда остается нерешенным.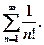
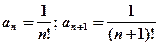 .
.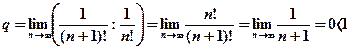 .Так как
.Так как 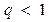 то по признаку Даламбера исследуемый ряд сходится.
то по признаку Даламбера исследуемый ряд сходится.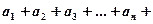 … (а)
… (а)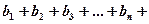 … (б)
… (б)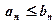 и ряд (б) сходится, то и ряд (а) также сходится;
и ряд (б) сходится, то и ряд (а) также сходится;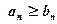 и ряд (б) расходится, то и ряд(а) также расходится.
и ряд (б) расходится, то и ряд(а) также расходится. , которая при
, которая при 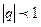 сходится, а при
сходится, а при 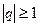 расходится, либо с гармоническим рядом.
расходится, либо с гармоническим рядом.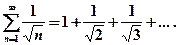
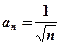 данного ряда, начиная со второго, больше соответствующего члена гармонического ряда:
данного ряда, начиная со второго, больше соответствующего члена гармонического ряда: 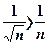 , и, так как гармонический ряд расходится, то, согласно признаку сравнения, исходный ряд также расходится.
, и, так как гармонический ряд расходится, то, согласно признаку сравнения, исходный ряд также расходится.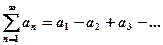 (2) называется абсолютно сходящимся если ряд,
(2) называется абсолютно сходящимся если ряд,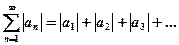 (3), составленный из абсолютных значений его членов сходится.
(3), составленный из абсолютных значений его членов сходится.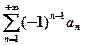 ,
, 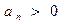 сходится, если его члены убывают по абсолютному значению, стремясь к нулю, т.е. если
сходится, если его члены убывают по абсолютному значению, стремясь к нулю, т.е. если 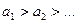 и
и 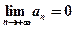 .
.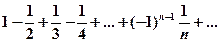
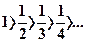 ,
, 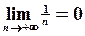 . Условия признака Лейбница выполняются, следовательно ряд сходится.
. Условия признака Лейбница выполняются, следовательно ряд сходится.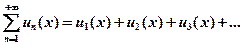 , члены которого являются функциями от переменной
, члены которого являются функциями от переменной 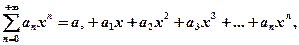 (4)
(4)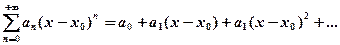 (5)
(5)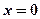 (для ряда (4)) или
(для ряда (4)) или 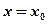 (для ряда (5)), который может быть закрытым, открытым или полуоткрытым.
(для ряда (5)), который может быть закрытым, открытым или полуоткрытым.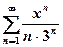 .
.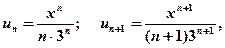 далее по признаку Даламбера ищем
далее по признаку Даламбера ищем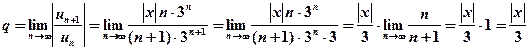
 .
. получаем ряд
получаем ряд  , который сходится по признаку Лейбница (см. пример 10).
, который сходится по признаку Лейбница (см. пример 10).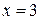 получаем гармонический ряд, который, как известно, расходится. Таким образом, интервалом сходимости данного степенного ряда является полуоткрытый интервал
получаем гармонический ряд, который, как известно, расходится. Таким образом, интервалом сходимости данного степенного ряда является полуоткрытый интервал 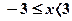 .
.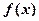 в окрестности точки а называется степенной ряд относительно (х-а):
в окрестности точки а называется степенной ряд относительно (х-а): 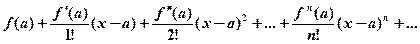
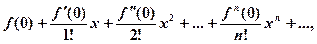
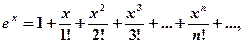
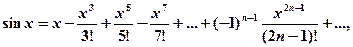
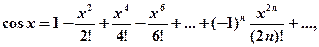
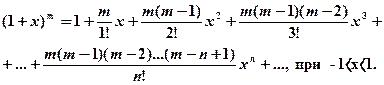
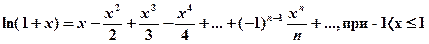
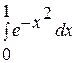 с точностью до 0,001.
с точностью до 0,001. в степенной ряд и затем почленно проинтегрируем полученный сходящийся ряд в указанных пределах.
в степенной ряд и затем почленно проинтегрируем полученный сходящийся ряд в указанных пределах.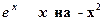 , получим искомое разложение:
, получим искомое разложение: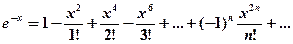
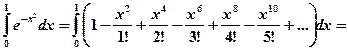
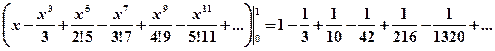
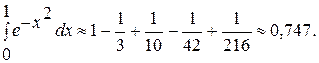
 .
.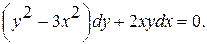
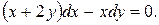
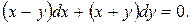

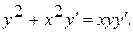
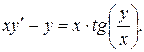
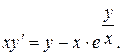
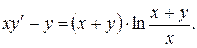
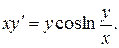
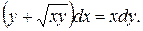
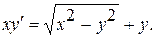
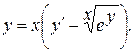
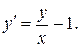
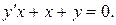
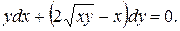
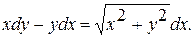
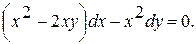
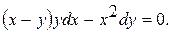
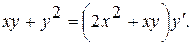
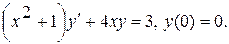
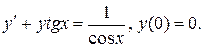
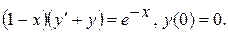
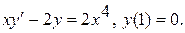
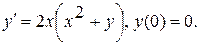
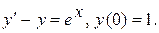
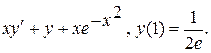

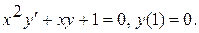
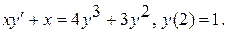
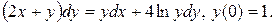
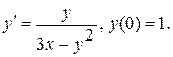
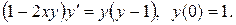
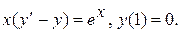
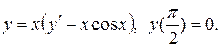
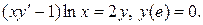
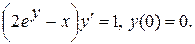
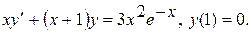
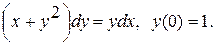
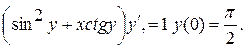
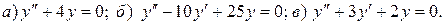
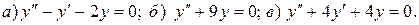
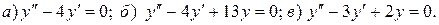
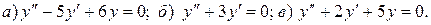
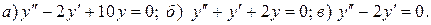
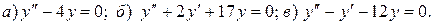
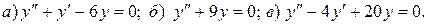

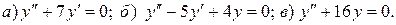
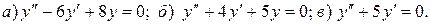

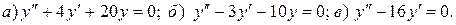
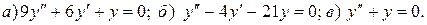
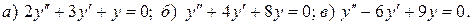
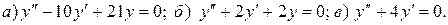
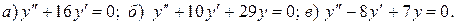
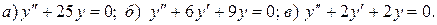

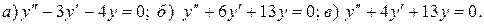
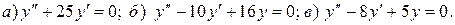
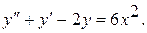 11.
11. 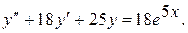
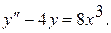 12.
12. 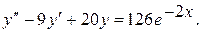
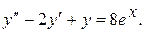 13.
13. 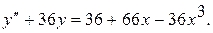
 14.
14. 
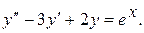 15.
15. 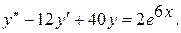
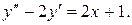 16.
16. 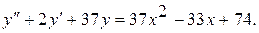
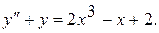 17.
17. 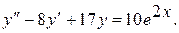
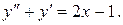 18.
18. 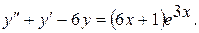
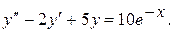 19.
19. 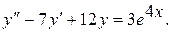
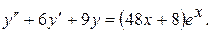 20.
20. 
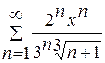 .
. .
. .
.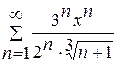 .
. .
.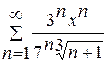 .
.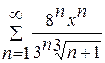 .
.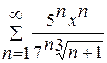 .
.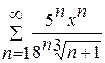 .
.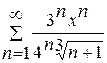 .
.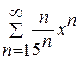 .
.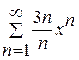 .
.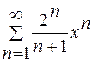 .
.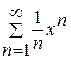 .
.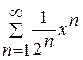 .
.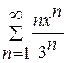 .
.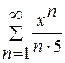 .
.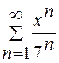 .
.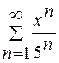 .
.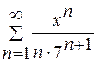 .
.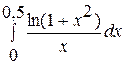 . 2.
. 2. 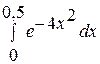 .
.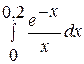 . 4.
. 4.  .
.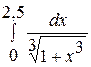 . 6.
. 6. 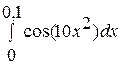 .
. . 8.
. 8. 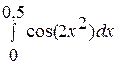 .
.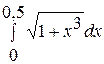 . 10.
. 10. 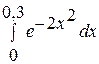 .
.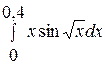 . 12.
. 12. 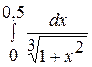 .
.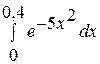 . 14.
. 14. 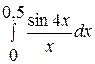 .
.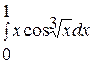 . 16.
. 16. 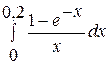 .
.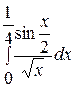 . 18.
. 18. 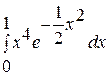 .
.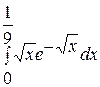 . 20.
. 20. 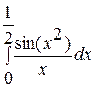 .
.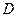 плоскости
плоскости 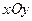 задана непрерывная функция
задана непрерывная функция 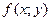 .Разобьём область
.Разобьём область 
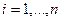 , площади которых обозначим через
, площади которых обозначим через  , а диаметры (наибольшее расстояние между точками области) через
, а диаметры (наибольшее расстояние между точками области) через 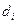 .
.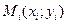 , умножим значение
, умножим значение 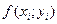 функции в этой точки на
функции в этой точки на 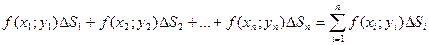
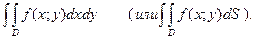

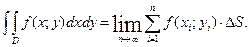
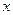 и
и 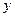 - переменные интегрирования;
- переменные интегрирования;  или
или 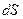 - элемент площади.
- элемент площади.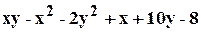 .
.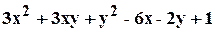 .
.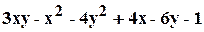 .
. .
.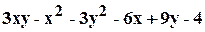 .
.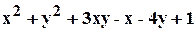 .
.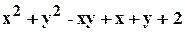 .
.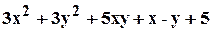 .
.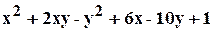 .
.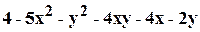 .
.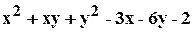 .
.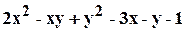 .
.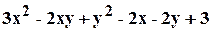 .
. .
. .
.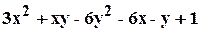 .
.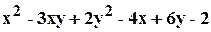 .
.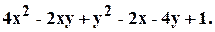
 .
.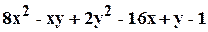 .
. Задание 8. Задана функция z= f (x, y). Найти градиент и производную этой функции в заданной точке М(х0, у0) в направлении вектора l, составляющего угол a с положительным направлением оси Ох.
Задание 8. Задана функция z= f (x, y). Найти градиент и производную этой функции в заданной точке М(х0, у0) в направлении вектора l, составляющего угол a с положительным направлением оси Ох.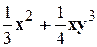 , M(1,-1), a=
, M(1,-1), a= 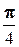 .
.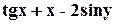 , M(
, M(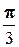 ), a=
), a= 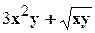 , M(2,-2), a=
, M(2,-2), a= 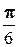 .
.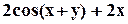 , M(
, M(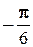 ), a=
), a= 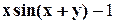 , M(
, M(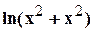 , M(3,4), a=
, M(3,4), a=  , M(1,-2), a=
, M(1,-2), a= 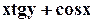 , M(
, M(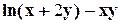 , M(1,-1), a=
, M(1,-1), a= 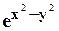 , M(2,-2), a=
, M(2,-2), a=  .
.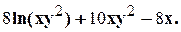
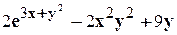 .
.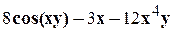 .
.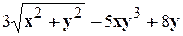 .
.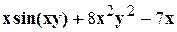 .
.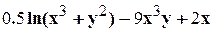 .
.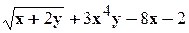 .
.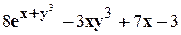 .
.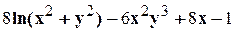 .
.