
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проектирование манипуляторов валочно-пакетирующих машинСодержание книги Поиск на нашем сайте
Задание: 1. Провести сравнительный анализ различных схем манипуляторов и выбрать вариант, обладающий наибольшей жесткостью. 2. Разработать компоновочно-кинематическую схему манипулятора валочно-пакетирующей машины. 3. Определить основные проектные параметры манипулятора (длины стрелы и рукояти). 4. Разработать расчетную схему нагрузок, действующих на манипулятор для заданного расчетного случая. Исходные данные: 1. Максимальный вылет манипулятора L = 7 м. 2. Максимальная высота укладки дерева в кониковое зажимное устройство 3. Расчетное дерево диаметром на высоте груди D = 50 см. 4. Коэффициент динамичности Выполнение задания: 1. Выбор схемы манипулятора лесной машины весьма ограничен и по существу сводится к анализу двух схем, показанных на рис. 1.12, или их комбинаций.
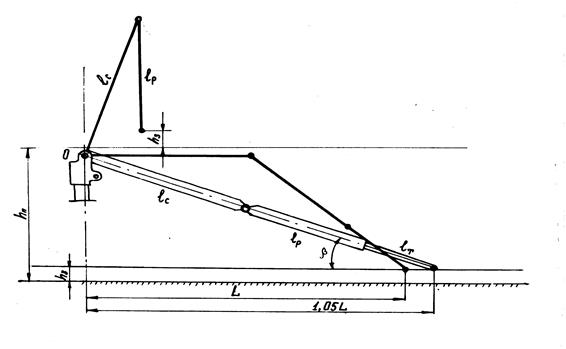
Шарниро-сочлененная конструкция А обладает большей жесткостью, нежели телескопическая конструкция Б. Однако при большом вылете усложняется компоновка стрелы с рукоятью (требуется большая длина стрелы). Для упрощения компоновки введем телескопическое звено рукояти длиной 1,5 м. 2. Важнейшим требованием, которым должна отвечать компоновочно-кинематическая схема, является требование перевода точки захвата на конце рукояти из положения на земле в положение над коником. Поэтому вначале построим общую кинематическую схему, показанную на рис. 1.13 (звенья манипулятора пока неизвестны). Составим уравнение длин в предположении, что стрела и рукоять над коником занимают близкое к вертикальному положение:
Имея в виду, что
получим
Преобразуем это уравнение:
или
Решая квадратное уравнение относительно длины рукояти, получим
Пусть
Суммарная длина звеньев манипулятора
Компоновочная схема разрабатывается на основе кинематической. В частности, такой важный проектный параметр, как высота шарнира О, найден как
Здесь принята высота рабочего органа hк = hо + hпл. Итак, все проектные параметры манипулятора найдены. Эти параметры обеспечивают перенос комля дерева с расстояния 7 м от оси колонны на высоту В качестве расчетного случая нагрузок принимаем случай подъема дерева на максимальном вылете, полагая, что трактор стоит на горизонтальной поверхности. В этом случае имеем плоское нагружение конструктивных элементов. Изобразим в некотором масштабе положение стрелы и манипулятора в момент подъема дерева на некоторую высоту Что касается нагрузки на конце манипулятора, то она слагается из силы тяжести части дерева в захвате, определяемой коэффициентом n, и силы тяжести захватно-срезающего устройства. Масса дерева находится по заданному диаметру с помощью графиков (рис. 1.4, 1.5). Масса ЗСУ должна быть задана. В первом приближении ее можно принять равной 800 кг при валке деревьев на земле и 1500 кг при переносе деревьев в вертикальном положении. Силы тяжести стрелы и рукояти также можно задать ориентировочно по статистическим данным.
Учет динамичности нагрузок можно осуществить двояко: можно умножить на
1.7. Выбор оптимальных точек подвеса гидроцилиндров
Задание: 1. Разработать расчетную схему для определения положения проушин сочленения гидроцилиндров со стрелой, рукоятью и поворотной колонной. 2. Разработать алгоритм расчета координат шарниров сочленения гидроцилиндра управления стрелой. 3. Разработать алгоритм оптимизации точек подвеса заданного гидроцилиндра к стреле и колонне. 4. Проанализировать решение задачи оптимизации на ЭВМ.
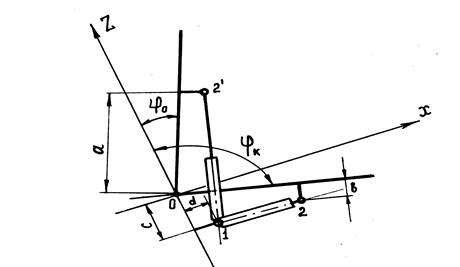
Исходные данные: 1. Длина гидроцилиндра с втянутым штоком 2. Ограничения на размещение проушин: шарнир подвеса штока к стреле должен отстоять от линии OOp (рис. 1.15) на расстоянии b, а шарнир подвеса цилиндра к колонне на расстоянии d от осевой линии колонны, проходящей через шарнир О. 3. Предельные значения углов поворота стрелы Выполнение задания. 1. Расчетная схема представлена на рис. 1.15 (свяжем с основным шарниром О неподвижную систему координат OXZ). Определим координаты точек 1, 2, 2' в принятой системе координат.
Координаты точек подвеса гидроцилиндра стрелы зависят от четырех проектных параметров, два из которых заданы и два подлежат определению.
2. Алгоритм расчета координат подвеса гидроцилиндра к стреле строится на основе краевых условий:
Длины отрезков
Имея это в виду, получаем следующие данные функциональной зависимости:
В данном случае задача поиска координат подвеса гидроцилиндра к стреле оказалась замкнутой – два неизвестных " а " и " b " должны определяться из двух линейно-независимых уравнений. Однако аналитическое решение этих двух нелинейных уравнений затруднено громоздкими выкладками. Поэтому эти уравнения целесообразно решать на ЭВМ. 3. Алгоритм поиска решения строим путем итераций. Задаемся величиной С и решаем первое уравнение относительно а:
Подставляем найденное решение во второе уравнение и находим невязку ∆ Поиск искомого решения сводится к минимизации невязки ∆(C) на ноль. При этом алгоритм поиска решения записывается в виде min ∆(C) = 0, C где С принадлежит некоторой области G (области варьирования с некоторым шагом ∆C). В данном случае минимизация функции невязки не есть оптимизация параметров, а представляет собой всего лишь процедуры численного поиска решения нелинейной системы алгебраических уравнений. Однако условно решение можно считать оптимальным в том смысле, что рабочий ход используется максимально. 4. До сих пор положение точек подвеса находилось для заданного гидроцилиндра величинами Плечо силы
Это следует из того, что модуль векторного произведения Но знаменатель дроби равен длине гидроцилиндра с втянутым штоком
Алгоритм поиска оптимального решения сводится к следующему: 1) Задаемся рядом гидроцилиндров совокупностью 2) Для каждой пары значений 3) Среди множества решений оставляем то, при котором Символически поиск оптимального решения можно записать в виде
где а и с есть функции Область Г может быть ограничена непосредственно диапазонами
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.77.51 (0.011 с.) |

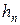 = 3 м.
= 3 м.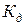 = 1,4.
= 1,4.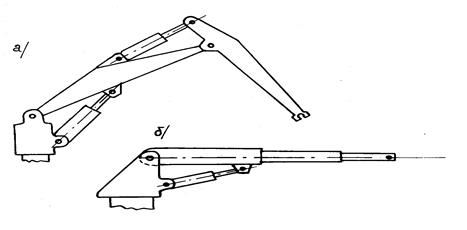
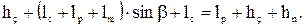
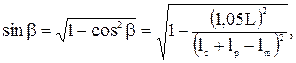
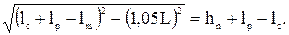
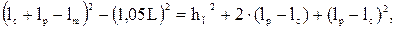
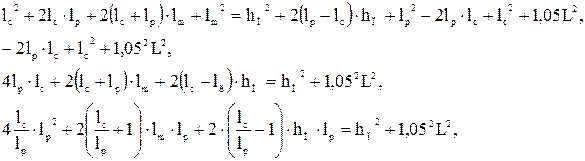
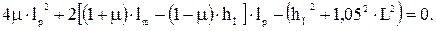
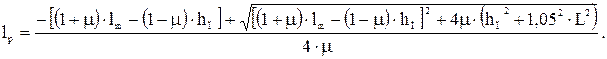
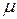 = 1, тогда
= 1, тогда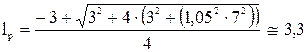 м,
м,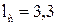 м.
м.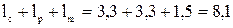 м.
м.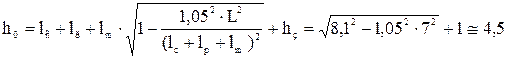 м.
м.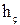 = 1 м. Зная высоту площадки hпл под поворотную колонну, находим высоту колоны
= 1 м. Зная высоту площадки hпл под поворотную колонну, находим высоту колоны 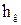 :
: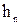 = 3 м над коником.
= 3 м над коником.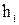 (рис. 1.14). Для определения эпюр изгибающих моментов, нормальных и касательных сил необходимо знать усилия на штоках гидроцилиндров, а для этого необходимо задаться компоновкой гидроцилиндров. Задаемся расстоянием между точками Op 4 и координатами точек 1, 2, 3. Координаты точек 2, 3 задают относительно линии OOp (расстоянием вдоль этой линии и расстоянием по перпендикуляру к этой линии), а координаты точки 1 задают относительно осевой линии колонны, проходящей через точку О. При задании положения точек 1, 2, 3 необходимо стремиться к тому, чтобы проушины располагались вне конструкции (в противном случае, будет иметь место ослабление сечений). Но размеры сечений пока неизвестны. Поэтому приходится прорабатывать несколько вариантов подвеса гидроцилиндров. При этом возникает проблема оптимизации гидропривода.
(рис. 1.14). Для определения эпюр изгибающих моментов, нормальных и касательных сил необходимо знать усилия на штоках гидроцилиндров, а для этого необходимо задаться компоновкой гидроцилиндров. Задаемся расстоянием между точками Op 4 и координатами точек 1, 2, 3. Координаты точек 2, 3 задают относительно линии OOp (расстоянием вдоль этой линии и расстоянием по перпендикуляру к этой линии), а координаты точки 1 задают относительно осевой линии колонны, проходящей через точку О. При задании положения точек 1, 2, 3 необходимо стремиться к тому, чтобы проушины располагались вне конструкции (в противном случае, будет иметь место ослабление сечений). Но размеры сечений пока неизвестны. Поэтому приходится прорабатывать несколько вариантов подвеса гидроцилиндров. При этом возникает проблема оптимизации гидропривода.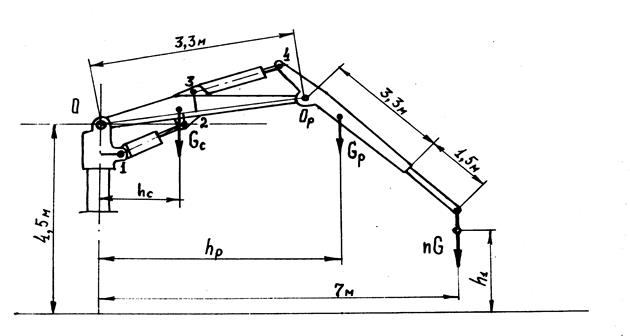
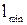 , длина гидроцилиндра со штоком
, длина гидроцилиндра со штоком 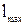 .
.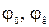 .
.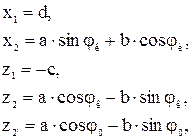
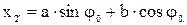
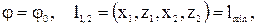
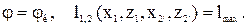
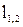 и
и 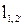 через координаты определяются по формулам
через координаты определяются по формулам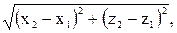
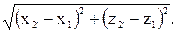
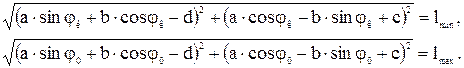
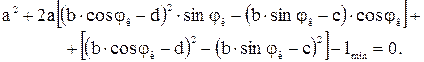
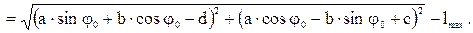
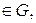
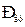 через координаты определяется следующим выражением:
через координаты определяется следующим выражением: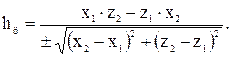
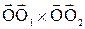 равен удвоенной площади треугольника OO1O2, которая в свою очередь равна произведению O1O2
равен удвоенной площади треугольника OO1O2, которая в свою очередь равна произведению O1O2 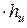 .
.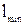 (по условию задачи). Таким образом, имеем:
(по условию задачи). Таким образом, имеем: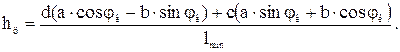
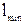 ,
, 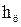 .
.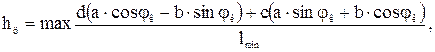
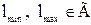 ,
,


