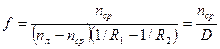В центре картины наблюдаются то минимумы, то максимумы.

Амплитуде дифрагированной волны в точке P соответствует вектор AB, показанный на фазовой диаграмме. Как будет изменяться интенсивность в точке P по мере увеличения диаметра отверстия до размера, которому будет соответствовать вектор амплитуды AC?

Будет сначала возрастать, а затем убывать

На экране P наблюдается дифракция Френеля на круглом отверстии D от точечного монохроматического источника S. Оцените (в миллиметрах) диаметр отверстия, если SD = 1 м, DP = 2 м, а длина волны 0.5 мкм.

2) 2.0

Плоская монохроматическая волна (расстояние a велико, лямбда = 450 нм) с интенсивностью J0 падает по нормали на круглое отверстие с R = 1.2 мм. Найти интенсивность в точке P при b = 3.2 м. Амплитуде в точке P соответствует один из векторов, показанных на векторной диаграмме.

5) 4 * J0

Наблюдается дифракция плоской монохроматической волны на полубесконечном непроницаемом экране. Введите номер правильного варианта распределения интенсивности света вдоль оси x.

3)

Монохроматическая волна интенсивностью J0 падает на круглое отверстие диаметра d, открывающего для точки наблюдения P одну зону Френеля. Определите, во сколько раз интенсивность в точке P больше, чем J0? (амплитуде в точке P соответствует один из векторов, показанных на фазовой диаграмме)

J0

Точечный монохроматический источник S освещает непрозрачный диск D. На экране P в центре геометрической тени наблюдается светлое пятно (т. н. пятно Пуассона). Определите, что будет происходить с картиной на экране при постепенном увеличении диаметра диска.

Пятно будет бледнеть, оставаясь светлее тени.

На экране Р наблюдается дифракция Френеля на круглом отверстии D от точечного монохроматического источника S. Определите число открытых зон Френеля по заданному распределению интенсивности в плоскости экрана вдоль оси х.

3)

 

 

Формулы.

 

уравнение Гельмгольца для поля монохроматической световой волны, распространяющейся в немагнитной среде (m=1) с показателем преломления n; k_o=2 p/l _o – волновой вектор, обратный длине волны

 

(grad L)²= n ²

уравнение эйконала (оптического пути), где L = const – геометрический волновой фронт

 

d s= d L/n

расстояние между соседними волновыми фронтами увеличивается по мере уменьшения показателя преломления, и наоборот; во всех средах (n >1) d L >d s

оптический путь между двумя точками равен скорости света в вакууме, умноженной на время прохождения лучом расстояния между этими точками

 

в неоднородной среде световые лучи изгибаются в сторону увеличения показателя преломления

 

n ₁sina= n ₂sinb

закон Снеллиуса: луч преломлённый лежит в плоскости падения, а синусы углов падения и преломления связаны отношением показателей преломления

 

sina= n ₂/ n ₁

угол падения, при котором возникает эффект полного внутреннего отражения (ПВО)

 

зависимость минимального угла отклонения s_min от показателя преломления призмы n и угла в вершине призмы q; угол s минимален в случае симметрического хода лучей (a₁=a₂)

 

инвариант Аббе для прохождения лучами раздела сред линза-среда; R – радиус кривизны раздела сред; a ₁ – геометрический ход луча в среде, a ₂ – геометрический ход луча в линзе

 

формула сферической преломляющей поверхности

 

оптическая сила сферической преломляющей поверхности

 

переднее фокусное расстояние сферической преломляющей поверхности

 

заднее фокусное расстояние сферической преломляющей поверхности

 

фокусные расстояния прямо пропорциональны показателям преломления сред, у которых они расположены

 

оптическая сила сферического зеркала

 

линейное или поперечное увеличение – отношение размера изображения к размеру предмета

 

формула тонкой линзы в среде

 

оптическая сила тонкой линзы

 

фокусное расстояние тонкой линзы