Чему равна амплитуда колебаний, возбужденных в точке наблюдения, если в круглом отверстии в непрозрачном экране укладывается четное число зон Френеля.

Eφ=E1+E2+E3+…+EN=Emφcosωt

Iφ = αE²mφ

 

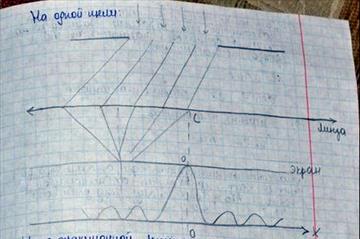
При четном числе 2,4,6…2m, где m=1,2,3, амплитуда Emφ=0, и интенсивность света на экране будет минимальна: Imin=0

Чему равна амплитуда колебаний, возбужденных в точке наблюдения, если в круглом отверстии в непрозрачном экране укладывается нечетное число зон Френеля?

При нечетном числе N=3,5,7…(2n+1), где n=1,2,3…, амплитуда вектора напряженности электрического поля Emφ= Em1 ~ Em/N, обеспечивает максимально интенсивность света на экране

Imax = αE²mφ ~Iв/N²

Запишите условие возникновения максимумов при дифракции Фраунгофера на одной щели.

При N=2n+1, из формулы b*sinφ=N*λ/2

(т.к. l= λ/2, и l=S*sinφ = (b/N)*sinφ.) следует условие дифракционных максимумов (Imax):

b*sinφ= ± (n + ½)λ, где n=1,2,3… - порядок максимума

Запишите условие возникновения минимумов при дифракции Фраунгофера на одной щели.

При N=2m из формулы b*sinφ=Nλ/2,

Получим условие дифракционных минимумов (Imin):

b*sinφ= ±mλ

От чего зависит ширина центрального максимума при дифракции на одной щели?

При угле дифракции φ=0 в точке х=0 экрана будет наблюдаться наиболее интенсивный (I0= αE²mφ~Ib) центральный максимум.

Координаты минимумов или максимумов х=Fsinφ.

xm= ± m*λ/b*F

xn= ± (2m+1)*λ/2b*F

Ширина центрального максимума, ограниченная минимумами порядка m=1, определяется зависимостью:

x0=2* λ/b*F

Она увеличивается при уменьшении ширины щели b, что не может быть объяснено законами геометрической оптики

L>> b²/λ. На экране, достаточно удаленном от щели, дифракцию Фраунгофера можно наблюдать и без собирающей линзы.

Тогда х = L*sinφ ~ ˪ tgφ

xm= ± m*λ/b*L

xn= ± (2n+1)*λ/2b*L

В чем заключается существенная разница между дифракционными картинами, полученными при дифракции на одной щели и нескольких щелях?

Дифракционная решетка – периодическая система параллельных щелей в преграде, имеющих одинаковую ширину b и расположенных на одинаковом расстоянии а от друг друга

Дифракционные решетки создают эффект резкого разделения и усиления интенсивности света в области максимумов, что делает их незаменимыми оптическими приборами. Они позволяют получать ярко выраженную дифракционную картину.

Главные максимумы интенсивности света:

dsinφn = ± kλ EmN = NEmφ

Интенсивность света IN = αE²mφ ~ N²/Iφ

Из этой формулы видно, что дифракционная решетка позволяет резко (в N² раз) усилить интенсивность света в области максимумов по сравнению с картиной дифракции на одной щели

Запишите условие возникновения главных максимумов при дифракции Фраунгофера на нескольких одинаковых параллельных щелях (дифракционной решетке).

l=d*sinφ

dsinφk = ±kλ – главные максимумы