
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Результати статистичної обробки розподілу довжини (середнього поперечного розміру) зерна.Содержание книги
Поиск на нашем сайте
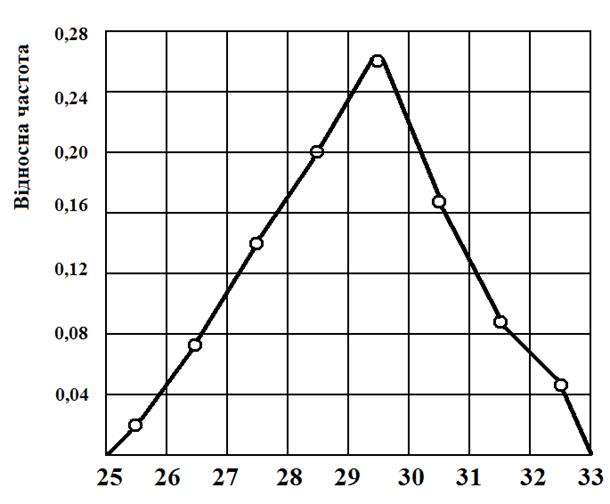
12. Для побудови варіаційних кривих будуються координатні осі XOY. На осі Х відкладаються значення класів від L(min) до L(max), причому L(min) повинно співпадати з точкою перетину осі OY з віссю OX, а на осі Y відкладаються значення відносної частоти P(k). Зразок побудови гістограм вибірки і варіаційних кривих представлений на рис. 2.1. та рис. 2.2. 13.Скласти звіт по лабораторній роботі.
Рис. 2.1. Приклад побудови гістограми вибірки
Зміст звіту 1. По даним лабораторної роботи №1 зробити розрахунки статистичних параметрів згідно з пп.. 1...11. 2. Заповнити таблицю результатів статистичних розрахунків. 3. На аркуші ф. А4 міліметрового паперу побудувати варіаційні крив і гістограми розподілу довжини і середнього поперечного розміру. Графіки статистичного розподілу вклеїти до звіту.
Рис. 2.2. Приклад побудови варіаційної кривої
Контрольні питання для самостійної роботи 1. Яка величина точності досліду є допустимою при дослідженні розмірно-масових характеристик сільськогоспо-дарських культур? 2. До якої функції наближається форма варіаційної кривої при безкрайньому збільшенні об’єму вибірки? 3. Чим відрізняється середньостатистичне значення параметру, що вивчається від середньоарифметичного значення?
Література: 1. Яковлев К.П. Математическая обработка результатов измерений. М., Наука. 1985 г. 2. Львовский Е.Н. Статистические методы построения эмпирических формул. М.., Высшая школа,1988 г. 3. Бродский А.Д., Кан.В.Л. Краткий справочник по матема-тической обработке результатов измерений. М., Наука, 1976 г. 4. Касандрова О.Н., Лебедев В.В. обработка результатов наблюдений. М., Наука, 1987 г.
Лабораторна робота №3 „Застосування методу найменших квадратів при вивченні взаємопов’язаних розмірних параметрів” Мета роботи: 1. Навчитися використовувати метод найменших квадратів при вивченні взаємопов’язаних параметрів, що характеризують сільськогосподарські культури; 2. Оволодіти методикою отримання функціональних залежностей по результатах спостережень і побудовою графіків отриманих залежностей.
Технічне забезпечення роботи: Мікрокалькулятор МК-51, МК-52, будь-який сучасний комп’ютер.
Порядок виконання роботи: 1. По результатах лабораторних робіт 1; 2 заповнити табл. 3.1. Таблиця 3.1 Вихідні данні для розрахунку функціональних залежності
2. Для отримання лінійної функціональної залежності довжини насіння від його середнього поперечного розміру, що має вид:
необхідно визначити величини коефіцієнтів А і В. Для знаходження значень коефіцієнтів необхідно рішити систему рівнянь (3.2)
де L(k); a(cp.k) – значення довжини і середнього поперечного розміру з k-го рядка табл. 3.1. N- число класів. 3. Після знаходження значень коефіцієнтів А і В, підставляючи в формулу 3.1 значення a (cp.k) з табл. 3.1, розрахувати теоретичне значення величини довжини зерна L(k)'. Результати розрахунків занести в табл. 3.2. Таблиця 3.2 Результати апроксимації експериментальних даних Лінійною залежністю
4. Дисперсія відхилень між теоретичними значеннями і результатами експериментальних даних по кожному з класів знаходиться як: D(k)'=[L(k)'-L(k)]2 (3.3) а дисперсія по всій сукупності апроксимації експериментальних даних:
5. Визначити значення критерії Фішера, що визначає адекватність опису отриманою лінійною математичною залежністю результатів експериментальних даних. Розрахункове значення критерії Фішера дорівнює:
6. Порівняйте розрахункове значення критерії Фішера з табличним значенням F(T), що наведено в додатку 1. Втому випадку якщо F(p) < F(T) гіпотеза про адекватність опису математичною моделлю результати експериментальних досліджень приймається; в противному – відкидається. 7. Нa координатних осях a(cp.); 0; L відкласти точки L(k), відповідні a(cp.k). На цих же координатних осях побудувати залежність 8. Скласти звіт по лабораторній роботі.
Зміст звіту 1. По даним лабораторних робіт №1;2 заповнити табл. 3.1. 2. Зробити розрахунок коефіцієнтів А, і В, необхідних для побудови функціональної залежності, в відповідності з п. 2,3. 3. Розрахувати коефіцієнт Фішера, порівняти розрахункове значення з табличним. 4. Заповнити табл. 3.2. 5. На ф. А4 міліметрового паперу побудувати графічні залежності довжини насіння від середнього поперечного розміру.
Рис. 3.1 Приклад побудови лінійної функціональної залежності
Зміст звіту 5. По даним лабораторних робіт № 1 та № 2 заповнити табл. 3.1. 6. Зробити розрахунок коефіцієнтів А, і В, які є необхідні для побудови функціональної залежності, в відповідності з п. 2.3. 7. Розрахувати коефіцієнт Фішера, порівняти розрахункове значення з табличним. 8. Заповнити табл. 3.2. 9. На ф. А4 міліметрового паперу побудувати графічні залежності довжини насіння від середнього поперечного розміру.
Контрольні питання для самостійної роботи: 1. Що таке довірчий інтервал апроксимації експериментальних даних і яка його величина при дослідженні сільськогосподарських процесів? 2. На основі якого математичного методу здійснюється розрахунок коефіцієнтів математичної моделі? В чому його суттєвість? 3. Чому на графіці L=f [a(cp)] пряма не співпадає зі всіма крапками експериментальних значень?
Література: 1. Яковлєв К.П. Математическая обработка результатов. М., Наука. 1985 г. 2. Львовский Е.Н. Статические методы построения эмпирических формул. М., Высшая школа, 1988 г. 3. Мельников С.В. и др. Планирование эксперимента в исследованиях сельскохозяйственных процессов. Л., Колос, 1980 г.
Лабораторна робота №4 „Апроксимація експериментальних даних квадратичною функціональною залежністю”
Мета роботи: 1. Вивчити методику розрахунку коефіцієнтів квадратного рівняння, при використанні методу найменших квадратів для опису результатів досліду. 2. Навчитися побудові графічних залежностей.
Технічне забезпечення роботи: мікрокалькулятор МК-51, МК-52; будь-який сучасний комп’ютер.
Порядок виконання роботи: 1. По результатах лабораторних робіт №1 та № 2 заповнити табл. 4.1. 2. Для отримання квадратичної функціональної залежності довжини насіння від його середнього поперечного розміру, що приймає вигляд:
необхідно визначити величини коефіцієнтів А, В і С. Для знаходження значень коефіцієнтів необхідно вирішити систему рівнянь (4.2):
де L(k); a(cp.k) – значення довжини і середнього поперечного розміру з „k”-того рядка табл. 4.1. N - число класів. 3. Після знаходження значень коефіцієнтів А, В і С, підставляючи у формулу 4.1. значення a(cp.k) з табл.4.1, розрахувати теоретичні значення величини довжини зерна L(k)'. Результати розрахунків занести в табл. 4.2. Таблиця 4.1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.52.54 (0.007 с.) |


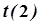 ; Дисперсія D;
Коефіцієнт варіації
; Дисперсія D;
Коефіцієнт варіації  ; Точність досліду f;
..................
; Точність досліду f;
..................
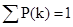



 (3.1)
(3.1) (3.2)
(3.2) (3.4)
(3.4)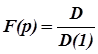 (3.5)
(3.5) . Приклад побудови функціональної залежності наведений на рис. 3.1.
. Приклад побудови функціональної залежності наведений на рис. 3.1.

 (4.1)
(4.1) (4.2)
(4.2)


