
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа силы упругости пружины.
РАЗДЕЛ 3. ДИНАМИКА. Работа и мощность сил Работа силы — скалярная мера действия силы. 1. Элементарная работа силы. Элементарная работа силы — это бесконечно малая скалярная величина, равная скалярному произведению вектора силы на вектор бесконечного малого перемещения точки приложения силы:
В (3.37)
Так как
т. е. работу совершает только касательная сила, а работа нормальной силы равна нулю. Из (3.38) следует: если 2. Аналитическое выражение элементарной работы. Представим векторы
3. Работа силы на конечном перемещении равна интегральной сумме элементарных работ на этом перемещении
или
Если сила постоянная, а точка ее приложения перемещается прямолинейно, то
Например, дано:
Работа силы тяжести не зависит от формы траектории. При движении по замкнутой траектории ( Работа силы упругости пружины.
где
а) Работа внутренних сил
Элементарная работа всех внутренних сил в твердом теле равна нулю:
Следовательно, на любом конечном перемещении тела
б) Работа внешних сил. Поступательное движение тела. Элементарная работа где
Элементарная работа Элементарная работа всех внешних сил
где Работа сил на конечном перемещении
Если где 7. Мощность — это работа, выполненная силой в единицу времени. Если работа совершается равномерно, то мощность
где В более общем случае мощность силы можно определить как отношение элементарной работы силы
8. Коэффициент полезного действия (КПД)
9. Единицы измерения работы и мощности. В системе СИ единица измерения работы силы — джоуль (1 Дж= 1 Н м),а в системе МкГС — кГм. Единица измерения мощности — соответственно — ватт (1 Вт = 1 Дж/с) и кГм/с. 75 кГм/с = 1 л. с. (лошадиная сила). 1 кВт= 1000 Вт = 1,36 л. с. Теорема Кенига Кинетическая энергия механической системы в общем случае ее движения равна сумме кинетической энергии движения системы вместе с центром масс и кинетической энергии системы при ее движении относительно центра масс:
где РАЗДЕЛ 3. ДИНАМИКА. Работа и мощность сил Работа силы — скалярная мера действия силы. 1. Элементарная работа силы. Элементарная работа силы — это бесконечно малая скалярная величина, равная скалярному произведению вектора силы на вектор бесконечного малого перемещения точки приложения силы:
В (3.37)
Так как
т. е. работу совершает только касательная сила, а работа нормальной силы равна нулю. Из (3.38) следует: если 2. Аналитическое выражение элементарной работы. Представим векторы
3. Работа силы на конечном перемещении равна интегральной сумме элементарных работ на этом перемещении
или
Если сила постоянная, а точка ее приложения перемещается прямолинейно, то
Например, дано:
Работа силы тяжести не зависит от формы траектории. При движении по замкнутой траектории ( Работа силы упругости пружины.
где
а) Работа внутренних сил
Элементарная работа всех внутренних сил в твердом теле равна нулю:
Следовательно, на любом конечном перемещении тела
б) Работа внешних сил. Поступательное движение тела. Элементарная работа где
Элементарная работа Элементарная работа всех внешних сил
где Работа сил на конечном перемещении
Если где 7. Мощность — это работа, выполненная силой в единицу времени. Если работа совершается равномерно, то мощность
где В более общем случае мощность силы можно определить как отношение элементарной работы силы
8. Коэффициент полезного действия (КПД)
9. Единицы измерения работы и мощности. В системе СИ единица измерения работы силы — джоуль (1 Дж= 1 Н м),а в системе МкГС — кГм. Единица измерения мощности — соответственно — ватт (1 Вт = 1 Дж/с) и кГм/с. 75 кГм/с = 1 л. с. (лошадиная сила). 1 кВт= 1000 Вт = 1,36 л. с.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.18.59 (0.007 с.) |
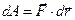 (3.37)
(3.37) — приращение радиуса-вектора
— приращение радиуса-вектора  точки приложения силы, годографом которого является траектория этой точки. Элементарное перемещение
точки приложения силы, годографом которого является траектория этой точки. Элементарное перемещение 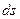 точки по траектории совпадает с
точки по траектории совпадает с  (3.38)
(3.38)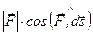 — проекция силы на направление перемещения точки (при криволинейной траектории — на касательную ось
— проекция силы на направление перемещения точки (при криволинейной траектории — на касательную ось  к траектории), то
к траектории), то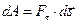 (3.39)
(3.39) ,то
,то  ; если
; если  ,то
,то  ; если
; если  ,то
,то  .
. и
и  ,
,  и подставим в (3.37). Получим
и подставим в (3.37). Получим |. (3.40)
|. (3.40) (3.41)
(3.41) |. (3.42)
|. (3.42)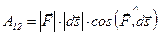 (3.43)
(3.43) ,
, 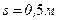 ,
,  .
. 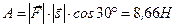 .
. 4. Работа силы тяжести (рис. 17). Используем формулу (3.42):
4. Работа силы тяжести (рис. 17). Используем формулу (3.42): 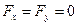 ,
,  ;
;  , где
, где  — перемещение точки приложения силы по вертикали вниз (высота).
— перемещение точки приложения силы по вертикали вниз (высота). При перемещении точки приложения силы тяжести вверх
При перемещении точки приложения силы тяжести вверх  (точка
(точка  — внизу,
— внизу,  — вверху). Итак,
— вверху). Итак,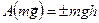 (3.44)
(3.44)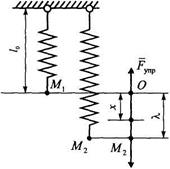

 Пружина растягивается только вдоль оси
Пружина растягивается только вдоль оси  (рис. 18). Используем (3.42):
(рис. 18). Используем (3.42): 
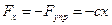 ;
; 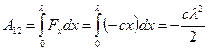 , где
, где 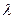 — величина деформации пружины. При перемещении точки приложения силы
— величина деформации пружины. При перемещении точки приложения силы 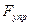 из нижнего положения в верхнее направление силы и направление перемещения совпадают, тогда работа силы упругости дается формулой
из нижнего положения в верхнее направление силы и направление перемещения совпадают, тогда работа силы упругости дается формулой (3.45)
(3.45) Примечание. При перемещении точки приложения силы упругости по криволинейной траектории из положения
Примечание. При перемещении точки приложения силы упругости по криволинейной траектории из положения  , (3.46)
, (3.46) ,
,  — деформации пружины в этих положениях.
— деформации пружины в этих положениях.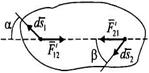 6. Работа сил, приложенных к твердому телу.
6. Работа сил, приложенных к твердому телу. Для двух
Для двух 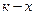 точек:
точек:  . (рис. 20).
. (рис. 20). . (3.47)
. (3.47)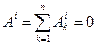 (3.48)
(3.48) силы
силы 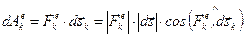 . Для всех сил
. Для всех сил  . Так как при поступательном движении
. Так как при поступательном движении  , то
, то  , (3.49)
, (3.49) — проекция главного вектора внешних сил на направление перемещения. Работа сил на конечном перемещении
— проекция главного вектора внешних сил на направление перемещения. Работа сил на конечном перемещении 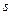
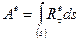 , (4.50)
, (4.50) Вращение тела вокруг неподвижной оси (рис. 21).
Вращение тела вокруг неподвижной оси (рис. 21). Элементарная работа
Элементарная работа  , где
, где  — составляющие силы
— составляющие силы  по естественным осям
по естественным осям  . Так как
. Так как  , то работа этих сил на перемещение
, то работа этих сил на перемещение 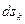 точки приложения силы равна нулю. Тогда
точки приложения силы равна нулю. Тогда  , но
, но 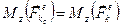 .
.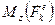 на элементарный угол поворота
на элементарный угол поворота  тела вокруг оси.
тела вокруг оси. , (3.51)
, (3.51) — главный момент внешних сил относительно оси.
— главный момент внешних сил относительно оси.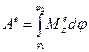 (3.52)
(3.52) , то
, то  (3.53)
(3.53) — конечный угол поворота;
— конечный угол поворота;  , где
, где 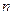 — число оборотов тела вокруг оси.
— число оборотов тела вокруг оси. (3.54)
(3.54) — работа, совершенная силой на конечном перемещении, за время
— работа, совершенная силой на конечном перемещении, за время 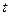 .
.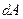 к элементарному промежутку времени
к элементарному промежутку времени  , за который совершена эта работа, что представляет собой производную от работы по времени. Поэтому
, за который совершена эта работа, что представляет собой производную от работы по времени. Поэтому (3.55)
(3.55) — отношение выполненной полезной работы
— отношение выполненной полезной работы  ко всей затраченной работе
ко всей затраченной работе  , т. е.
, т. е. (3.56)
(3.56) (3.59)
(3.59)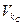 — скорость
— скорость  точки системы относительно центра масс.
точки системы относительно центра масс.


