Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что такое шарнир пластичности?Содержание книги Поиск на нашем сайте
После исчерпания упругой работы в сплошных изгибаемых элементах, выполненных из пластичных сталей, пластические деформации распространяются в глубь сечения (рис. 2.14) и в предельном состоянии пронизывают все сечение, образуя шарнир пластичности.
13. Запишите условие пластичности? s ef = Ryn
14. Доказать, что для прямоугольного сечения, коэффициент, учитывающий развитие пластических деформаций С1=1.5.
15. Как влияет образование шарнира пластичности на работу неразрезных балок? Для неразрезных балок образование шарнира пластичности приводит к перераспределению моментов и понижению степени статической неопределимости конструкции.
Запишите формулу обеспечения устойчивости сжатого элемента.
17. Запишите формулу обеспечения устойчивости изгибаемого элемента.
В каких случаях не требуется проверки общей устойчивости изгибаемого элемента? -при передаче нагрузки через сплошной жесткий настил, непре- рывно опирающийся на сжатый пояс балки и надежно с ним связанный (железобетонные плиты, плоский и профилированный металлический на- стил, волнистая сталь и т.п.); -при отношении расчетной длины балки lef к ширине сжатого пояса bf, не превышающем значений, определяемых табличными формулами [1].
Для каких стержней характерна потеря устойчивости? Гибких стержней
При достижении какой силы прямолинейная форма стержня перестает быть устойчивой? При достижении силой критического значения
Запишите формулу Л. Эйлера.
lef – расчетная длина стержня, зависящая от условий закреплений.
Запишите формулу критических напряжений.
Для каких деформаций справедлива формула Л. Эйлера? В пределах упругих деформаций
За счет чего может быть увеличена несущая способность стержня? путем увеличения момента инерции, без изменения площади поперечного сечения, путем размещения материала как можно дальше от главных осей инерции поперечного сечения.
С какой целью центрируется нагрузка сжатого стержня? Связь между прогибом и нагрузкой зависит в значительной степени от точности, с какой центрирована нагрузка
Когда стержень считается жестким, а когда гибким?
Запишите условие обеспечения устойчивости гибкого стержня.
Как определяется условная гибкость стержня?
29. Каким известным соотношением можно записать коэффициент Для стержней со сплошной стенкой значения условной гибкости l при вычислении коэффициента j по формулам из [1] определяется в трех случаях:
От каких условий зависит расчетная длина сжатого стержня (стойки)? Расчетная длина стержня зависит от условий его закрепления и определяется по формуле lef = lc m где lc – длина стойки; m – коэффициент приведения к расчетной длине, зависящий от способов закрепления стержня, например, с шарнирно опертыми концами стойки m = 1.
Сварные соединения
В чем заключается физический процесс сварки? Процесс сварки состоит в молекулярной диффузии металлов свариваемых изделий и плавящегося электрода, находящихся в жидком или высокопластичном состоянии и в совместной кристаллизации металлов при остывании.
2. Перечислите зоны сварного соединения. зона расплавления, зона термического влияния, весь остальной металл изделия
Дайте определение зоны термического влияния (ЗТВ). Прилегающий к шву участок основного металла, нагретого выше температуры 723 °С и ниже температуры расплавления 1535 °С называется зоной термического влияния
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 816; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.166.45 (0.007 с.) |

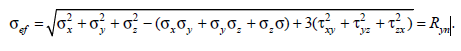
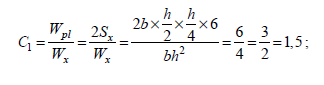 где Wpl = C 1 ´ Wx или C 1 = Wpl / Wx; С1 – коэффициент, учитывающий развитие пластических деформаций; Wpl – пластический момент сопротивлений; Wx – упругий момент сопротивлений.
где Wpl = C 1 ´ Wx или C 1 = Wpl / Wx; С1 – коэффициент, учитывающий развитие пластических деформаций; Wpl – пластический момент сопротивлений; Wx – упругий момент сопротивлений.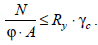
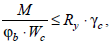 где Wc – следует определять для сжатого пояса; j b – следует определять согласно [1].
где Wc – следует определять для сжатого пояса; j b – следует определять согласно [1].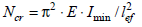 где E – модуль упругости; I min – минимальный осевой момент инерции;
где E – модуль упругости; I min – минимальный осевой момент инерции;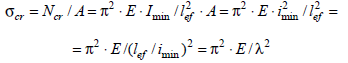
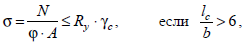 где А – площадь сечения; j – определяется по [1] в зависимости от условной гибкости l.
где А – площадь сечения; j – определяется по [1] в зависимости от условной гибкости l.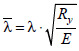 где l – гибкость, то есть l = lef / i; E – модуль упругости;
где l – гибкость, то есть l = lef / i; E – модуль упругости; 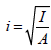 – радиус инерции; lef – расчетная длина стержня; А – площадь сечения; I – осевой момент инерции.
– радиус инерции; lef – расчетная длина стержня; А – площадь сечения; I – осевой момент инерции.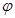 ?
?