
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плечом силы называется кратчайшее расстояние от оси вращения до линии действия силы.
Скалярная величина Просуммируем (23) по всем элементам массы тела:
Здесь Равенство (24) называется основным уравнением динамики вращательного движения. Т.к. скалярная величина J всегда положительная, то векторные величины Основное уравнение динамики вращательного движения по форме сходно с математическим выражением второго закона Ньютона:
Из сопоставления вытекает, что при вращательном движении роль силы играет момент силы (вращательный момент), а инертные свойства тела выражаются моментом инерции тела – J.
МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА Моментом импульса материальной точки относительно оси вращения называют векторную величину, модуль которой
Тогда момент импульса абсолютно твердого тела относительно неподвижной оси вращения
т.е. правление Запишем для нашего тела основное уравнение динамики вращательного движения в виде:
Если М = 0, то dL/dt = 0 т.е.
L = Jw = const. (28)
Момент импульса тела остается неизменным, если суммарный момент всех внешних сил действующих на тело равен нулю – это закон сохранения момента импульса. Для системы из N тел, которые вращаются вокруг общей оси, закон сохранения импульса записывается в виде:
МОМЕНТ ИНЕРЦИИ ТВЁРДЫХ ТЕЛ РАЗНОЙ ФОРМЫ ТЕОРЕМА ШТЕЙНЕРА Из определения момента инерции тел в общем виде:
следует, что эта величина является аддитивной. Это означает, что моменты инерции тел в некоторых случаях можно найти интегрированием исходя из геометрических соображений.
Масса этого элемента dm = r×S×d x, где r – плотность материала, S – площадь поперечного сечения. Момент инерции элемента массы dm:
но оси вращения 00', проинтегрируем левую часть () в пределах от 0 до J, а правую в пределах от 0 до l /2. Получим:
Т.к.
Т.к. r изменяется в пределах от r = 0 до r = R, то интегрируя получим:
но
Без выводов запишем: а) шар радиусом R и массой m, относительно оси, проходящей через его центр – б) полый тонкостенный цилиндр радиусом R и массой m, относительно его геометрической оси, параллельной образующей –
Согласно теореме Штейнера момент инерции тела – J относительно любой оси, параллельной оси проходящей через центр масс этого тела –
где J0 – момент инерции тела относительно оси, проходящей через центр масс, d – расстояние между осями. Например, если ось вращения проходит через конец стержня,
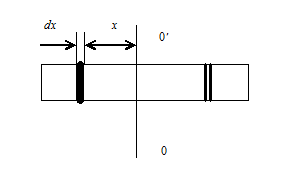
то В качестве примера Определим момент инерции J тонкого стержня длиной l, массой m и диаметром d<< l. Относительно оси
к стержню и проходящей через его центр масс. Выделим на расстоянии х от оси вращения элемент стержня бесконечно малой толщины d x. Масса этого элемента dm = r×S×d x, где r-плотность материала, S-площадь поперечного сечения. Момент инерции элемента массы dm
Интегрируем левую и правую части в пределах от 0 до J и правую от 0 до l /2. Учитывая, что элементы попарно симметричны, получим:
Т.к. б) диск или цилиндр радиусом R, высотой h и массой m. Определим момент инерции цилиндра относительно его геометрической оси, параллельной образующей.
Т.к. r изменяется в пределах от r = 0 до r = R, то интегрируя получим:
но
Без выводов запишем: а) тонкий однородный стержень –
б) диск или цилиндр радиусом R, высотой h и массой m -
Согласно теореме Штейнера момент инерции тела - J относительно любой оси, параллельной оси проходящей через центр масс этого тела
где J0 – момент инерции тела относительно оси через центр масс, d - расстояние между осями. Например, если ось вращения проходит через конец стержня,
то В качестве примера найдём момент инерции J тонкого стержня длиной l, массой m и диаметром d<< l. Относительно оси а) тонкий однородный стержень.
Выделим на расстоянии х от оси вращения элемент стержня бесконечно малой толщины d x. Масса этого элемента dm = r×S×d x, где r-плотность материала, S-площадь поперечного сечения. Момент инерции элемента массы dm
Интегрируем левую и правую части в пределах от 0 до J и правую от 0 до l /2. Учитывая, что элементы попарно симметричны, получим:
Т.к.
Определим момент инерции цилиндра относительно его геометрической оси, параллельной образующей. Выделим цилиндрический слой бесконечно малой толщины dr и радиусом r. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя
Т.к. r изменяется в пределах от r = 0 до r = R, то интегрируя получим:
но
Без выводов запишем: а) тонкий однородный стержень –
б) диск или цилиндр радиусом R, высотой h и массой m -
Согласно теореме Штейнера момент инерции тела - J относительно любой оси, параллельной оси проходящей через центр масс этого тела
где J0 – момент инерции тела относительно оси через центр масс, d - расстояние между осями. Например, если ось вращения проходит через конец стержня,
то Без выводов запишем: а) тонкий однородный стержень – ДОПОЛНИТЬ ВЫВОДОМ
б) диск или цилиндр радиусом R, высотой h и массой m -
Согласно теореме Штейнера момент инерции тела - J относительно любой оси, параллельной оси проходящей через центр масс этого тела
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.72 (0.006 с.) |
 называется момент инерции материальной точки относительно осивращения ZZ′.
называется момент инерции материальной точки относительно осивращения ZZ′. . Получим:
. Получим: или в векторном виде
или в векторном виде  (24)
(24) - результирующий момент силы, действующий на тело;
- результирующий момент силы, действующий на тело;  - момент инерции тела.
- момент инерции тела.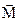 и
и  всегда направлены в одну сторону вдоль оси вращения тела.
всегда направлены в одну сторону вдоль оси вращения тела. ↔
↔ 
 .
.  (25)
(25) или в векторной форме
или в векторной форме  , (26)
, (26) лежит на оси вращения и совпадает по направлению с
лежит на оси вращения и совпадает по направлению с  (на-
(на- (27)
(27) . (29)
. (29) (30)
(30) В качестве примера найдём момент инерции J тонкого стержня длиной l, массой m и диаметром d << l относительно оси
В качестве примера найдём момент инерции J тонкого стержня длиной l, массой m и диаметром d << l относительно оси  проходящей через его центр масс перпендикулярно к стержню (Рис. 4). Выделим на расстоянии х от оси вращения элемент стержня бесконечно малой толщины d x.
проходящей через его центр масс перпендикулярно к стержню (Рис. 4). Выделим на расстоянии х от оси вращения элемент стержня бесконечно малой толщины d x. () Учитывая, что элементы массы dm попарно симметричны относитель-
() Учитывая, что элементы массы dm попарно симметричны относитель- ()
() – масса стержня, то окончательно для тонкого стержня
– масса стержня, то окончательно для тонкого стержня (33)
(33) Определим момент инерции диск или цилиндра радиусом R, высотой h и массой m относительно его геометрической оси, параллельной образующей. Выделим цилиндрический слой бесконечно малой толщины dr и радиусом r. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя
Определим момент инерции диск или цилиндра радиусом R, высотой h и массой m относительно его геометрической оси, параллельной образующей. Выделим цилиндрический слой бесконечно малой толщины dr и радиусом r. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя .
.
 ,
, 
 (36)
(36) (31)
(31) (32)
(32) , (33)
, (33)
 (34)
(34) а) тонкий однородный стержень.
а) тонкий однородный стержень.

 , то окончательно
, то окончательно  (33)
(33) Выделим цилиндрический слой бесконечно малой толщины dr и радиусом r. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя
Выделим цилиндрический слой бесконечно малой толщины dr и радиусом r. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя .
.
 ,
, 
 (36)
(36) , (33)
, (33) к стержню и проходящей через его центр масс.
к стержню и проходящей через его центр масс. где J0 – момент инерции тела относительно оси через центр масс, d - расстояние между осями. Например, для стержня, если ось вращения проходит через его конец (рис.1):
где J0 – момент инерции тела относительно оси через центр масс, d - расстояние между осями. Например, для стержня, если ось вращения проходит через его конец (рис.1):


