
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение математической модели задачи.Содержание книги
Поиск на нашем сайте
N- число городов. Cij,I,J=1..N-матрица затрат, где Cij-затраты на переход из I – го города в j-й. Xij-Матрица переходов с компонентами: Xij=1, если коммивояжер совершает переход из I – го города в j – й, Xij=0, если не совершает перехода, где I,J= 1..N и I< >J
Критерий:
Ограничения имеют вид:
Доказательство, что модель (1-4) описывает задачу о коммивояжере. Условие (2) означает, что коммивояжер из каждого города выезжает только один раз; условие (3) – вывезут в каждый город только один раз; условие (4) – обеспечивает замкнутость маршрута, содержавшего N городов, и не содержащего замкнутых внутренних петель. Рассмотрим условие (4). Применим метод доказательства от противного, то есть предположим, что условие (4) выполняется для некоторого под цикла T из R городов, где R<N. Сложив все неравенства (4) вдоль этого под циклом получим
Так как
то N-R≤(N-1), где R<N, R≠0. Следовательно не существует замкнутого под цикла с числом городов меньшем N. Покажем, что существует Uij которое для замкнутого цикла начинающегося в некотором начальном пункте, удовлетворяют условию (4). При всех Xij (J – й город не посещается после i-го), а (4) имеем Ui-Uj≤N-1, что допустимо в силу произвольных Ui и Uj. Пусть на некотором R-ом шаге i-й город посещается перед j-м, то есть X и J=1. В силу произвольности значений Ui и Uj положим Ui-R, а Uj=R-1, тогда из (4) имеем: Ui-Uj N- Xij≤R-(R-1)+N=N+1 Итак, существуют такие конечные значения для Ui и Uj, что для маршрута, содержащего N городов, условие (4) удовлетворяется как неравенство или строгое равенство. А, следовательно, модель (1-4) описывает задачу о коммивояжере.
Рассмотрим реализации метода ветвей и границ для решения задачи о коммивояжере.
Верхняя строка и левый столбец, выделенные затемнённым фоном, содержат номера вершин графа; символ
Подсчитаем фи(Г) в нашем примере. Для этого выполним приведение матрицы весов; сначала- по строкам: Таблица 1
Результат приведения по строкам:
Таблица 2
Определим константы по столбцам: Таблица 3
результат проведения матрицы:
Сумма констант приведения фи(Г)=2+4+4+4+3+1+1=19
Обозначим матрицу через Ml найдём в ней самый длинный путь. Для этого запишем матрицу ещё раз, указывая рядом с каждым нулём в степени его длинну: Таблица 5
Ml
Самым длинным оказывается ноль в клетке (1,5). Следовательно, множество Г разбивается на Г(1,5) В следующей матрице перед вычеркиванием строки и столбца, заменяем в ней на
Таблица 6
Переведём теперь эту матрицу: Таблица 7
Это – матрица Ml,l; сумма констант приведения здесь равна 2, поэтому Фи(1,5)=19+2=21 Для М1,2 заменяем на Таблица 8
Это матрица М1.2; сумма констант последнего приведения равна 3, так что фи{1,5}=19+3=22. Следовательно, дальнейшей разработке подвергается множество Г{1,5}. Вот нулей матрицы М1,1 (они указаны в скобках): Таблица 10
Самым длинным является ноль с номером (5,4) теперь следует рассматривать множества Г(1,5)(5,4) и Г(1,5){5,4}. Обратимся к первому из них. Перед тем как в очередной матрице вычеркнуть строку и столбец, в ней надо заменить на Следовательно, клетки с номерами (5,2),(5,3) и (4,1) надо заполнить символом Таблица 11
Приведение этой матрицы: Таблица 12
Для оценочной функции: Фи(1,5)(5,4)=21+2=23. Матрица для множества Г(1,5){5,4}:
Таблица 13
Таблица 14
Оценочная функция фи(1,5){5,4}=21+2=23. Следовательно, дальнейшей разработке Г{1,5}{5,4}Взвешиваем нули: Таблица 15
Выбираем любую из соответствующих клеток; для клетки (2,1). Теперь речь пойдёт о множествах Г{1,5}{5,2}{2,1} и Г{1,5}{5,4}{2,1}. Как и в преждней матрице вычеркнуть строку и столбец, в ней надо заменить на
Таблица 16
Приведём эту матрицу:
Получаем для оценочной функции: фи{1,5}{5,4}{2,1}=23+0=23.
Таблица 18
Приведение этой матрицы даёт: Таблица 19
Для оценочной функции:фи{1,5}{5,4}{2,1}=23+0=23. Получилось, что для дальнейшей разработки можно брать Г{1,5}{5,4}{2,1}.В первом случае уже получена матрица размером 2х2; её нулевые клетки дают рёбра, которые с найденными ранее составляют обход коммивояжера, причём вес этого обхода равен значению оценочной функции-23. Вот этот обход: (1,5)(5,4)(2,1)(3,2) или 1→5→4→3→2→1. Найденный рекорд на самом деле является искомым оптимумом, потому что значения оценочной функции на всех оборванных ветвях(на границах) больше или равны весу рекорда.
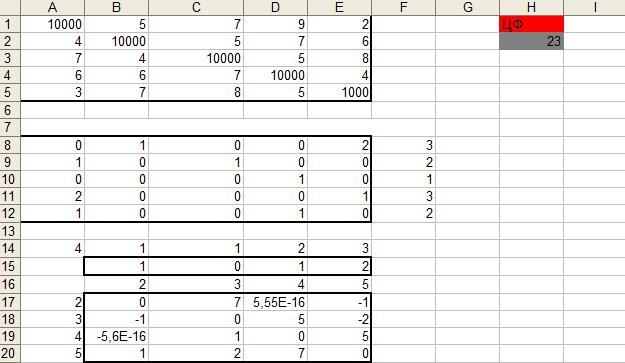
Вид электронной таблицы, созданной для решения задачи, представлен на рис. 1. Значения переменных xij располагаются в блоке А1:Е5. В данном блоке ячейки, расположенные по диагонали обнулены (пункт назначения не может быть одновременно пунктом прибытия). Целевая функция расположена в ячейке H2.
Рис.1
На рис. 2 в ячейках с А8:Е12 находятся функции переменных которые нужны для того, чтобы найти целевую функцию. Найдём сумму по каждому столбцу по формуле: (=СУММ(A8:A12)) эта формула используется в сумме последующих столбцах. Так же найдём сумму для строки по формуле: (=СУММ(A8:E8)) которая используется в последующих строчках. Рис.2 На рисунке 3 ограничения находятся в строке В15:Е15. Формулы для ограничения находятся в ячейках В17:Е20
На рис. 4 находим сумму целевой функции по формуле показанной на рисунке.
Рис.4
Через сервис открываем Поиск решения задав ограничения и параметры выводим целевую функцию. Рис.5
Рис.6
ЗАКЛЮЧЕНИЕ В данной курсовой работе были рассмотрены основные теоретические вопросы по задаче коммивояжера. Приведено решение вручную задачи методом ветвей и границ (методом Литтла). Приведено решение задачи в среде MicroSoft Office Excel 2000. Изучено практическое применение задачи коммивояжера в экономике и производстве.
1. Вентцель Е.С. Исследование операций: задачи, принципы, методология. – М.: Высшая школа, 2004. – 208 с. 2. Исследование операций в экономике/ Под ред. Кремера Н.Ш. – М.:ЮНИТИ, 2004. – 407 с. 3. Конюховский П.В. Математические методы исследования операций в экономике. Краткий курс. – СПб.: Питер, 2002. – 208 с. 4. Просветов Г.И. Математические методы в экономике: Учебно-методическое пособие. – М.: Издательство РДЛ, 2004. – 160 с. 5. Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач. – М.: Вузовский учебник, 2004. – 144 с. 6. Костевич Л.С. Математическое программирование: Информационные технологии оптимальных решений. – Мн.: Новое знание, 2003. – 424 с. 7. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986. – 319 с.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.250.65 (0.008 с.) |



 (2)
(2) (3)
(3) (4)
(4)

 2.3 Решение задачи вручную.
2.3 Решение задачи вручную.


 после этого приводим полученную матрицу:
после этого приводим полученную матрицу: таблица 9
таблица 9 Результат её приведения:
Результат её приведения: Таблица 17
Таблица 17 2.4 Решение задачи в Excel
2.4 Решение задачи в Excel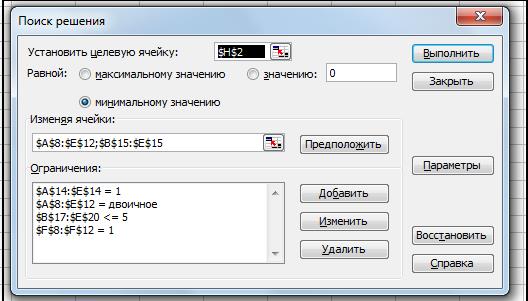
 По результатам поиска решения найден ответ задачи: (см. рис. 6).
По результатам поиска решения найден ответ задачи: (см. рис. 6).

 Список литературы
Список литературы


