
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фазовые переходы первого и второго рода. Условия устойчивости и равновесия.Содержание книги
Поиск на нашем сайте
Фазой называется макроскопическая физически однородная часть вещества, отделённая от остальных частей системы границами раздела, так что она может быть извлечена из системы механическим путём. В системе может быть несколько жидких или твёрдых фаз, но она не может содержать более одной газообразной фазы, т.к. все газы смешиваются между собой. Фазовое равновесие между любыми фазами 1 и 2 не есть статическое состояние, в котором полностью прекратились фазовые превращения, а характеризуется равенством средних скоростей двух взаимно противоположных процессов: превращение фазы 1 в 2 и обратно. Для осуществления перехода из жидкой фазы в газообразную системе необходимо сообщать теплоту без изменения температуры системы. Эта теплота идёт на изменение фазового состояния вещества и называется теплотой фазового превращения, или скрытой теплотой перехода.
Рассмотрим бесконечно малый цикл Карно, изотермами в котором являются состояния двухфазной системы при температурах В тройной точке одновременно находятся в равновесии газ, жидкость и твёрдое тело. Для воды: В качестве объекта исследования возьмем микроскопически малое изменение Т/Д состояния (из 1→2): Отличие Для квазистатических процессов (перехода) Для не являющихся квазистатическими: Условие равновесия для различного рода зафиксированных неравновесных систем: а) адиабатически изолированная система:
здесь
– необходимое условие экстремума (усл-е Т/Д равновесия), а
б) система в термостате:
в) система, выделенная вообр. стенками: при
г) система под поршнем:
Т/Д равновесие наступает при Условие равновесия: Условие устойчивости:
а) устойчивость к тепловому воздействию на систему. Рассмотрим через вариант б)
Общее условие равновесия фаз в ТД системах.
Вернёмся к 1-компонентной (только вода, к примеру) 2-х фазной системе (жидкость-газ). Определение: если
Отличия: 1) скрытая теплота ф.п. 1→2 отлична от, 2) скачок удел объёмов
Пример: кипение, испарение, плавление твердого тела, возгонка, переход одной кристалл модификации в др. Уравнение кривой фазового равновесия:
Фазовые переходы 2 рода. Определение: В
т.е. переходы с нулевой
Пример: переход проводника из сверхпроводящего состояния в нормальное.
Отличия: есть скачок некоторых величин:
Уравнения Эренфеста:
Явления переноса. Теплопроводность: перенос теплоты. Теплопроводность не зависит от давления и увеличивается пропорционально корню квадратному из температуры. В этом случае Коэффициент теплопроводности:
Замечания: 1) Диффузия: движение вещества компонент, составляющих фазу, связанное с отклонением плотности системы. Коэффициент диффузии: Замечания: 1) Вязкость: возникновение сил трения в газах и жидкостях обусловлено процессом переноса импульса упорядоченным движеним молекул. Быстрее движущийся слой замедляется, а медленнее движущийся – ускоряется. Пусть
Замечания: 1) Потоки всех величин являются алгебраическими. Их знак зависит от направления оси Во всех явлениях переноса направления плотностей потоков противоположны градиентам соответствующих величин. Это означает, что потоки всегда направлены в сторону уменьшения величин
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.152 (0.006 с.) |

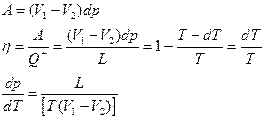 Фазовые переходы первого рода: Фазовые переходы с выделением или поглощением скрытой теплоты. Отличительной особенностью фазовых переходов первого рода является скачкообразное изменение удельной внутренней энергии и связанных с ней величин в точке перехода, и следовательно, наличие скрытой теплоты перехода.
Фазовые переходы первого рода: Фазовые переходы с выделением или поглощением скрытой теплоты. Отличительной особенностью фазовых переходов первого рода является скачкообразное изменение удельной внутренней энергии и связанных с ней величин в точке перехода, и следовательно, наличие скрытой теплоты перехода. и
и  .
.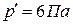 ,
,  .
. мало.
мало.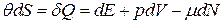 .
. (*).
(*). , из (*) получаем
, из (*) получаем  ,
, – энтропия Т/Д потенциала,
– энтропия Т/Д потенциала,  – внутренняя энергия,
– внутренняя энергия,  – объём,
– объём,  – число частиц,
– число частиц,  – химический потенциал,
– химический потенциал,  обозначает вариацию.
обозначает вариацию. – энтропия возрастает до
– энтропия возрастает до 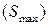 – состояния Т/Д равновесия, т.е.
– состояния Т/Д равновесия, т.е.
 – условие максимума экстремума и одновременно условие устойчивости равновесного состояния.
– условие максимума экстремума и одновременно условие устойчивости равновесного состояния. .
. 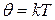 – температура; из (*):
– температура; из (*):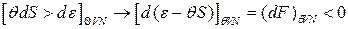 .
. – свободная энергия, Т/Д потенциал, т.е. течение неравновесных процессов в системе «термостат» сопровождается уменьшением её свободной энергии, где
– свободная энергия, Т/Д потенциал, т.е. течение неравновесных процессов в системе «термостат» сопровождается уменьшением её свободной энергии, где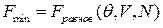 и
и  ,
,  .
.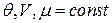
 , т.к. из (*):
, т.к. из (*): .
. – большой Т/Д потенциал
– большой Т/Д потенциал 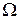 .
. . Из (*) получаем:
. Из (*) получаем: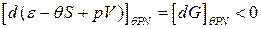 .
. ,
,  – Т/Д потенциал Гиббса.
– Т/Д потенциал Гиббса.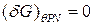 ,
, .
. . Пример устойчивости:
. Пример устойчивости: дают
дают  – усл-е уст-ти к нагреванию системы под поршнем.
– усл-е уст-ти к нагреванию системы под поршнем. и
и  аналитически не получить, поэтому зависимость
аналитически не получить, поэтому зависимость  снимают эмпирически. Однако
снимают эмпирически. Однако  и
и 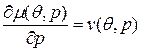 – можно измерить экспериментально.
– можно измерить экспериментально. и
и 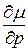 имеют для разных фаз в точках
имеют для разных фаз в точках  разные значения, то такой фазовый переход называется переходом 1-го рода.
разные значения, то такой фазовый переход называется переходом 1-го рода. – скачок
– скачок  .
. .
.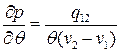 .
. определяется 3-мя усл-ми:
определяется 3-мя усл-ми: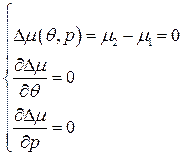
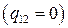 скрытой теплотой плавления и без скачка плотности – такие переходы называются фазовыми переходами 2-го рода.
скрытой теплотой плавления и без скачка плотности – такие переходы называются фазовыми переходами 2-го рода.
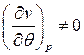 – коэффициент теплового расширения
– коэффициент теплового расширения – коэффициент упругости.
– коэффициент упругости.
 .
. ,
,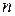 – концентрация,
– концентрация,  – молярная теплоёмкость (
– молярная теплоёмкость ( – число степеней свободы),
– число степеней свободы),  – длина свободного пробега.
– длина свободного пробега. ,
,  не зависит от давления; 2)
не зависит от давления; 2)  .
.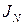 – плотность диффузионного потока (кол-во вещ-ва, проходящего перпендикулярно единице площади в ед. времени).
– плотность диффузионного потока (кол-во вещ-ва, проходящего перпендикулярно единице площади в ед. времени).  – закон Фика.
– закон Фика. ,
, 
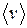 – средняя скорость.
– средняя скорость. ,
, 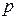 – давление; 2)
– давление; 2)  .
. . Кинематическая вязкость – динамическая вязкость, отнесённая к плотности.
. Кинематическая вязкость – динамическая вязкость, отнесённая к плотности. направлена вдоль градиента
направлена вдоль градиента 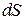 после последнего столкновения, равно 2<l>3.
после последнего столкновения, равно 2<l>3.  – импульс, передаваемый в единицу времени от слоя к слою через единицу поверхности, т.е. плотность потока импульса.
– импульс, передаваемый в единицу времени от слоя к слою через единицу поверхности, т.е. плотность потока импульса.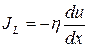 ,
,  – скорость движения газа как целого.
– скорость движения газа как целого.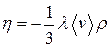 .
. не зависит от давления; 2)
не зависит от давления; 2)  .
. ,
, 


